Physicist: Straight.
In fact, in mathematics the “curvature” of a curve is usually defined as the “reciprocal of the radius of the osculating circle”. This is fancy talk for: fit a circle into the curve as best you can, then measure the radius of that circle, and flip it over.
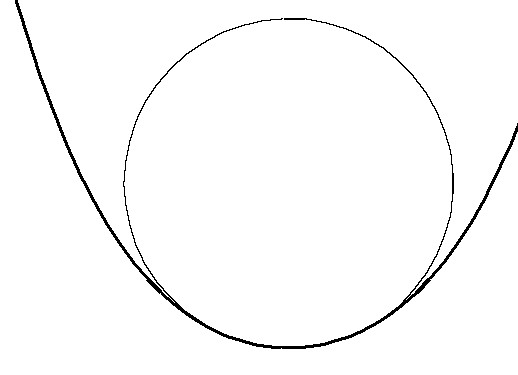
At any given point the osculating (or "kissing") circle is the circle that fits a curve as closely as possible.
It makes sense; a smaller circle should have a higher curvature (it’s turning faster) but it has a smaller radius, R. So, use 1/R, which is big when R is small, and small when R is big. There are some more technical reasons to use 1/R (like that you can apply it directly to calculating the centrifugal force on a point following that path, or that it gives rise to the entirely kick-ass Descartes’ theorem), but really it’s just one of the more reasonable definitions.
So, just working with the standard definition, you say: the curvature of a circle is 1/R, if I let the radius become infinite, the curvature must go to zero. Zero curvature means no bending of any kind. Must be a line.
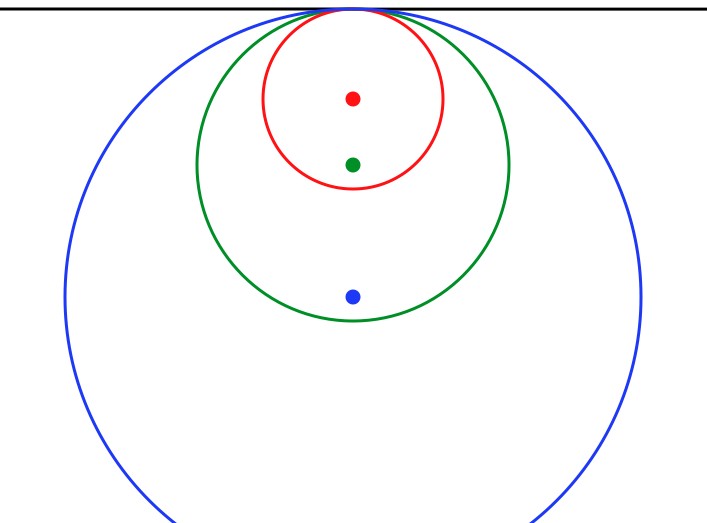
Nail down the edge of a circle. As the center gets farther and farther away, the radius gets larger, and the curvature gets smaller. When the "circle is centered at infinity" the curvature drops to zero, and the edge becomes a straight line (black).
Old school topologists get very excited about this stuff.
Say you have two lines on a plane. They’ll always intersect at exactly one point, unless they’re parallel in which case they’ll never intersect at all. But the Greek Geometers, back in the day, didn’t like that; they wanted a more universal theorem. So they included the “line at infinity” with their plane, and created the “projective plane”. In so doing they created a new space where every pair of straight lines intersect at one point, no matter what.
To picture this, imagine the ground under your feet as the plane and the horizon as the line-at-infinity.
The tracks are parallel, so they'll never meet. But, they look like they meet at the horizon. So why not (mathematically speaking) "include" the horizon and define that as the place where the tracks meet?
Parallel lines meet at two points on the horizon (in opposite directions). So the line at infinity is weirdly defined with opposite points on the horizon being the same point. Mathematicians would say “antipodal points are identified”. In the projective plane two lines always meet at one point.
Notice that east-west parallel lines meet at the east-west point on the line at infinity, and north-south parallel lines meet at the north-south point at infinity. So you do need the entire horizon, not just a single “far away point”. A single point would yield the Riemann sphere, which is also good times.
Back to the point. If you think about circles in this new-fangled projective plane, one of the first questions that comes to mind is “what happens if the circle includes a point on the line at infinity?”.
No matter how big the circle is, or where its center is, the whole thing will always be in the plane (not all the way out to the line at infinity). If the circle does have a point on the horizon, then you’ll find that the center also has to be at infinity (if it’s in the plane, then it’ll be closer to some points on the circle than others, but the center point is the same distance to every point on the circle). Specifically, the center will be on the line at infinity exactly 90° away from where the circle intersects the line.
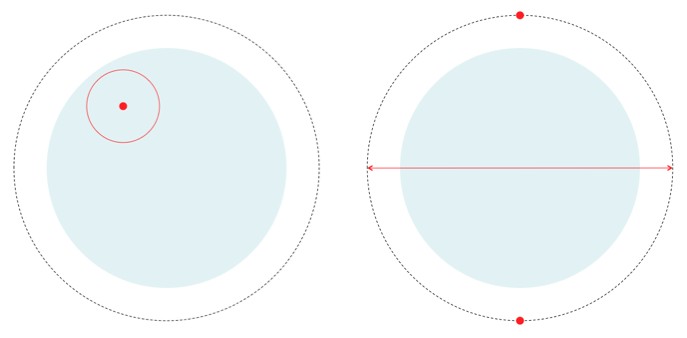
The projective plane, which includes the usual infinite plane (light blue) and the line at infinity (dashed line), and two examples of circles. Note that, although the plane is infinite, the line at infinity wraps around it in the same way that the horizon would still wrap around you even if the Earth were flat and infinite (this is an abstract picture). Left: a circle and its center in the in the ordinary plane. Right: a circle that passes through the east-west point on the line-at-infinity. Its center is at the north-south point on the line-at-infinity.
This agrees surprisingly well with the intuition behind the more colorful circle picture above. Science and math truly are a beautiful tapestry of interconnections and nerding right the hell out.
Pingback: Fourth Linkfest
I could be misunderstanding, but given the edge of a circle centered at infinity has zero curvature, so is straight, and that any straight line can be described this way too. What defines a circle as a circle? Do circle exist as separate and distinct from lines?
Would two circles centered at two different points at infinity intersect at only one point? or an infinite number of points?
The projective plane is one of a few different ways of looking at the situation (there’s no “correct” one). Having a center at infinity dictates the direction of the line, so two “circles” with different centers on the line at infinity would be two lines that cut across the plane at different angles. They’d intersect at one point (somewhere in the plane).
Circles and lines are different in the ordinary “Cartesian” plane, nearly the same in the projective plane, and exactly the same in the “compactified” plane (the Riemann sphere). It’s just a matter of picking your topological poison.
I prefer the projective plane because it’s easier to picture. Most mathematicians prefer the Riemann sphere (a point at infinity instead of a line) because it makes complex (as in “square root of -1″) mathematics easier. But, you know, whatever works.
Another perspective.
(Real) projective space is the quotient of the sphere by antipodal identification, so when you’re talking about a curve in the projective plane, you’re really talking about a curve on a sphere that is the same reflected through the origin. In particular, this is true of great circles. So great circles on the sphere become lines through the origin of the projective planes.
But the Greek Geometers, back in the day, didn’t like that; they wanted a more universal theorem. So they included the “line at infinity” with their plane, and created the “projective plane”. In so doing they created a new space where every pair of straight lines intersect at one point, no matter what.
The Greeks invented the projective plane? I thought the Greeks didn’t like infinity and that projective geometry came much later.
(It makes me sad to think that i’ll probably never see your reply, because I’ll probably forget to visit this page again in a few days. have you ever considered making it possible for commenters to receive future comments via email?)
Not intended to be a factual statement.
This is the sort of thing that follows on the heels of Euclid’s postulates. Somebody back then must have been pondering this stuff.
Basically, the notions of the projective plane (the horizon, lines and circles having a lot in common, …) goes way back. But no, you’re right, the Greeks definitely didn’t come up with the rigorous definition and formalism of the modern projective plane. That was just in the last couple centuries.
any question containing any reference to “infinity” is incoherent, and asking questions that actually mean something ought to be encouraged.
the entire line taken by “the Physicist” misses a critical point. infinity is not a number, and division by infinity, as an immediate consequence, is as internally consistent an idea as division by purple.
the limit of the sequence of curvatures may be zero, but you’ve some interesting work ahead of you, to show the sequence of curves on that diagram converges to anything, let alone that the curvature of the limit is the limit of the curvatures.
Infinity definitely isn’t a number, but in this context (trying not to get too pedantic) I approached it in terms of limits in the first half, and in terms of topological closure in the second. That is, redefining the space to include infinity (“numberizing” it). Both of those approaches are totally kosher.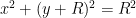
. Solving for y we find: 
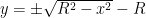. These solutions correspond to the upper and lower halfs of the circle. The lower half doesn’t converge, but the upper half does. Holding x fixed, and allowing R to become arbitrarily large:
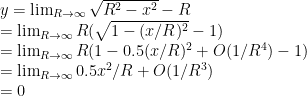
As for the circles approaching a line I figured a picture was best, since the strictly mathematical approach is a bit dry. That being said:
This set of circles, indexed by the parameter R, are defined as
So, at every point x along the line the y value of the circle converges to zero. The lower half doesn’t converge at all (unless you change the topology).
The short answer to this question is curved, that is, if the question made sense in the first place.
Consider any tangent line to a circle. It contacts the circle at precisely one point. For the edge of a circle to ever be straight, it would have to contact the tangent line at more than one point. Can this ever happen? No, and here is why:
Take any circle of radius R where R is a real number. Any line perpendicular to the radius will contact the edge of the circle once.
Double R, and the tangent line still only contacts the edge once.
Double R again, and we get the same result.
Repeat this again and again and again…We still get one contact point
We could define this as a function: The number of contact points of a tangent line to a circle as f(R)=1. The limit of this function as it approaches infinity is still going to be 1.
Absolutely!
Given that definition, the edge will always be curved. But it doesn’t seem like the most intuitive definition.