Q: Why is the integral/antiderivative the area under a function?

Physicist: If you’ve taken calculus, then at some point you learned that to find the area under a function (generally written ) you need to find the anti-derivative of that function.  The most natural response to these types of theorems is “wait… what?… why?”.

This theorem is so important and widely used that it’s called the “fundamental theorem of calculus”, and it ties together the integral (area under a function) with the antiderivative (opposite of the derivative) so tightly that the two words are essentially interchangeable.  However, there are some mathematicians who may take issue with mixing up the two terms.

It comes back (in a roundabout way) to the fact that the derivative of a function is the slope of that function or the “rate of change”.  In what follows “f” is a function, and “F” is its anti-derivative (that is: F’ = f).

Intuitively: Say you’ve got a function f(x), and the area under f(x) (up to some value x) is given by A(x).

Then the statement “the area, A, is given by the anti-derivative of f” is equivalent to “the derivative of A is given by f”.

In other words, the rate at which the area increases (as you slide x to the right) is given by the height, f(x).

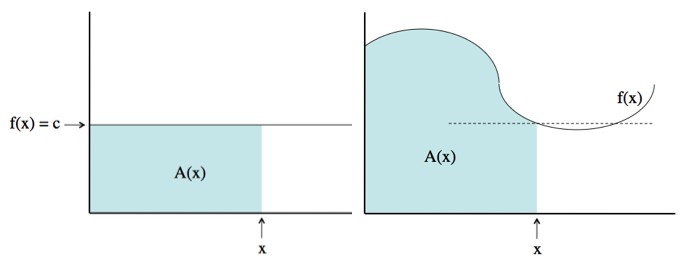
For a constant function the area is given by A=cx, and the rate of increase (the amount that the area increases if x increases by 1) is c. Whether or not the function moves around makes no difference. From moment-to-moment the rate of increase is always equal to the height (the value of f).

For example, if the height of the function were 3, then, for a moment, the area under the function is increasing by 3 for every 1 unit of distance you slide to the right.  Keep in mind that the function can move up and down as much as it wants.  As far as the function “knows”, at any particular moment it may as well be constant (dotted line in picture above).

So if the height of the function (which is just the function) is the rate at which the area changes, then f is the derivative of the area: A’=f.  But that’s exactly the same as saying that the area is the anti-derivative of the function.

Mathematically: There’s a theorem called the mean value theorem that states that if you have a “smooth” function with no sudden bends or kinks, then over any interval the derivative will be equal to the average slope at least once.  This needs a picture:

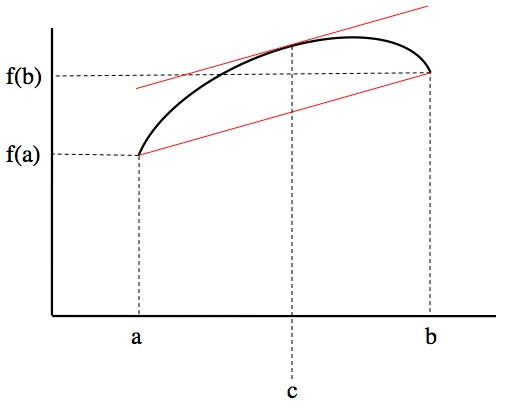
Given a smooth function f, there's a point c where the function has the same slope as the overall average slope.

More precisely, if you have a function on the interval [A,B], then there’s a point c between A and B such that .  You can just as easily write this as or (since F’ =f).

So if you drive 60 miles in one hour, then at some instant you must have been driving at exactly 60 mph, even though for almost the entire trip you may have been traveling much faster or much slower than 60 mph.

Keep that stuff in the back of your mind for a moment, and ponder instead how to go about approximating the area under a function.

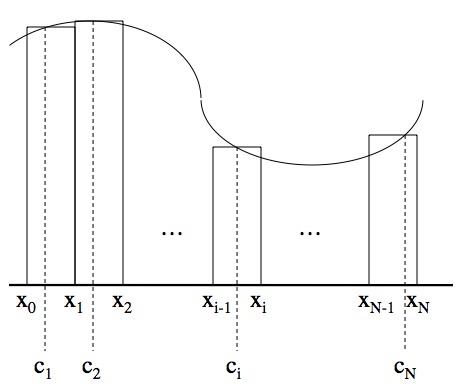
You can approximate the area under a function by dividing it up into a whole lot of tiny rectangles. The area of each is the width times the height, where the height is any value of f in that particular interval. Choosing different values does change the area of that rectangle, but it turns out that that doesn't matter.

You can divide up the area between x=A and x=B under a function by putting a mess of rectangles under it.   Divide up the interval [A,B] by picking a string of points x₀, x₁, x₂, …, x_N, and use these as the left and right sides of your rectangles (and set x₀=A and x_N=B).

The point, c_i, that you pick in between each x_i-1 and x_i is unimportant.  To get the exact area you let N, the total number of rectangles, go flying off to infinity, and you’ll find that the highest value of f and the lowest value of f in each tiny interval gets squeezed together.

So, why not choose a value of c_i so that in each rectangle you can say ?

Holy crap!  The area under the function (the integral) is given by the antiderivative!  Again, this approximation becomes an equality as the number of rectangles becomes infinite.

As an aside (for those of you who really wanted to read an entire post about integrals), integrals are surprisingly robust.  That is to say, if your function has a kink in it (the way |x| has a kink at zero, for example) then you can’t find a derivative at that kink, but integrals don’t have that problem.  If there’s a kink or even a discontinuity; no problem!

You can just put the edge of a rectangle at the problem point, and then ignore it.  In fact, think of (almost) any function in your head…  You can take the integral of that.  It may have an infinite value, or something awful like that, but you can still take the integral.

To make a function that can’t be integrated you have to make it infinitely messed up.  Mathematicians live for this sort of thing.  There is almost nothing in the world they enjoy more than coming up with ways to break each other’s theories.  One of the classic examples is the function

Over any interval you pick, f still jumps around infinitely often, so the whole “things will get better as the number of rectangles increases” thing can never get off the ground.  There are fixes to this, but they come boiling and howling up out of the ever-darker, stygian abyss that is measure theory.