Physicist: Math. Math all over.
A picture of a 3D object is a “projection” of that object onto a 2D page. Projection to an artist means taking a picture or drawing a picture. To a mathematician it means keeping some dimensions and “pancaking” others.
So when you take a picture the “up/down” and “left/right” dimensions are retained, but the “forward/back” dimension is flattened. Mathematicians, being clever, have formalized this into a form that is independent of dimension. That is, you can take an object in any number of dimensions and “project out” any number of dimensions, until it’s something we can picture (3 or fewer dimensions).
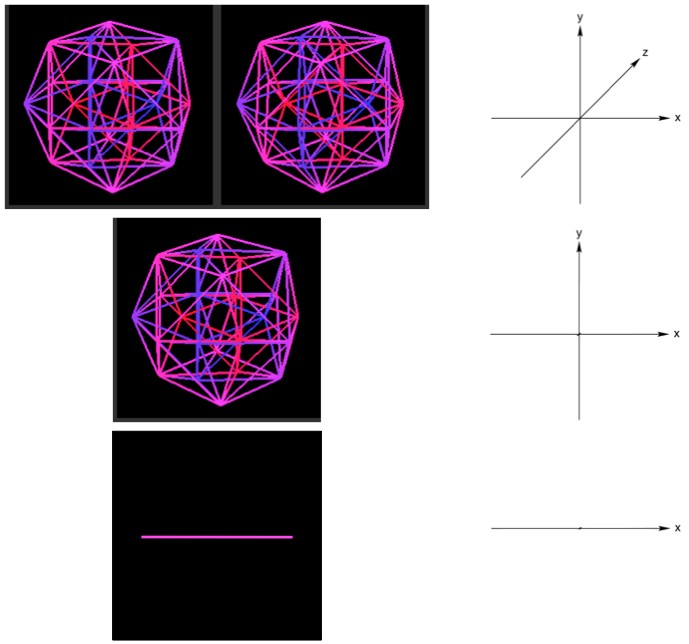
Top: An object in 3 dimensions. To see it, cross your eyes by looking “through” the screen until the two images line up. Middle: By “projecting out” the z axis (toward/away) the object is collapsed into two dimensions. This is what cameras do. Bottom: By projecting out the y axis (up/down) the object is collapsed again into 1 dimension. This is akin to what a 2D camera would see, photographing from below.
We’re used to a 3D-to-2D projection (it’s what our eyeballs do). A 4D-to-2D projection, like in the picture above, would involve 2 “camera/eyeball like” projections, so it’s not as simple as “seeing” a 4D object.
As for knowing what a 4D, 5D, … shape is, we just describe its properties mathematically, and solve. It’s necessary to use math to describe things that can’t be otherwise pictured or understood directly. If we had to completely understand modern physics to use it, we’d be up shit creek. However, by describing things mathematically, and then following the calculations to their conclusions, we can get a lot farther than our puny minds might otherwise allow.
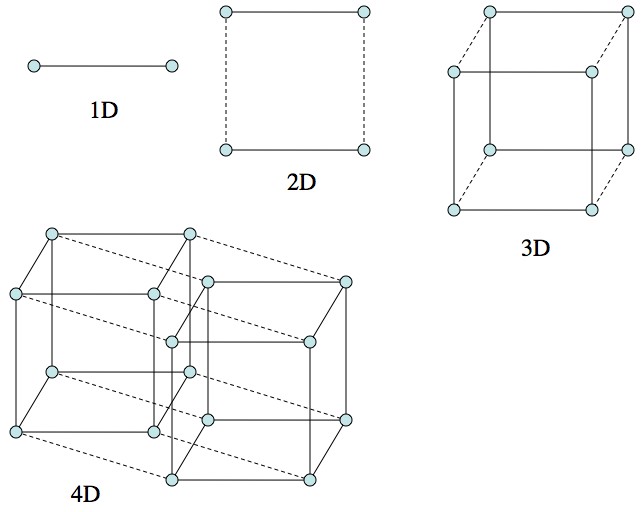
Lines, squares, cubes, hyper-cubes, hyper-hyper-cubes, etc. all follow from each other pretty naturally. The 4D picture (being 4D) should be difficult to understand.
For example, to describe a hypercube you start with a line (all shapes are lines in 1D).
To go to 2D, you’d slide the line in a new direction (the 2nd dimension) and pick up all the points the line covers. Now you’ve got a square.
To go to 3D, you’d slide the square in a new direction (the 3rd dimension) and pick up all the points the square covers. Cube!
To go to 4D, same thing: slide the cube in the new (4th) direction. The only difference between this and all the previous times is that we can no longer picture the process. However, mathematically speaking, it’s nothing special.
Answer gravy: This isn’t more of an answer, it’s just an example of how, starting from a pattern in lower dimensions, you can talk about the properties of something in higher dimensions. In this case, the number of lines, faces, etc. that a hyper-cube will have in more than 3 dimensions.
Define 
Now define 
For example, by looking at the square (picture above) you’ll notice that 
The “slide, connect, and fill in” technique can be though of like this: when you slide a point it creates a line, when you slide a line it creates a square, when you slide a square it creates a cube, etc. Also, you find that you’ll have two copies of the original shape (picture above).
So, if you want to figure out how many “square pieces” you have in a D-dimensional cube you’d take the number of squares in a D-1 dimensional cube, double it (2 copies), and then add the number of lines in a D-1 dimensional cube (from sliding).
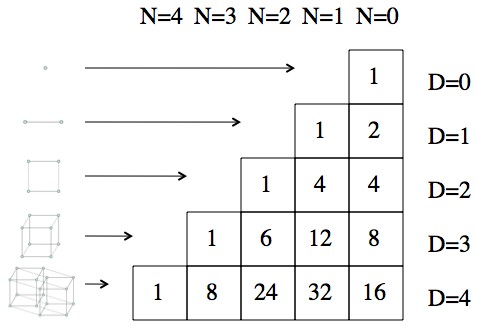
The values of e_N(D) arranged to make the pattern clearer. You can use the pattern to accurately predict what the cube in the next dimension will be like.
It’s neither obvious nor interesting how, but with a little mathing you’ll find that 
In order to actually do meaningful math in dimensions higher than three, you have to make your peace with being entirely unable to do more than (a) draw crude two- or three-dimensional visualizations or (b) draw vague scribbly conceptual pictures.
(It’s actually kind of funny to watch topologists “prove”* things. Spaces (even spaces where “dimension” doesn’t even make sense) become boxes, or lines if you’re taking products or suspending. Embeddings become squiggles in blobs. Suspensions? Pointy spheres. Taking a quotient? Scribble in the subspace being identified. It goes on and on.)
* These things all have precise definitions. The pictures merely suggest the actual proofs, which of course are always left as an exercise.
On the hypercube, are the angles also 90 degrees, like in a regular cube and in a square?
Assuming yes: so there are 4 sides which all are perpendicular to each other?
Assuming no: what are the angles between the sides? can they be measured?
Yes.
In an N-dimensional cube each corner is the intersection of N mutually perpendicular sides.
The fourth dimension is not at all hard to conceptualize from the drawing. If one is used to seeing three dimensional objects move in any of the three dimensions, and can remember that at time t the 3D object was here, and now at time t+1, the 3D object is now THERE, you basically have it.
Intuitively conceptualizing the fifth dimension from the first four is the tricky part because we have no intuitive frame of reference. I imagine it would be akin to watching a 3D cube move in one direction, while its 6 shadows on the sides of a larger box containing it from the six coordinate light sources also move, and you would see the lines of the shadow persisting from each opaque line itself to the walls of the cube containing the 3D cube.
Of course, this is mere intuition.
Pingback: Paris | Yep.
hi : i think that the hypercube above is just an other 3D shape , and i believe that in 3d world we can assume how 4D SHAPE will look like , if we take on consedairation other condition , …..
thanks
What do You mean by N-Dimensional?
“N-dimensional” is just a short hand way of saying “any dimension”. Just replace “N” with any number.
I had the following problem in Dr. Strang’s Linear Algebra book:
Problem: “How many corners does a cube have in 4 dimensions? How many 3D faces? How many edges? A typical corner is (0,0,1,0). A typical edge goes to (0,1,0,0).”
I looked at the problem for 60 minutes and only solved the number of corners. Although I have taken much math as a chemical engineer, problems such as this, fundamental problems in math, have always given me great difficulty. I guess that is why I earned a BS in chemical engineering instead of a PhD.
In the back of Dr. Strang’s book, the answer to the problem says the number of 3D faces is “4 x 2 = 8.” I have no idea where he came up with that solution. From looking at hypercubes on the internet, something I could not visualize myself, I see that a 4D cube is often drawn as 2 3D cubes. Still, I don’t believe that is where the “2” came from if considering the “4” coming from 4 dimensions.
To be honest, I don’t see how you got your faces and edges either. I do know that I would have never come up with your mathematical explanation as an answer to Dr. Strang’s problem.
I wish I had such skills.
Hello,
I see some of the patterns now as I look at your well organized data. I have not done math in a while, but I see that my organizational skills have gone far south. Sadly, I now suffer from 1991 Gulf War Illness and schizoaffective disorder and each causes cognitive problems. Stress affects me horribly too.
As I look at your data, I can see that I would have found the pattern that shows why Dr. Strang gave a solution of “4 x 2 = 8”. Also, I had already figured out the number of corners. I believe I see the pattern that allows one to predict 24, 2D faces as well. I see the “diagonal” patterns in your data organization, but I don’t know if I “see” the patters because I already know the answer.
It frustrates me to do so poorly on a problem. Like I said, it is likely why I am a BS chemical engineer than a PhD. By the way, I actually did well in my math classes and averaged A’s. I cannot explain it, but problems like this always kicked my butt. I believe it is because I have always had an organizational problem. Also, I now have a problem with concrete thinking, which is a cognitive symptom of schizophrenia.
Thanks for the education. The only possible pattern that I do not see is the one that produces 32. That is assuming my other recognized patterns are correct.
to work the hype cube out. once must use a ref points. i see your charts .would it be more eazy just to use a hologram for the cube. then run it like a movie to see it movement of the cube it take a lot of confustion out of the matter.? Also i believe you can use the cube make a ref point. or door into time travel . From my notes of course john
I’m just a high school student but I have been thinking.
A 1D shape has 0 dimensional faces, a 2D shape has 1 dimensional faces and a 3D dimensional shape has 2 dimensional faces. Is not a 4D shape suppose to have 3 dimensional faces?
The images above seem to have 2 dimensional faces.
I believe we live in the 4th dimension. We perceive the 4th dimension as time. It is basically a 3d object, only dynamic, or changing. (Whether that change is in position, shape, or property.)
From 4D it is said one could see all six faces of a 3D cube simultaneously.
For us we can achieve the same result by rotating the cube in time.
So you could say time is the 4Th dimension but I don’t know, something seems wrong with that conclusion.
Are the sides in an n- dimensional object are all mutually perpendicular?
Is it possible to have more than 3 sides which are mutually perpendicular ??
Pingback: Q: Can planes (sheets) be tied in knots in higher dimensions the way lines (strings) can be tied in knots in 3 dimensions? | Ask a Mathematician / Ask a Physicist
The thing is,you’re missing one point. Nothing is changed until the third dimension. Then,the deforming starts. You can see that when we see a cube from any perspective except straight ahead(when it looks like a square),all the squares are ‘squashed’. So when you’re visualizing a tesseract(4d hyper-cube),it should have 3 ‘squashed’ cubes as well,disproving the ‘two cubes’ visualization.All dimensions of cubes(starting with a line)should look like the past dimension of cubes. For example,squares look like lines in four different perspectives,cubes look like squares in 6 different perspectives,so we can assume that tesseracts look like cubes in 8 different perspectives. Remember the other visualization of a tesseract(4d hyper-cube)?(the one that looks like a cube inside a cube?). That would be disproved by this. The moral? We can’t visualize a tesseract because it does not exist here and we aren’t used to it. Someone in a 2d universe(if it doe exist) would not be able to visualize a cube(just like we can’t visualize a tesseract) and someone in a 4d world would be easily visualizing tesseracts. Our brains are cut out for this dimension and this dimension only. When you think of squares,you think of a frame,but frames have thickness. We can’t visualize a square with a ‘frame’ that has no thickness. We also can’t visualize a line with no thickness. We visualize lower dimensions in 3d as well. Us ‘visualizing’ 4d is not possible. And don’t get started with the whole ‘time is the fourth dimension’ crap because it’s just us dumbasses calling two totally different things by the same name. We can’t visualize 4d,we can only show it in mathematics. If anything is wrong with this theory,please highlight it for me.(and yes,i am actually eleven)
I really appreciate the comment by the 11 year old. To perceive n-dimensional objects as the dimensions increase, you must be able to simultaneously perceive instances of n-1 dimension. So to see a two dimensional square, you must simultaneously be able to see the four one dimensional lines. If one is only limited to perceive a single instance of the first dimension, a single line, it would be impossible to fathom, or picture/visualize/imagine, a square. If one’s capacity increases to visualize instances of the first dimension, a realm of possible shapes to be imagined opens up, such as squares, triangles, rhombuses, etc. Now if one were able to simultaneously visualize instances of the second dimension, one could perceive three dimensions. Us humans seem to have a limited ability for simultaneous perception of two dimensional images, which is clear from our anatomy. We can only see one two dimensional frame, and use perceptions of lighting/shade combined with logic to construct the three dimensions. If we cannot even fully perceive all two dimensional instances of a cube simultaneously, then how could we possibly perceive multiple instances of three dimensional shapes, granting the ability to visual/imagine in four dimensions.
This goes out to the war veteran. First , thank you. And to the 11 year old genius, thanks for already having stuff to givn when your age is usually concerned with getting stuff.
Seems like war stress makes you feel you have to do the impossible… I have felt it in some 3rd world situations were our free dogs we trained and tagged are killed by anti-terror task force who shouldn’t be used for that..on our beach which is now less secure. I feel I have to save them all. Or at least my two buddies, that live in my room with their fleas ( who are very clever with just a few neurons, but not too clever to do their own heads in by over thinking like we humans) So i suggest to think about 3d +1 space -time. Its more relevant. Say , to understand why three is gravity. Its tricky as well.
But after months i learned to think we are racing through time at nearly the speed of light, which can convert timelike dimensions to space . Dist = light speed * time. can slow near large masses that dilate time. They dilate space also when they are as massive as a star or black hole. So.. the slightest difference in the dilation of time, would make us look towards the planet and see the closer masses paths curve, towards the planet we are racing with, to either bend, orbit, or land there, while we zip on by safely distant or faster.
To visualize 3d space +time ( often called 4d because a higher being might see only different symmetries, to we would be frozen , past /present/ future, ) for that you need to see inside.. an MRI that is moving. you have x,y, z, and T. the scan even says 4d.. “twins fighting ” on youtube shows it. You have 4d of data you could have software to view it/ slice it / and do whatever to make sense of it. 3d +1 , and Riemann surfaces in 2d, are the beginnings of general relativity, if you get any of it you are in Einsteins problem area. The latest idea is that we are actually 2d ( holographic theory) believing we see 3d, because, the information can fit in 2d , and edges can be so complex, and quantum gravity can be solved using the same equations for the big and the small.. Its kind of a cop out but 2d math has become more useful for some than 3d or more for some modelling. We want to simplify the model and find symmetry.
For deeper understanding, think of 2d creatures that can’t imaging the cube. An expanding bubble can have a locally flat area that can hold a galaxy in 2d. So thats an expanding universe. The wormhole? just like an apple. You can visualize it. in 4d space? the wormhole has a sphere to enter.. ( see Interstellar for that). cross the shere borner you are in. is that a tube or hole like we can picture? No.. but its a shortcut in the same way as the 3d universe case with a 2d surface. The 4d universe has a 3d surface. ??? wha.. If we get to there, we rely on the computer. We can use that to understand. The 2d creatures, they draw in like morse code. Well binary is like that.. , we have more space but we prefer to use a 1- D system 1 degree of freedom ( binary 1, or o) for the internet. Just like 2d man probably would .. Books , are possible. Everything except wheels. We don’t understand gravity but an N dimensional theory says orbits of planets are not stable in 4d so life might only be possible in 2d and 3d , +1 . I make a game canned Kontrol that has 2d creatures, 2d physics, and some kids get it and some don’t…But we can capable to understand… Playing the simulation has taught me stuff in the book is wrong and the book taught me my simulation was incomplete with gasses. A brief history of time by Steven Hawking , in the Arrow of time, explains a lot by using a 2d creature who walks on a disk. In my game, based on the Planiverse, not the Flatland, which makes less sense but is far more famous, the creature has a sword that can poke, but cannot slash , because there is no thickness. A sword can block a bullet too. Because there is no going around. you jump over someone coming in your direction.. the creature would see two sets of line segments, in stereo , and perceive depth like we do. From the orthogonal direction that could be time , you can see inside the creatures. A 4d being can see inside us but they don’t exist unless they could emerge without planets, directly from stardust. The 2d world would have disk planets, creatures walking around, gravity towards the center, and not be a floorplan ( there is no room for a floor that way )
People think of 2d as sideview 3d , Mario brothers, but if you read the Planiverse, it is logically consistent. You cant walk left and flip and walk right. You have to back up like a ninja, and turn your tear over to look that way. When he flies a plane, a flying wing, and turns around, he is upside down. you might have to play it to get it.. My game is free, but some levels aren’t but you can email and i give tokens free to people interested because there are not enough people interested yet. 4d games i tried is not fun, you get lost just flying a ship cluelessly. 2d you are a God, helping a little creature.. you can see under the ground stuff he hides by putting any stick to cover it. Ok hope this was useful I am too tired to be concise.
If an 2d object with eyes (with depth perception ability) suppose(closer things appear a darker shade than farther away objects) since then it would percieve every thing in 1d
were to see a sphere
what it would see will be in a 2d world is a darkening of shade from the spheres surface till its diameter and then lightening of the shade back to its surface in 1d
WHEN THE SPHERE PASSES VERTICALLY DOWN INTO THE
plane of the 2d objects existance
Now similar to the 2d object
we 3d objects with 2d perception of depth (think about it)
if were to cross paths with a 4d object wouldnt we see a sphere (we can percieve spheres)
that would go from a point expand uniformly and then contract back to a point
a periodic process which involves time
at different instants if we freeze time we will ” see” different sizes of the sphere
This visualization of and 4d object is in accordance with axes
x , y, z and time (T)
as we can only percieve in 3d or 2d
I can only define 3 spacial dimensions, but I believe we live in four-dimensional universe (the 4th dimension being time) made up of space-time. As a 3D being, we do not see in all 3 dimensions, because we can not see everything around us at once with one eye. As 3D beings, we can move in 3 dimensions, yet not the fourth one. A four dimensional being should be able to move in four dimensions and therefore time travel, while seeing in 3 dimensions. If four dimensional beings were to exist, we would live in a five dimensional universe. This is evident in other dimensions – a 1 dimensional shape (most likely a non-visible line as we see in 2 dimensions) must be part of a 2 dimensional shape, which must be part of a three dimensional shape and so on.
Pingback: Make it: a Tesseract from "A Wrinkle in Time" - Grounded Parents
TO ME IT SEEMS LIKE A LINE SEGMENT CAN BE PASSED THROUGH PERPENDICULARLY TWICE AND MORE THAN THREE SPACE DIMENSIONS WOULD IMPLY MORE THAN 90 DEGREES IN A CIRCLE.A PLANE SEEMS TO HAVE ONE FLAT DIMENSION AND TO ASSUME THAT ALL N-SPACES HAVE INFINITE MORE FLAT DIMENSIONS IS STARTING TO SEEM PREPOSTERIS
In a drawing of a hypercube, one common way is the “exploding” cube schematic. It is easy to see the 8 cubic “faces” by knowing that the inner and outer cube are two, and the 6 truncated pyramid shapes between the two would be perfect cubes in the 4th dimension and all the same size. To build a 3D image of a hypercube we have to distort its parts (cubic faces) because if we fold them correctly they would disappear and we would be left with one regular cube representing one cubic face of the hypercube.