Physicist: Any interaction of any kind that conveys information is a form of detection.
This question crops up frequently in conjunction with the “Copenhagen interpretation”.
The Copenhagen interpretation of quantum mechanics (which comes in a couple different flavors) is generally stated as “a thing is in a super-position of states until it’s measured”. Some people (including very few physicists) have come to the conclusion that “measurement” means “measured by something conscious, and also we’re all part of the same energy field, so we’re psychic, and modern science is only now coming to understand what eastern philosophers have known for millennia”.
Just to be clear, the Copenhagen interpretation is a bottomless font of problems and paradoxes, of which the “measurement problem” is one of the more interesting (but still: one of many). Luckily, since Copenhagen is based on an assumption (“things are in many states until measured”) that never needed to be made, isn’t well-defined, and is in no way supported by any kind of evidence, it can be abandoned giving rise to the Many Worlds Interpretation. Sorrowfully, it’s often found unabandoned (particularly in new age literature).
More often (in sciency circles), Copenhagen is described in terms of a small system (a few particles) in many states interacting with a larger system that’s in only one state, as “big systems” like people appear to be. Somehow that interaction “collapses the wave function”, and only one of the many states of the small system persists.
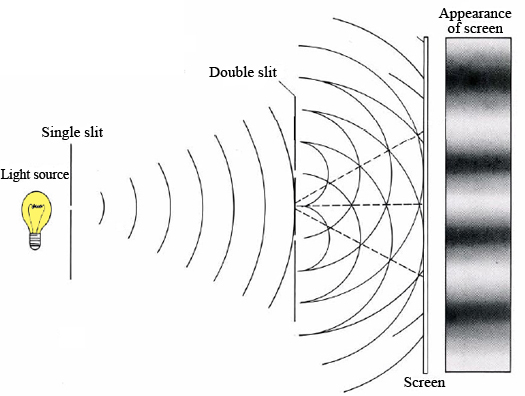
But you may have noticed that experiments like the quantum mechanic’s mainstay, the double slit experiment, can be done in air. That is, you don’t have to remove the air (a very large system) from around the double slits before you do the experiment. The photons (one photon = small system) involved are definitely interacting with air molecules, and yet they clearly continue to demonstrate super-position (being in multiple states). You can even do the double slit experiment off of a mirror, which is definitely a big system. So it’s not just an interaction between a small, many-states, system and a large system that defines a “measurement”, it’s a bit more subtle.
A measurement is best defined as anything that gives you information. And information is what allows you to narrow your choices, or at least refine your probabilities.
For example, when light passes through sugar-water its polarization rotates (you can try it if you like, but for this post don’t be concerned about why it works). But if you don’t know anything about what the polarization of the light was before it entered the sugar-water, you won’t know anything about the polarization afterward. It’s an interaction, but not a measurement. It’s like asking “if I take a coin and turn it over, will it be heads or tails?”. Without knowing what it was beforehand, there’s no new information about what it will be afterwards. In the sugar-water case, this manifests as a conservation of states: if the photon enters the sugar-water in multiple states, it leaves in multiple states (just not the same states).
A polarizer on the other hand definitely performs a measurement. If light goes through, then it’s polarized in the same direction as the polarizer, and if it doesn’t, then it’s not.
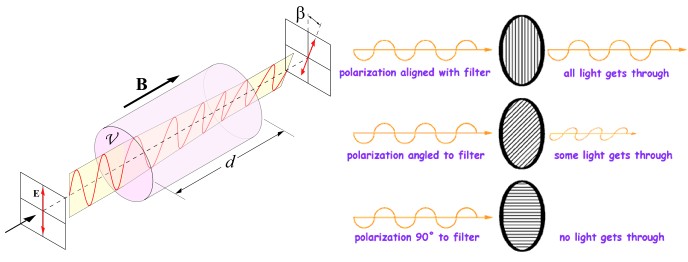
Left: the "Faraday effect" occurs when light passes through a "twisty" material, like sugar. The polarization gets rotated, but not measured. If a photon enters in many states, it remains in many states. Right: A polarizer filters light of a certain polarization. If the photon is in multiple polarization states then the polarizer forces the photon to (from our perspective) "choose" between states. Either it's polarized correctly and passes through, or it's polarized incorrectly and is stopped.
But describing a measurement in terms of information leads to another, possibly nightmarish, question: Is it possible to do a “partial measurement”, that gets only a little information?
If you’ve ever listened to a bus or train announcement you know that it’s possible to get more than none, but far less than all, of the information you’d like. For example; after an announcement you may decide that there’s a 70% chance the train is late, a 25% chance it’s on time, and a 5% chance that someone with a crippling speech defect has violently taken over the PA system. This is a partial measurement, because a full measurement would take the form of 100% probabilities. As in; “the train is definitely, 100%, late”.
Happily, the same is true in quantum mechanics, and it’s extremely useful! For example you can use partial measurements to make “(usually) interaction free measurements”, which is sometimes called “seeing in the dark“. So, you can refine the states of a system without destroying its super-position-ness.
In the double slit experiment you usually set up the apparatus so that there’s a 50% chance of each photon going through either slit (the video in that link is the best explanation I’ve seen, but it jumps the rails a bit around minute 4). “50/50” is just another way of saying “there’s no information about which slit the photon’s going through”.
But there are many ways to gain some information about which slit the photon goes through. For example, you can move the light source closer to one slit, or put some darkened glass over a slit to absorb some photons. Either way, once a photon has passed through the slits you have some idea of which one it went through, but not certainty. As in: “it probably went through the slit that isn’t covered by the darkened glass, but maybe not”.
Any way that you do it, a partial measurement affects the interference pattern. What’s very exciting is that you can slide cleanly from “no measurement” (50%/50%) to “total measurement” (0%/100%).
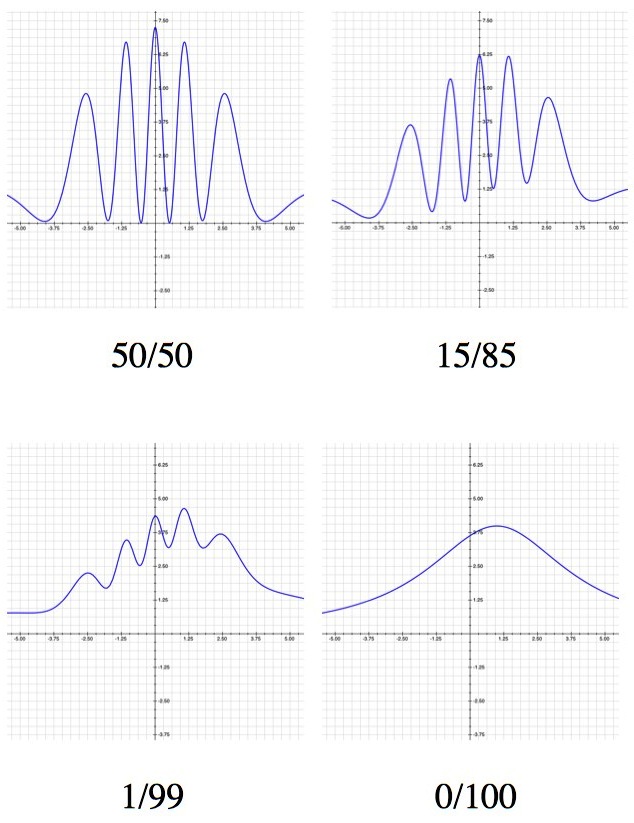
The more you know which slit the photon passes through, the weaker the interference pattern. By the time you're 100% certain which slit the photon goes through (by covering the other or something) you're left with a bump under the one active slit, which is exactly the not-quantum-weirdness result you'd expect.
So, while it’s a huge pain to define “measurement” in a physical context, you can define it pretty readily in a mathematical/information-theory way as “an interaction that conveys information, allowing you to be more certain about what the states are”.
Just to be clear, there doesn’t need to be a person doing a measurement. “Measurement” and “quantum mechanics” may remind you of scientists in labs, but any interaction that conveys information (which in day to day life is basically all of them) is a measurement. If a tree falls in the forest, and no one’s there to see it, the tree and ground still measure each other.







Pingback: Eighth Linkfest
Pingback: Q: What does a measurement in quantum mechanics do? | Ask a Mathematician / Ask a Physicist
Hi Physicist,
You wrote:
“Any way that you do it, a partial measurement affects the interference pattern. What’s very exciting is that you can slide cleanly from “no measurement” (50%/50%) to “total measurement” (0%/100%).”
Can you please provide to references to physical experiments this kind of partial measurement?
Thank you.
Sorry about my typos in my previous reply, here is my
question again: Can you please provide some references to physical experiments of this kind of partial measurement?
I think a measurement is when a wave asks itself, “Do I still exist if I am here as apposed to there?”
Pingback: Q: If quantum mechanics says everything is random, then how can it also be the most accurate theory ever? | Ask a Mathematician / Ask a Physicist
Pingback: Q: What does it mean for light to be stopped or stored? | Ask a Mathematician / Ask a Physicist
So what would happen if you did the double-slit experiment with polarized photons, but behind one slit you put some sugar-water? Does that count as a “measurement”, ie. would you not see an interference pattern? Let’s say the screen showed a different color dot for different photon polarizations, you would be able to tell what the resulting polarization is and thus deduce which path the photon took. If that’s not the case, then how does the photon know that when it’s passing through the sugar-water it needs to collapse its wave-function or not?
@brandon
That would definitely count! When that exact experiment is done (where the photons through each slit have different polarizations) the interference patterns dissappear.
Very cogent explanation, except that I feel I’m stuck only one step further along the road to understanding. I’m left with the impression still that measurement interactions require a person to receive the information–I know that information theory clears this up, but don’t have the mathematical background to follow Shannon’s paper. Is there any example that could give a more intuitive grasp of how we might clearly define an information-conveying (or information-exchanging ) interaction without dragging a conscious observer into it? Are there any good examples of a wave-function collapse that would be expected to occur in the natural world, i.e. apart from the omnipresent physicist with a double-slit demonstration that seems to be the only illustration people use to answer questions of this nature?
“any interaction that conveys information (which in day to day life is basically all of them) is a measurement”
Conveys information to whom?
Doesn’t there still need to be a conscious observer of the information?
A mind-blowing post–I hadn’t seen the data about partial information before.
How does the universe know that darkened glass provides partial information but sugar-water doesn’t?
Pingback: Quantum Break-up | A complete Story of Physics
I want to know in simple terms ( as a layman) what or who exactly is this “Observer”Chap???? that new age Gurus are telling us about ….Does watching or being conscious of an event change the out come??…Is there any Sanity i what i read about the law of attraction etc…Thoughts, waves , and good intentions etc??
Hi
Can someone confirm the following:
1. If the slit experiment was done with the measuring device sending the electron/photon path result to a screen in say the form of a ‘1’ if its true and a ‘0’ if its false for a certain slit AND you do not send a conscious being to view the screen the the electron/photon will act like a wave.
2. if you send an observer to view the screen then the proton/electron will act like a particle.
3. And what I really want to know: if you send an observer to view the screen AND they have no knowledge of the significance of what they are viewing(and in my layman mind are therefore measuring nothing) then what will happen?
Reply to, “Who is the information conveyed to?”: Here “information” means a change in the physical universe rather than knowledge that a conscious person can learn. For example, if a billiard ball rolls across a pool table, it creates a large number of changes–air molecules are shoved out of the way, dust particles and the green cloth are flattened, etc.
The ball creates information as it rolls. A mathematician could track the ball and write mathematical descriptions of all the interactions that the rolling ball creates–he would be noting down the changes in information. The ball also creates changes in energy and matter. These embody the information; energy and matter make the information incarnate; energy and matter materialize the information, so to speak.
When quantum particles are in a superposition, they don’t create information–they don’t create changes in other bits of energy and/or matter. Only upon measurement do they create information. When they have created an actual change in the physical universe, they are being “measured” by other particles in the physical universe, and they are, therefore, creating information. Max Tegmark’s book “Our Mathematical Universe” provides more info on this.
My question is about the question of what exactly constitutes a measurement.
Since a conscious observer is not required, it seems to me that the super-positioned quantum entity interacting with the apparatus that dispenses or doesn’t dispense the poison already constitutes a measurement, so that the cat is already EITHER alive or dead, but not both, BEFORE the physicist opens the box.
In Many Worlds terms, the split of the universes occurs before the physicist opens the box.
What’s wrong with my logic?
And a completely separate concern – in the interest of avoiding unnecessary cruelty, couldn’t Schrodinger have had the apparatus dispense a sleeping potion instead of a poison, so the cat could be awake and asleep (although perhaps not deeply)?
I don’t seem to have made it clear that my question is about Schrodinger’s Cat.
Hi mike death is so much more different from life than sleep is from wakefulness. shroedinger’s point was to show the absurdity of the idea of entanglement and it’s Copenhagen interpretation in although – not a real – experiment
I meant the idea of superposition of states in a thought – not a real – experiment.
Thanks for your clear explanation. The Transactional Interpretation of quantum mechanics, like Many Worlds, solves the Measurement Problem. I find it much simpler than Many Worlds. (Ruth Kastner, “Understanding Our Unseen Reality” for laypeople. In 2012, she also published a technical presentation of John Cramer’s Transactional Interpretation with her additional developments.)
“A measurement is best defined as anything that gives you information. And information is what allows you to narrow your choices, or at least refine your probabilities.” I came all the way to the end to say this process gives the system being measured information about us, too, but the last paragraph beat me to it, and in agreement with Alexandra Hopkins on Kastner and TI, and many of the other excellent discretized space theories, from Loop Quantum to Causal Set, and Kastner’s TI works with Causal Set, and in such, such, SUCH agreement that emergent space makes so much more sense than MWI. It is more conservative, more consistent, more reasonable.
The craziness new age people have come up with to account for quantum theory has NOTHING on the craziness physicists have come up with to shoehorn it into continuous spacetime.
And if you want to bring up gravity and clocks, read EINSTEIN’S UNFINISHED REVOLUTION for a background-independent version, or watch any of Fay Dowker’s many public lectures for a relativistic version. There are excellent alternatives to MWI that answer Weinberg’s question: how do probabilities get into the deterministic Schrodinger equation? Agree with Alexandra Hopkins (above) on Kastner’s popular book. It’s excellent, even if you don’t agree with TI. As I said, it is consistent with Causal Set, and you can find her paper on that work online. String Theory and MWI are not the only alternatives to Bohrian mysticism, but, honestly, once you start digging, you’re going to find a way nature is that is strange and beautiful that really has nothing to do with quantum mechanics, but with rest 🙂 I think everybody has a piece of what’s going on, and science has the hard job of having a sufficiently complete picture to choose and control outcomes of a future many scientists don’t even believe is possible for them to change :)))))
Hi Penny. You said, “A measurement is best defined as anything that gives you information” I can’t understand this at all. Who is the “you” , You mean yourself or any person ? When I think about this stuff , it always come to me and me alone as the only thing in the universe that observes. When I observe something , I immediately collapse all the wavefunctions all the way back to the big bang and in the process create all the other people also. No one can observe me as in Wigners friend. https://en.wikipedia.org/wiki/Wigner%27s_friend
Quantum mechanics starts off with a measurement. There is no collapse. Every experiment needs a priori a result , then you do the math and the math is a wave form.
So in the Schrodinger’s cat experiment, the measurement is made, ie the box is opened. That is the experiment. If you are a second scientist standing outside the room where the first scientist opens the box. Well that is a different experiment and you can’t combine the two waveforms , one in the box with cat and the other in the room with scientist. You have to start from zero and make one waveform for the whole room with the box inside it. The guy standing outside then opens the door to the room and make a measurement by opening the door.
So actually there were other waveforms before the box part also. Who set up the experiment with the box and other complicated things. Inevitably you have to go all the way back to the big bang.
The many worlds interpretation fails also because what makes you take one route through history over any other route. You still need something to decide your direction, something like a measurement. The many worlds interpretation does not have measurements but that is the first thing mentioned in the quantum theory, “the measurement” . So you have to have a measurement and it has to be done.
When you have the cat in the box in a half dead, half alive state, that is very good but it assumes you are going to open the box. It assumes you are going to make a measurement by opening the box. If you stand outside the room and let someone else open the box, then the whole experiment changes.
Could the following be a suitable definition of “information” as the term is being used here? …
“‘Information’ about an entity consists of any changes in the states of any othet entity as a result of an interaction with the original entity.”
Typo correction: other*