Mathematician: If you have a function f(x) and a function k(x,s) then you can (as long as the product of f(x) times k(x,s) is integrable on the set X) always form another function of a new variable s as follows:
We have just “transformed” the function f(x) into the function F(s) via an “integral transform.” Why the hell would anyone want to do this? Well, the function F(s) is sometimes easier to work with than f(x) itself, or tells us interesting information about f(x) that it would be hard to figure out in other ways.
Of course, the interpretation of this new function F(s) will depend on what the function k(x,s) is. Choosing k(x,s) = 0, for example, will mean that F(s) will always be zero. This is pretty boring and tells us nothing about f(x). Whereas choosing will give us the sth moment of f(x) whenever f(x) is a probability density function. For s=1 this is just the mean of the distribution f(x). Moments can be really handy.
A particularly interesting class of functions k(x,s) are ones that produce invertible transformations (which implies that the transform destroys no information contained in the original function). This will occur when there exists a function K(x,s) (the inverse of k(x,s)) and a set S such that
that undoes the original transformation (or, at least, undoes it for some large class of functions f(x)).
Whenever this is the case, we can view our operation as changing the domain from x space to s space. Each function f of x becomes a function F of s that we can convert back to f later if we so choose to. Hence, we’re getting a new way of looking at our original function!
It turns out that the Fourier transform, which is one of the most useful and magical of all integral transforms, is invertible for a large class of functions. We can construct this transformation by setting:
which leads to a very nice interpretation for the variable s. We call F(s) in this case the “Fourier transform of f”, and we call s the “frequency”. Why is s frequency? Well, we have Euler’s famous formula:
so modifying s modifies the oscillatory frequency of cos(xs) and sin(xs) and therefore of k(x,s). There is another reason to call s frequency though. If x is time, then f(x) can be thought of as a waveform in time, and in this case |F(s)| happens to represent the strength of the frequency s in the original signal. You know those bars that bounce up and down on stereo systems? They take the waveforms of your music, which we call f(x), then apply (a discrete version of) the Fourier transform to produce F(s). They then display for you (what amounts to) the strength of these frequencies in the original sound, which is |F(s)|. This is essentially like telling you how strong different notes are in the music sound wave.
Below are a few other neat examples of integral transform.
The Laplace transform:
This is handy for making certain differential equations easy to solve (just apply this transformation to both sides of your equation!)
The Hilbert transform:
This has the property that (under certain conditions) it transforms a harmonic function into its harmonic conjugate, elucidating the relationship between harmonic functions and holomorphic functions, and therefore connecting problems in the plane with problems in complex analysis.
The identity transform:
Here is the dirac delta function. This is the transformation that leaves a function unchanged, and yet it manages to be damn useful.







Perfect, I’ve been taught about Fourier, Laplace transforms and Green’s function, but never had them all tied together – if only someone had explained to me they were all just a specific form of a generalised integral transform!
More Fourier transform magic.
Say we have some partial differential operator with constant coefficients. For concreteness’ sake, let’s let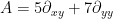 , but this will be true for any such PDO. Then for ANY (reasonable) function f, the Fourier transform
, but this will be true for any such PDO. Then for ANY (reasonable) function f, the Fourier transform  is …
is …  .
.
In other words, partial differentiation gets taken, under a Fourier transform, to multiplication by polynomials. That is, a most mysterious and difficult-to-understand mathematical phenomenon is, from a different perspective, one of the easiest and best-understood!
Words do not fully express how awesome that is.
Pingback: Weekly Picks « Mathblogging.org — the Blog
Pingback: Tenth Linkfest
What are indefinite integrals?
They are the “inverse operation” of derivatives. When taking an indefinite integral of some function F, you ask yourself “the derivative of what, will give me F?”.
plz tell me how the integral transform works on matrices and how the inverse integral transform works on matrices?
Nice article … but for Radon transform, what is its kernel function k(x,s)? Does it fit into this framework?
How can we generate integral transforms to help us solve some integral equations?