Q: What is the three body problem?

Physicist: The three body problem is to exactly solve for the motions of three (or more) bodies interacting through an inverse square force (which includes gravitational and electrical attraction).

The problem with the 3-body problem is that it can’t be done, except in a very small set of frankly goofy scenarios (like identical planets following identical orbits).

The unsolvableness of the 3-body problem, rather than being an embarrassing hole in physics, an obvious but unsolved problem, is actually the norm.  In physics, the number of not-baby-simple, exactly solvable problems can be counted on the fingers of one hand (that’s missing some fingers), and that includes the 2-body problem.

The dynamics of one body is pretty straight forward, in as much as it travels straight forward.

The dynamics of two bodies, while not trivial, can be reduced by pretending that one body is sitting still, and then restricting all of your attention to the other body.  Using that technique, you find (or, at least, Newton found) that the motion of a body under gravity is an ellipse.  The same idea can be applied to the quantum mechanics of electrons and protons to find the exact structure of the electron shells in hydrogen (1 proton + 1 electron = 2 bodies).  In that case you’re not talking about actual orbits, but the idea is similar.

But, for three bodies, there doesn’t seem to be a fancy trick for finding solutions.  As a result, the exact behavior of 3 or more bodies can’t be written down.  The exact energy levels and orbital shell shapes in anything other than hydrogen is impossible to find.  Even deuterium (hydrogen with one extra neutron)!  Can’t be done.

Despite that, we do alright, and happily, reality doesn’t concern itself with doing math, it just kinda “does”.  For example, quantum field theory, despite being the most accurate theory that ever there was, never involves exactly solving anything.  Once a physicist gets a hold of all the appropriate equations and a big computer, they can start approximating things.  With enough computing power and time, these approximations can be made amazingly good.  Computer simulation and approximation is a whole science unto itself.

But even with just mechanical pencil and paper there are cheats.  For example, although there are more than three bodies in the solar system (the Sun, eight planets, dozens of moons, and millions of asteroids and comets), almost everything behaves, roughly, as though it were in a two body system.  Basically, this is due to the pronounced size differences between things.  As far as each planet is concerned, the only important body in the rest of the universe is the Sun.  To get some idea of why; the Sun pulls on the Earth about 200 times harder than the Moon, and about 20,000 times harder than Jupiter.  Nothing else even deserves a mention.  So, if you want to calculate the orbits of all the planets, a “2-body approximation” will get you more than 99% of the way to the right answer.

But that last 1% has a lot of weirdness in it, most of which falls out of chaos theory.  The more interesting part of chaos theory is the “islands of stability”, or what we in the biz call “chaotic attractors”.  While you find that no real life N-body system orbits are stable (exactly repeat themselves), you do find that they settle into patterns.  For example, while the system of Jupiter’s innermost moons: Io, Europa, and Ganymede, never quite repeats the same path, they do manage to “resonate” with each other and settle into a rhythm.  Hence the name; “orbital resonance“.

Basically, when you have several bodies orbiting a much larger body, the length of the orbits of the smaller bodies will tend to settle into simple-fraction (1/2, 2/3, 1/3, etc.) multiples of each other.  1 to 2 to 4 for Io, Europa, and Ganymede.  The slight ellipses of any real-life orbits cause the gravitational force of the moons, to “pulse” (becoming slightly stronger or weaker) along another moon’s orbit.  As a result (this is not at all obvious right off the bat) if the other moon slows down it gets pushed a little faster at regular intervals, and if it gets too fast it gets slowed down at regular intervals.

The moons still have very elliptical orbits (a symptom of being in a 2-body system with Jupiter), but the presence of the other moons does affect how big that ellipse is, and in what direction it “points”.

When you have even more bodies you can almost abandon the idea that there are any bodies at all, and move over to fluid dynamics.  Although, again, that’s just an approximation.

(upper left) The 2-body Earth/Moon system as seen from one of those bodies.  (upper right) The 5-body Jupiter/Galilean-moons system as seen with binoculars.  (bottom) The more-than-a-few-body Andromeda system as seen with some kind of big-ass telescope.

Point is, this effect only shows up in systems with three or more bodies, it’s chaotic (in the chaos theory sense), and there is no way to predict it exactly.  That being said, we can still get computers to come pretty close (up to a point, because chaos is a punk), and there are even some mathematical tricks to get reasonable solutions that, while not perfect, are still pretty good (and can even get us well into that last “1% of weirdness”).

Answer gravy: First, this is how to solve the gravitational two body problem.

Take two masses, and , with positions given by and .  Then the force on (keep in mind that F=MA) is given by Newton’s law of gravitation:

Where “” is the vector that points from to , and the double-dots on the left hand side indicates the second time derivative (which is math speak for acceleration).

If it bothers you that the bottom of the right side is cubed (not squared), it’s because this is a vector equation that includes both the magnitude of the force and the its direction.  If you look at just the magnitude of both sides you get .

Now, since for every action there’s an equal, but opposite reaction (every force is balanced by another force):

Now check this out!

At this point just replace “” with ““, and “” with ““.

Then jump over the the elliptic orbit post to find the ellipticalness of this.  The subtle, unspoken assumption of that post is that the Sun doesn’t move (i.e., it was already stated in the “reduced form”).  Which is exactly what this math has been setting up.  “” is called “the relative position vector”, and all it does is point from the second body to the first body.  So describing its dynamics is the same as describing the dynamics of a world where the second body is stationary.

So here’s the tough part.

In the 2-body problem all you have to worry about is the attraction between body 1 and body 2.  In the 3-body problem there are 3 attraction terms to worry about.  In the 4-body there are 6, in the 5-body there are 10, etc. (in general there are terms for N bodies, which gets bad fast)

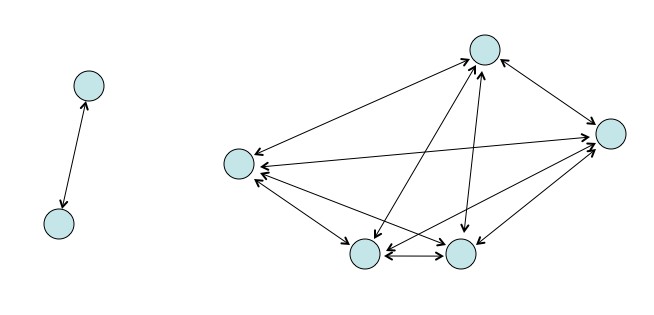
The ease of the one attraction term in the 2-body problem vs. the horror of the 10 attraction terms in the 5-body problem.  Readers are invited to note that 5 isn’t even that big a number.

In the 3-body problem, in order to find the total force on body 1, body 2, and body 3 you have to add the attraction from each of the other bodies:

It could be worse; it could be that somehow the other bodies interact with each other in such a way that the total force is different than just the sum of their independent forces.  In fact, almost any other set up is worse.  Even things like declaring “only the closest body attracts”.  That would be much worse.

So, even if you set up one of the bodies to be stationary (like in the solution to the 2-body problem), you still end up with N-1 bodies flying about, and you still have force terms to worry about (N-1 for N equations, but by Newton’s third law the force of A on B is equal to the force of B on A, so divide by 2).

Exact solutions just don’t seem to exist.