Physicist: The short answer is: A worm hole is a “tube made of spacetime” that connects two different regions. If it’s set up right, you could enter one side of the tube and exit the other end somewhere else, or even somewhen else. In contrast, a black hole destroys the hell out of things, and doesn’t “go anywhere”.
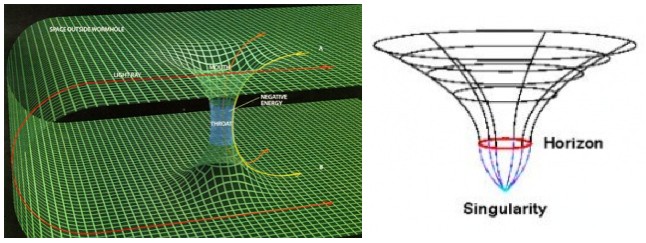
A worm hole is a funnel (what’s shown here is only a two dimensional funnel) that tapers down to a “throat” (which although thinner never pinches off entirely) which connects to another funnel that opens up somewhere else. A black hole is a funnel that pinches off at a singularity. A traversable worm hole needs to be large and “mellow” enough that it doesn’t have an event horizon (a black hole’s “point of no return”), or any fatal tidal forces.
There’s a long history of the two being mixed up. For example, there are a number of stunningly bad movies that make the connection between black holes and worm holes explicit. But even in legitimate (non-Hollywood) physics circles you’ll sometimes find people talking about “going through” black holes, as opposed to (or in addition to) “being destroyed a lot” by black holes.
Over the years physicists have gotten a little gun shy about ignoring solutions. For example, one of the clearly impossible solutions to the Schrodinger equation (which describes the wave nature of things) involves particles crossing through impossible boundaries. Turns out they can, and it’s now called “quantum tunneling“. In fact, you probably even own some electronic devices that take advantage of this “impossible” solution!
Another example is when Dirac took the Schrodinger equation and re-wrote it in a relativistic form to create the Dirac equation (the original equation isn’t compatible with relativity). He found that he suddenly had a second set of solutions which imply the existence of anti-particles. At the time the idea of an anti-particle was ridiculous, but a few years later positrons (anti-electrons) were discovered and Dirac was shown to be right.
So, given the history, physicists today are a little hesitant about chucking out solutions, even when they’re silly. And black holes are a bottomless pit of math with solutions that seem impossible.
The singularity at the center of a black hole is usually described as a point. However, this is a symptom of our paltry computational power back when black holes were first being theoretically researched. A singularity can actually take a number of forms. According to a variety of (modern/powerful) computer models, as a star collapses to form a black hole it often finds itself forming “singularity sheets” in areas where its density becomes large enough. All of it ends up in the same tiny singularity moments later, but it’s still interesting. In a spinning black hole (which is all of them, to some extent or another) the singularity takes the form of a “ring singularity”, which is exactly what it sounds like.
One of the wild things about ring singularities is that they make the topology of spacetime qualitatively different, in a way not entirely dissimilar to the way that the surface of a sphere is qualitatively different from the surface of a doughnut (or, for our New York readers, a bagel).
In normal, everyday space, if you travel in a big loop you come back to the same place. If you were a mathematician you would prove this using a “continuous deformation”.
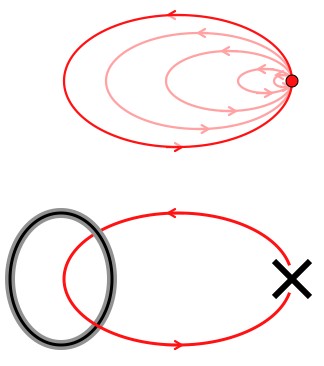
In ordinary space moving in a loop has the same net effect as not moving. But if your loop takes you through a ring singularity, that may not be the case.
A big loop is nearly the same as a slightly smaller loop, is nearly the same as a slightly smaller loop, is nearly the same… is nearly the same as a point. If there’s a singularity in the way the loop that goes around it can’t be smoothly deformed into a loop that doesn’t. As a result, traveling on a path that takes you through a ring singularity doesn’t necessarily need to bring you back to where you expected to be.
As hand wavy and weird as this idea sounds, it has a lot of mathematical relevance. It shows up all the time in complex integrals and branch cuts, and just a hell of a lot in algebraic topology. But, to be fair, nobody’s ever seen a physical “doorway through space and time” kind of example.
Beyond just the singularity, there are a lot of weird problems involving picturing how black holes work. For example, they screw up spacetime so much that at their surface (the “event horizon”) time literally points downward. Not only do you have to contend with the fact that spacetime is four dimensional (3 space directions plus 1 time direction), but the time direction is very different, so it’s four dimensional in a really weird way. Now add to that that black holes royally mess things up and you’ll find yourself in dire need of a better coordinate system to make things easier to picture.
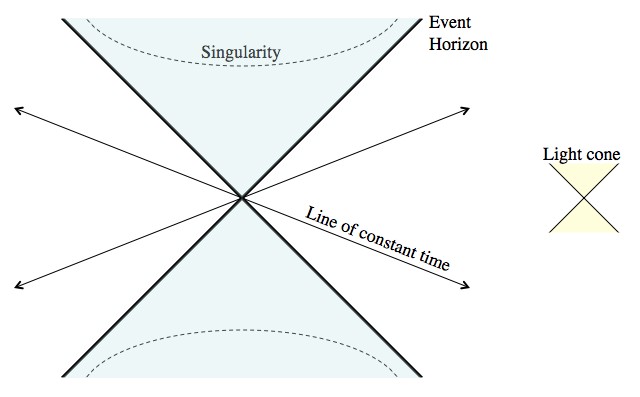
A black hole in K-S coordinates. Light travels at a 45° angle everywhere in this diagram, which physicists like, but everything else is weird.
Enter Kruskal–Szekeres coordinates. Although the situation is still a little weird, time points more or less up (the standard set up for space/time diagrams), and light travels diagonally (again: standard). In these coordinates all of our universe is on the right side, including all of the past and future, the event horizon of the black hole is the upper diagonal (and, oddly enough, the infinite future), and the singularity is a sweeping curve in the top area. Keep in mind that this coordinate system is more than a little bit weird. For example, they assume that the black hole exists forever (into the past and future) at the same size. So the bottom diagonal is an unashamed representation of the infinite past. Any finite time in the past (say, the beginning of the universe) would be slightly above the lower diagonal.
Now the point: you can write down a lot of the physics of general relativity in these coordinates and they look pretty good, so it feels like there’s something to them. However, they include a left side. General relativity treats the stuff on the left the same way it treats everything on the right (our universe). So, if the left is something more than just a mathematical artifact, then it’s another space and time completely independent from our own. Since nothing travels faster than light, which in these coordinates travels along diagonals, it’s impossible to get from any point in our universe to the other universe. However, if you fall into the black hole you can see someone from the other universe that’s also fallen into the balck hole, and have a nice chat before you’re both destroyed at the singularity.
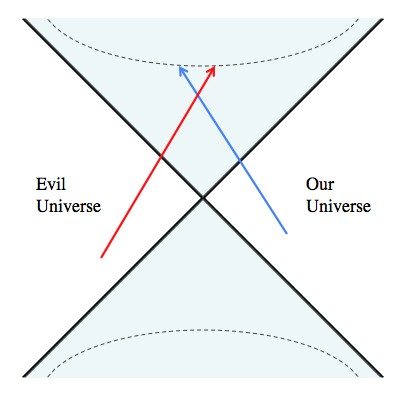
Although you’d need to travel faster than light to get from one universe to the next (if the next exists), you can meet other doomed travelers from the next universe without traveling faster than light. The upside is making new friends. The downside is being destroyed in a black hole.
If faster than light travel were possible, and if there were another spacetime on the other side of the black hole that wasn’t just a mathematical convenience or ring singularities behave exactly like we want them too, and if you could make it into and out of the black hole without being destroyed a lot or taking forever doing it (it takes literally forever to fall past the event horizon), then black holes are certainly doorways to other universes, or different parts of our own.
So, to the point, there’s a history of people confusing or blurring the distinction between black holes and worm holes, and not completely without reason, but in general: black holes mean stop and worm holes mean go.







The word “hole” could mean both a “hole in the ground” and a “hole through a wall.” I think people get confused because they think an astronomical “black hole” is the latter use of the term.
Should we call them astronomical “black pits” instead, to prevent confusion ? I think the term “cosmic oubliette” would be more evocative, but we have enough trouble with a simple word like “hole.”
Pingback: Linkblogging For 20/10/11 « Sci-Ence! Justice Leak!
It’s not so much that people get the term wrong, thinking of black holes as holes in walls, as it is that people fail to realise that getting anything through the event horizon of a black hole in any shape remotely resembling something coherant is quite completely impossible. The average layperson just doesn’t recognise the absolute barrier of the event horizon for what it is.
Most of the time whenever crazy physics crops up around black holes the answer seems to be “Yes you can do that, if by yes you mean no because there’s an event horizon in the way.”
Thanks for this informative article. But according to what I’ve read, there actually are circumstances in which it might be possible to traverse a black hole in some sense. These occur when the black hole is sufficiently charged or rotating or both. In these cases the singularity is “vertical” in the Kruskal-Szekeres or Penrose diagrams. That means that a travel need not collide with it. This allows the traveler to emerge from white-hole into other so-called “asymptotically flat regions” that might or might-not be part of our universe. It’s not certain, however, whether the white-hole from which the traveler would emerge is stable, whether the traveler would survive passage through interior horizons on which energy collects, or whether the lack of predictability of the traveler’s path beyond so-called Cauchy horizons (beyond which nothing can be predicted) is meaningful.
Source: The Physics of Stargates — Parallel Universes, Time Travel and the Enigma of Wormhole Physics by Enrico Rodrigo
thank you i needed this realy badly 4 h.w.
Pingback: THE BLACK HOLES THAT ARE MY BLOGS « Behind the Lens
How Black Hole dies?
Hawking radiation, and patience.
As mentioned above, that worm holes are of funnel shaped that open somewhere else,so probably they can also have their event horizon depending upon the depression they make in space-time fabric, particularly not ending at singularity as black holes. So by applying the same Kruskal–Szekeres coordinates how will the worm hole differently lead to somewhere else from evil universe’s white hole (as black hole does)? how the somewhere else place(opening of the white hole) can only be a place in our universe?
He he he.
Does this article imply that black holes and wormholes actually exist? I read that they are only theoretical.
Black holes yes, worm holes no.
To date we’ve confirmed several dozen black holes, but there are strong indications that every good-sized galaxy has a super-massive black hole. The Milk Way’s central, super-massive black hole is Sagittarius A*.
i studied in physics that black holes can deforme space time and create wormholes. is this true in some way??
if i’m not mistaken, it’s stephen hawking that talks about black holes that are worm holes? i’m really confused 😛
DOES THE OTHER ENDS OF BLACKHOLES(WHITEHOLE) EXIST IN OUR UNIVERSE?
Can a warm hole be named as antiblackhole which can exist in pairs and can separted from each others due unknown type of energy
There is only one white hole. All the matter that feeds into all the black holes in all the universe over all of time has the same exit point: The Big Bang. So the universe and time itself are cyclical in this respect.
Source: my imagination 😉
My imagination tells me that black holes are not really holes but objects, like star or planet but so dence that its gravitational pull drags and squashes everything to the point where it gets transformed, blended into more basic (dark?) matter/energy, perhaps sth of a form of radiation that eventually leads to this black hole’s vaporization. Depending on how big the black hole is, it will last for as long as the staff it was made of continue processing the “incoming” matter. Once it runs out of its fuel it disappears in form of radiation or dark energy/matter or both…?
Pingback: Dilatasi Waktu
What I think is this , black holes arent really “holes” . If you try to get through it you’ll fail because once you’re there you will turn into millions of pieces and all of your atoms will separate and you yourself will become part of the black hole. However the wormhole is diffrent , we could say it has 2 mouths on each side that are connected with a tube , if you go through it you could eaither go to a diffrent Galaxy, go to the future or if not to the past. For example if you have 2 clocks and you go through the worm hole one clock will say your time lets say 2005 however the other clock will say 2000 you’re basically 5 years into the past. Also going through the worm hole would take thousands of years even if you’re going through the speed of light, however for you it’ll only be a short amount of time and you would age much slower so once u return back to earth it’ll be about a thousand years later and you wouldn’t look much different. It’s certainly possible you could go through a worm hole but the problem is that you never know when the worm hole would shut closed and If you’re inside the wormhole while that happens you will die but if you have crossed the worm hole and it shuts closed you’ll be stuck in a whole other Galaxy or dimension. Well yeah that’s what I think .
I’m not sure the concept will ever be anything more than fantasy.
Ultimately, a wormhole is an attempt to travel through 4-dimensional space. In such a situation, it would be more appropriate to map the spacetime geometry as a sphere, rather than a flat surface folded over, and inside the sphere is 4-dimensional space.
As a sphere, every trough in the geometry that marks gravity moves towards the centre point. So in order to get to another point within the 3d universe you’d need to move to the centre point and then move from there down another “tube” to your destination. The problem is that centre point is where mass is infinite (ie. a singularity). In other words, it’s a black hole.
please do more research with black holes
I’m confused….black hole creat….and do go places..move..bend…and fluctuate. ….and how do you know that worm holes have own event horizon..also..why do you write that singularity will destroy? Have you witnessed this? From what I know singularity creates life..just not what we think of as life…look at the beauty of it…ergo…our universe was a singularity and we are here and everything else..thank..please reply
Pingback: Wormholes | Science of racionality
all you guys are smart 🙂 thank you for the information everything is so interesting wow :0 perfect
John paul you are talking about initial singularity
So pretty much, the event horizon is the “point of no return” in a black hole, making travel impossible due to the amount of destruction of matter on a molecular scale?
it is really a good information but i want to know that the black hole contribute its share(in the even horizon) in the universe and by how it moves from one planet to another?
wow….so informative…thanks….though didnt clearify the thought….
Does it mean when a super massive blackhole gets absorbed by another super massive blackhole !!!!is that space is called God’s space??
After life, do we travel to that super massive blackhole space and go thru that funnel and take new life in other super massive blackhole space…. Is that is what the LIFE CYCLE is all about? …or is our LIFE and the LIFE OF UNIVERSE is neglegent in this massive substances….
#ThinkerBellQuestion : What is their when a Super Massive Blackhole gets absorbed by another Super Massive Blackhole ?
The difference between blackhole and wormhole :
blackhole is a big thing that can take anymore and we cannot assume that were we go
In case of wormhole is invisible thing it is so hard to be stabled It can take so long years to stable but it can take where ever you think
Actually, to keep a wormhole from collapsing you’re going to need a hell of a lot of negative matter. Also, I doubt that wormholes are invisible. If you somehow got enough negative matter, yes it would be hard to stabilize it, but no it would not take years. It’s mainly hard to stabilize because negative matter/energy has never been isolated.
Great information there. But I have a few questions. Why do we anyway believe in existence of wormholes if they have never been seen or discovered? Black holes exist though. And how long is a black hole’s life cycle? Why does a big dead star/sun forms a black hole? Where do all the sucked-in debris go after crossing over the “event horizon” if at last they finally reach the singularity OR nothing ever reaches the singularity due to the fact that falling speed reduces to nearly zero?? OR the debris keep revolving (but utterly slowly) till infinite time like earth revolves around the sun? Gosh I have too many questions !
So, if I understand the material correctly, it’s the event horizon that destroys everything that enters the black hole, not the singularity? Just confirming that I understand the material so that I don’t accidentally spread false information on the topic.
@Brett Peardon
I should make that more clear in the article.
An event horizon doesn’t destroy things on its own, but it may as well. Outside observers see things approach, but never quite reach the horizon, as their clock slows to a stop. For observers falling through, the event horizon is a point of no return, and a worm hole you can’t exit isn’t super useful.