Entanglement omnibus!

We’ve recently gotten several short questions about entanglement.  In keeping with other, better, “ask” services: entanglement omnibus!

Q: What is entanglement? (nobody asked this, but it’s a good place to start)

A: If you understand what correlation is, then you’re 90% of the way to understanding what entanglement is.  Say Alice and Bob each have a marble in a box.  For reasons beyond contemplation, Alice and Bob have always been perfectly happy with one Blue marble and one Red marble.  Neither of them knows which marble they have, but they both know that they have different colored marbles.  The moment either of them looks at their marble, no matter how far apart they are, they’ll suddenly know what color the other marble is (correlation!).

For each of them the marble they have is completely random.  The only time they notice anything interesting is if/when they meet up to compare results, and find that their results are always opposites.  This “opposite color marble” thing is just one form that correlation (entanglement) can take.  You could also set up a “same color marble” thing.

Entanglement is nearly the same as simple correlation.  The difference is that while regular correlation involves states that are merely unknown (the marbles are each a particular color, it’s just that nobody knows which is which), entanglement involves particles in multiple states.  “Quantum marbles” can be both red and blue, at the same time (when things are in more than one state at a time they’re said to be in a “superposition“), and yet be correlated with each other. That shouldn’t make much sense, so don’t stress.

There’s an older post that may help you build intuition a little.  In very much the same way that a single particle can be in multiple states (like a single particle going through both slits in the double slit experiment), two entangled particles are in two states together.  In the marble example the two quantum marbles are in a superposition of the two states “marble 1 blue, marble 2 red” and “marble 1 red, marble 2 blue”.

Because notation will be useful in a minute, here’s how you would notate a couple situations:

Also, there are several ways to write states, depending on what you’re trying to say.  For example, .  The first form is a little cleaner/standard, but the last form makes it clear that the first marble is always red, while the second marble is in a superposition of red and blue.

Q: How are entangled particles created?

A: There are a lot of ways that particles can be entangled.  Almost any piece of information you can have about a particle is something you can entangle.  For example, the directions a pair of particles are moving in.

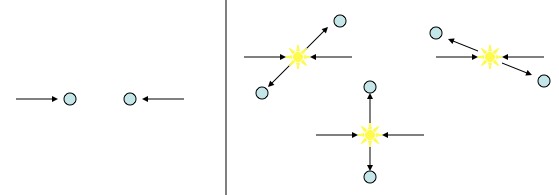
When things bounce off of each other, they bounce in opposite directions.  While particles can be in many places, and move in many directions at the same time, in this case they need to do it in opposite directions.

If you bounce a couple of particles off of each other, you won’t be able to say which direction either one bounces in, but you will be able to say that they’re bouncing in opposite directions.  Generally speaking, when a quantum physicist says “you can’t know which of these things the particle did” what they really mean is “the particle did each of those things at the same time”.  The particles are bouncing apart in a superposition of directions, but in a correlated way.  Entanglement!

If you have a method of generating particles in pairs, but at random times, then the particles so created will be entangled in terms of their creation times.  That is: you have two particles flying around, you don’t know when they were created, but you don know that they were created at the same time.  Their ages are entangled!

Another classic example; if you create an electron/positron pair (“positron” = “anti-electron”) they must have opposite spins.  This is guaranteed by the conservation of angular momentum; if nothing is rotating then the angular momentum is zero and if the particles are spinning in opposite directions then the angular momentum stays zero.

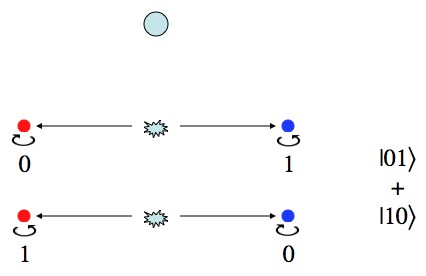
When an electron/positron pair is created they’re always spinning in opposite directions.  So, even though they each spin in a “superposition” of directions simultaneously, they do it in such a way that they’re always opposites.

So, you can have clockwise/counterclockwise, counterclockwise/clockwise, or (since you can have things in multiple states) a combination of both.  Or, saying the exact same thing using the notation in the picture above: , , or .  Notice that the states and never show up, because they would involve the particles spinning in the same direction.

Notice, by the way, that it isn’t enough to talk about the states of each particle one at a time.  In order to describe things accurately requires us to talk about the “state of the system”.  In both of the examples above (and in any example involving entanglement) the particles involved are in multiple states, but knowing the states of each particle individually doesn’t tell the whole story.  Entangled particles share states with each other.  In the last example, there’s no way to express in terms of just one particle and then the other.

In practice, photons are the easiest particles to work with.  They’ve got nice, big, easy-to-work-with wavelengths, they’re incredibly easy to create (in fact, try not to make photons), and they’re easy to entangle.

The most common method (used in fancy labs and whatnot) is to use a “parametric down conversion crystal“.  You fire a photon at the crystal, and for reasons best described as “stupid-complicated”, two photons of half the original frequency are spit out the other side.  These new photons are entangled such that their polarizations are the same (type 1 crystal) or opposite (type 2 crystal).

A little more abstract, if you can get a “quantum controlled not gate”, then you can induce an entanglement.  There are slightly more ways to create a controlled not gate than there are ways to create a quantum computer (many), but the idea is always the same.  A controlled not gate involves two bits: a Control bit and a Target bit.  If the control bit is 1, then the target bit is flipped, and if the control bit is 0, then the target bit is left alone, and if the control bit is in a superposition, then the target bit will likewise be in a superposition of flipped and not flipped.

Starting with a control bit in the state (technically, a superposition of zero and one is called a “qbit“) and a target bit that’s in the state , you have the overall state: .  The effect of the c-not gate is:

which is entangled!  Before the c-not gate is applied the state of one bit tells you nothing about the state of the other, but afterward the state of each tells you everything about the other.  Those mothers are hella entangled.

Q: Can more than two particles be entangled?

A: Hells yes!  So far, the record for the largest number of “maximally entangled” particles is 14 (“Maximally entangled” means “perfect correlation”).  Entanglement can take a lot of forms, but one example state of perfect 14 particle entanglement would be something like: .

Q: Could a home scientist hope to create entangled particles?

A: It depends…  I don’t think a home scientist could keep track of a single particle, let alone an entangled pair.  That being said, most interactions create entanglements, but not interesting/useful ones.  When air molecules bounce off of each other their motion becomes entangled, but really; who cares?  There’s a lot of air, and a lot of molecules bouncing off of each other and getting entangled, but none of it is useful or controlled.

So, you are entangling yourself with everything around you all the time, but that’s clearly not the spirit of the question.  The spirit of this question is (probably) about perfectly entangled, two-state systems.

If you really wanted to, you could buy a down conversion crystal, some lasers, some photo-detectors, and all the rest of the equipment necessary to do entanglement experiments.  It’s expensive.  However, there are some examples of “clean” entanglement (not just stuff randomly interacting) that you can find around the house.  Specifically: carbon rings.

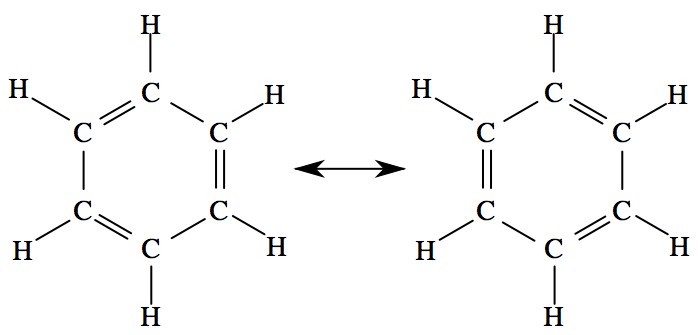
Benzine (shown) is the simplest carbon ring.  Carbon rings  have two ways for bonds to arrange themselves, and in fact exist in a superposition of those two states.  The bonds are each entangled with each other: if you know whether one is a double or single bond, you know what each of the others are.

Carbon likes to have 4 bonds.  It also likes to form rings that are six atoms around, and even chains of those rings.  Many organic molecules are put together with pieces like this.  But when so arranged, each carbon is only bonded to three other atoms.  It gets a fourth bond by doubling one of those bonds.  But (check the picture above), this establishes an arrangement of double and single bonds all the way around the ring, so the single/doubleness of each bond is correlated to each of the others.  And, rather than being in just one arrangement or the other, carbon rings exist in a superposition of both.  Superposition of states with correlation?  Entanglement!  It’s not terribly exciting, but many of the atoms and bonds in your body are involved in some very clean, two-state entanglements.

So, technically you create maximally entangled particles by being alive and eating food, because they’re a part of a lot of the chemicals that we naturally produce.  But, of course there’s no way to verify that entanglement using just the sorts of things you’d find around the house.  So… I suppose you can just take comfort in the knowledge?

By the way, if you know a biochemist, ask them if they’ve ever had dreams about the sort of picture that’s in the image above.  Spoiler: They totally have.

Q: What is the speed of entanglement?

A: Faster than the speed of thought, but slower than the speed of love.

Entanglement is sometimes described as a “superluminal effect” (an effect that travels faster than the speed of light).  In fact, nothing is traveling at all, which is good because superluminal stuff causes a whole mess of problems.  In the first example, way back at the beginning of this post, when Alice looks at her marble she’ll immediately know what Bob’s marble is.  But that’s just correlation.  No signal is sent, no information can be carried.

On the other hand, if the marbles are entangled, then they’re each in a (correlated) superposition of states.  So when Alice looks at her marble and sees, for example, “Blue” then Bob is guaranteed to see “Red”.  Bob’s marble is no longer in a superposition of states, it’s in just one.  This is the effect that seems to be traveling: Alice turns Bob’s two-state marble into a lonely-one-state marble.

But even that effect is illusory.  Like freaking everything weird in quantum mechanics, you can resolve this with the Many Worlds Interpretation.  Basically, not only are the marbles in multiple states, but the people are too.  By interacting with the marbles Alice and Bob become entangled with them.  Using fancy notation (where “” means “hasn’t looked yet”) the state of the entangled marbles and Alice and Bob is:

When Alice looks at marble 1, she will suddenly be entangled with her marble.  For example, the “Red” state becomes coupled with Alice’s “saw Red” state.  Likewise, Bob will become entangled with his marble when he interacts with (observes) it.

So, it’s not that some effect magically moves from one marble to the other, it’s just that the people involved “get caught up in the correlation”.  The state of “Alice sees Red” always coincides with the state “Bob sees Blue”, but no actual communication is necessary.  This weird transference of entanglement (where the entanglement between two particles causes other things to become entangled) is essentially how quantum teleportation works.  Also, and this is a subtle point, Alice and Bob have no way of noticing that they got the same result until they’ve at least had a chance to compare notes.  “Note comparing”, it’s worth noting, is always slower than light.

By the way, in very much the same way that correlation is boring and underwhelming, quantum teleportation is also pretty disappointing.  Nothing ever really gets teleported.  Total rip off.

Q: Is entanglement useful for anything?

A: Psh!  Yes!

Quantum computers are a total pain to get working, but if/when they do work, they’ll be able to do all kinds of things, like break encryption keys and simulate complex quantum mechanical systems, like protein folding.  Also (and this is the point) they require lots of entanglement.  So far, one of the big accomplishments of quantum computation is factoring the number 15.

It’s 5 times 3.

Today the killer app for entanglement is “quantum cryptography”.  The name is a little misleading.  It should be “quantum shared random secret generation”…  Having written that, I can see why everyone uses the first name.

The idea is; Alice and Bob get a whole bunch of entangled photons, then they each measure pairs one at a time.  Since the photons are entangled, Alice and Bob will always get the same result from their measurement, and the results will always be perfectly random.  So, Alice and Bob end up with identical, but perfectly random strings of 1’s and 0’s.  These can then be used as one time pads (the only perfect form of encoding).

The beauty and the curse of entanglement is that it’s easy to mess up.  When you interact with a particle that’s in multiple states, it ends up being in one state (from your perspective).  So, if anyone intercepts either entangled photon before it gets to where it’s going, the entanglement is broken (remember: entanglement means correlation and multiple states).  Alice and Bob will no longer get exactly the same results, and so they’ll detect that there’s a spy in their midst.  There’s a little more to it, but that’s the general idea.  Normal information can be copied, but quantum information (which includes entangled stuff) can’t.  This is called the “no cloning theorem“.

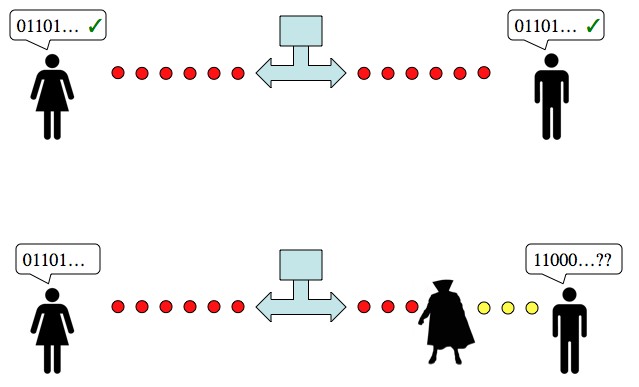
Quantum cryptography: two streams of entangled photons are created such that when measured they always have the same result, either a 1 or 0.  These streams are sent to Alice and Bob. If some Shadowy Figure (known as “Eve” in crypto circles) were to intercept one of the streams, that Shadowy Figure wouldn’t be able to replicate the entanglement, and Alice and Bob would find their random numbers don’t line up.

Right now the longest “quantum channel” is about 150 km long.  But, with some fancy tricks, like quantum error correcting, quantum teleportation, and really clean fiber optic cables, we may be seeing “quantum networks” in the relatively near future.

If you’ve made it this far, firstly: congrats, these were supposed to be short answers.  Secondly, if there’s an obvious entanglement question that was missed, let me know.  It’s easy enough to make long posts longer.