Physicist: This subtlety was one of the great insights of Newton; that the “falling apples” force and the “circling planets” force are one and the same.
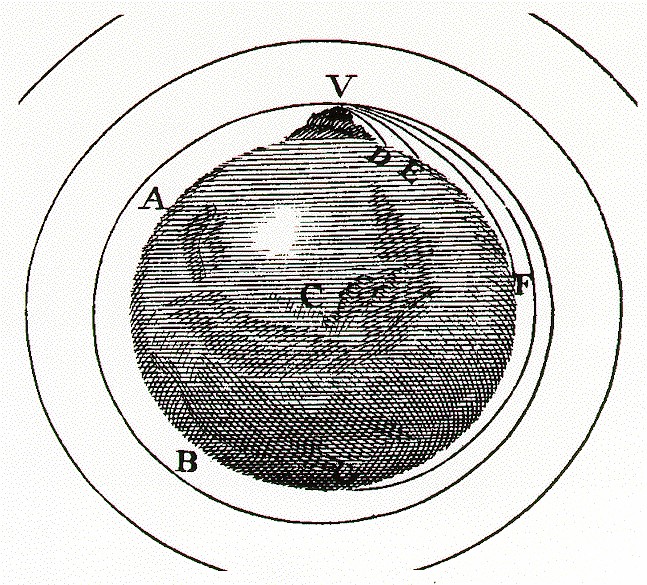
Newton's original thought experiment describing the parallels between falling and orbiting. The faster an object moves sideways the longer it stays aloft. Fast enough, and it never hits the ground at all.
Whether gravity pulls an object into orbit or just “makes it fall” depends on how the object is moving. Basically, every object wants to follow some kind of orbital path. If you toss a ball, even that ball is following an orbital path. If that path happens to intersect the ground, then we say “the object fell”. If that path doesn’t intersect the ground, then we say it’s in orbit.
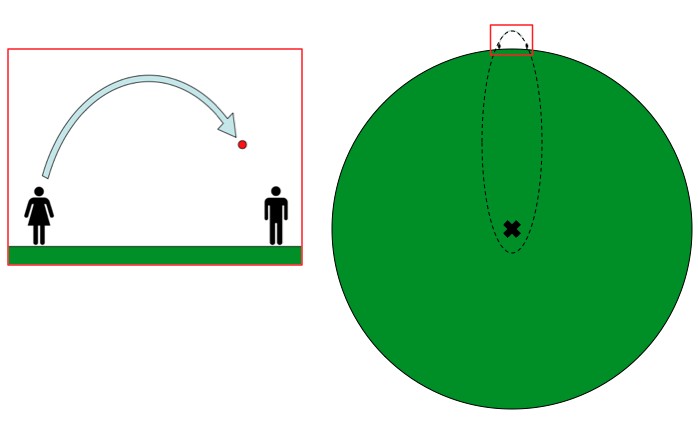
Anytime an object is in free-fall it's following an orbital path. Gravitationally speaking, until a thing hits the ground it can't tell the difference between the Earth and an Earth's worth of mass crammed into a point (black X).
When in free-fall, all that the ball “knows” is that there’s some gravity around. When it hits the ground it’s as surprised as anything else. The path that any tossed or falling object follows is just the tip of a very elliptical orbital path that, if the Earth’s mass were all crammed together in a point, would eventually bring the object back. Unless you were to throw the ball at a couple thousand mph, it would take about half an hour to complete the loop.
So the only difference between a satellite falling back to Earth and staying in orbit is whether or not the satellite’s orbital path intersects the surface of the Earth. So, Douglas Adams was right; “Flying is simple. You just throw yourself at the ground and miss.”







Follow-up question: if thrown objects make elliptical paths, then why do they appear to follow parabolic paths even over extreme distances where the elliptical-ness would seem to make itself more apparent? The equations I remember from undergrad physics suggest parabolic paths too, if I remember right. (I remember realizing this back then too, but I forgot about it before I actually asked what the answer was.)
Wait a minute, I think I just realized the answer like immediately after posting; it’s because of curvature, isn’t it? If the Earth was a perfectly flat plane, then it would be parabolic because the equations assume gravity is always pointing in the same direction at the source and destination over the entire path, and even over extreme distances (so long as they aren’t ballistic) you can model the Earth as essentially a flat plane. But over ballistic levels the curvature does become relevant, and so the path is elliptical rather than parabolic?
Exactly!
In fact, if you nail down one focus of an ellipse and let the other focus slide off to infinity, you end up with a parabola. While the center of the Earth (which is one focus of the orbit’s ellipse) isn’t infinitely far away, it’s still pretty far.
As often occurs in science, it’s a case of ‘for most practical purposes’
With gravity things fall __________.
Please help me with this fill I the blank on my homework I left school earlier whole we were watching a bill bye about gravity and I don’t know this answer cause I didn’t watch all of the video.
faster as they near the ground.
Pingback: “Truther” Don’t Understand Gravity | Truthers are Sanity Challenged
Something’s wrong about this. Why does the ellipse “end” just after it reaches the center of Earth? Shouldn’t the ellipse be extended to the opposite side of Earth? If not, explain this http://www.npr.org/templates/story/story.php?storyId=211434213.
@J.S.Partre
Great question!
The picture in this post is of the orbit of an object around an Earth’s worth of mass in a point. In this case that point is at the focus of a thin elliptical orbit.
The article you linked to is about and Earth’s worth of mass in an Earth’s worth of volume. In that case, as you fall into the Earth the layers above you cancel out and it just so happens that the result is “sinusoidal motion”.
Thanks, I didn’t expect to get the answer so fast! Could you please elaborate on what is “worth of [mass|volume]”? I didn’t quite get what is meant by that and Google didn’t help either.
@J.S.Partre
The amount of mass/volume that the Earth has.
heya
this is amazing how do you people know this?
How does the earth’s rotation and air resistance fit into this discussion?
@charles laMonica
If you’re in orbit, above the atmosphere, then the fact that the Earth is rotating and covered in air is completely unimportant. As far as being in orbit is concerned, the fact that the Earth exists and has mass is all that matters.
Earth’s rotational speed at the equator is about 1/16th the speed of something in low orbit, which isn’t insignificant. So space faring countries like to launch to the East (to add that speed to their rockets) and as close to the equator as possible (because the equator is where that speed is the greatest). Finally, because things go wrong, it’s best to launch over the ocean so that no humans get hit by failed launches (hence launching from Florida).