Q: Satellites experience less time because they’re moving fast, but more time because they’re so high. Is there an orbit where the effects cancel out? Is that useful?

The original question was: I read that due to time dilation from both gravity and speed, GPS satellites need their clocks adjusted to match Earth’s time or else the whole idea would fall flat on its face. So my question is wouldn’t there be a natural way to match the GPS clocks with Earth by simply having the time dilation from movement offset the time dilation from gravity? How fast would they have to orbit the Earth to cancel out the gravitational time dilation?

Physicist: That’s a really good question!  The thumbnail sketch of time dilation is: fast things and low things experience less time.  So satellites above our head experience a little more time because they’re high, but a little less because they’re moving.

Something orbiting at ground level (assuming you could orbit at ground level) would be tearing along at about 8 km/s: same height as us, and great speed, means slower in time.

Something orbiting very far away is moving pretty slow.  Great height and low-speed means faster in time.  Somewhere in between there’s an orbit where the effects cancel.

It turns out that a satellite would have to orbit at about the same speed it would hit the ground if it fell, straight down, from the height of that orbit.  That orbit is 50% of the radius of the planet above the surface of the planet.  In the case of Earth, that’s 1,975 miles up, well below the 12,600 mile altitude of the GPS network.  So, their on-board clocks run a little faster than identical ground-based clocks (a gain of about 1.7 seconds per century).

For the non-physicists out there, I can’t tell you how unusually straight forward that 50% radius thing is.  You almost never get results that clean.

To a very good approximation the gravitational time dilation can be calculated by using “moving” time dilation and plugging in the speed you’d be falling, if you fell from that height.

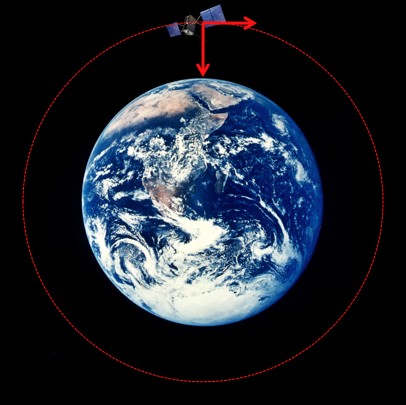
The time-slowing and time-speeding effects cancel at an orbital height of 50% of the planet’s radius.  At this altitude the orbital speed, and the speed with which you’d hit the ground falling from that height, are equal.

You can picture this in terms of someone at the higher location dropping clocks to someone at the lower location, who has an uncanny power to read speeding clocks.  The laws of physics, including the ones regarding time, act more or less the way they “should” in a zero-g environment.  For example, in zero gravity if you knock a cup off of a table it doesn’t start magically moving (falling) for no reason.  Impossible!  The falling clocks are basically carrying an accurate record (not needing to worry about gravity) of the time frame from which they started falling.

At least that’s one method of calculating general relativistic time weirdness.  A better (but equivalent) one is here.

As for fixing the problem: no problem.  Relativity, although difficult to wrap your head around, is no mystery.  We know exactly how fast time is passing for every satellite in the sky.  To deal with it, all that’s needed is clocks that run at a slightly different rate.  The specifics can be found on page 7 of this.  Building a clock to keep a very particular “incorrect” time is exactly as difficult as building a clock to keep “correct” time.  No problem.

Answer Gravy: The “general relativity can be approximated by using special relativity and how fast things fall” works well so long as the gravity isn’t really messing up spacetime.  Basically, it doesn’t work on black holes, but it works great for planets and stars.  Once you figure out how fast something would be falling between two levels, you plug that into the “gamma function”, γ, which tells you how many times faster time is traveling at the higher level than the lower.

The speed, v, that an object with mass, m, will be going if it falls from somewhere in space, R, to ground level, r, can be found by looking at the difference in gravitational potential energy and setting that equal to the gain in kinetic energy: .

This speed, v_g, is what you use to find how much time is going faster for the satellite.

The speed of a (circular) orbit can be found by setting the gravitational force equal to centrifugal: .  This speed, v_s, is what you plug in to find how much time is going slower.

In general the speed of the clocks on a satellite is faster than clocks on the ground by a factor of .  However, in this case we’re looking for the overall factor to be 1 (time is the same for the satellite as the ground).  So, v_g = v_s.

For v_g: .

For v_s: .