Q: How is radiometric dating reliable? Why is it that one random thing is unpredictable, but many random things together are predictable?

Posted on May 12, 2012 by The Physicist

The original question was: Suppose there is a set of variables whose individual values are probably different, and may be anything larger than zero. Can their sum be predicted? If so, is the margin for error less than infinity?

This question is asked with the intention of understanding basically the decay constant of radiometric dating (although I know the above is not an entirely accurate representation). If there is a group of radioisotopes whose eventual decay is not predictable on the individual level, I do not understand how a decay constant is measurable. I do understand that radioisotope decay is modeled exponentially, and that a majority of this dating technique is centered in probability. The margin for error, as I see it presently, cannot be small.

Physicist: The predictability of large numbers of random events is called the “law of large numbers“.  It causes the margin of error to be essentially zero when the number of random things becomes very large.

If you had a bucket of coins and you threw them up in the air, it would be very strange if they all came down heads.  Most people would be weirded out if 75% heads of the coins came down heads.  This intuition has been taken by mathematicians and carried to its more difficult to understand, and convoluted, but logical extreme.  It turns out that the larger the number of random events, the more the system as a whole will be close to the average you’d expect.  If fact, for very large numbers of coins, atoms, whatever, you’ll find that the probability that the system deviates from the average by any particular amount becomes vanishingly small.

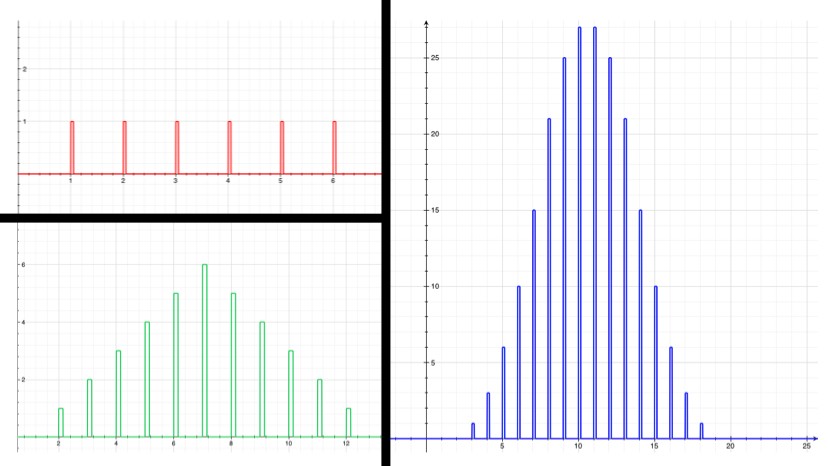
For example, if you roll one die, there’s an even chance that you’ll roll any number between 1 and 6.  The average is 3.5, but the number you get doesn’t really tend to be close to that.  If you roll two dice, however, already the probabilities are starting to bunch up around the average, 7.  This isn’t a mysterious force at work; there are just more ways to get a 7 ({1,6}, {2,5}, {3,4}, {4,3}, {5,2}, {6,1}) than there are to get, say, 3 ({1,2}, {2,1}).  The more dice that are rolled and added together, the more the sum will tend to cluster around the average.  The law of large numbers just makes this intuition a bit more mathematically explicit, and extends it to any kind of random thing that’s repeated many times (one might even be tempted to say a large number of times).

The exact same kind of math applies to radioactive decay.  While you certainly can’t predict when an individual atom will decay, you can talk about the half-life of an atom.  If you take a radioactive atom and wait for it to decay, the half-life is how long you’d have to wait for there to be a 50% chance that it will have decayed.  Very radioactive isotopes decay all the time, so their half-life is short (and luckily, that means there won’t be much of it around), and mildly radioactive isotopes have long half-lives.

Now, say the isotope “Awesomium-1” has a half-life of exactly one hour.  If you start with only 2 atoms, then after an hour there’s a 25% chance that both have decayed, a 25% chance that neither have decayed, and a 50% chance that one has decayed.  So with just a few atoms, there’s not much you can say with certainty.  If you leave for a while, lose track of time, and come back to find that neither atom has decayed, then you can’t say too much about how long it’s been.  Probably less than an hour, but there’s a good chance it’s been more.  However, if you have trillions of trillions of atoms, which is what you’d expect from a sample of Awesomium-1 large enough to see, the law of large numbers kicks in.  Just like the dice, you find that the system as a whole clusters around the average.

If there’s a 50% chance that after an hour each individual atom will have decayed, and if you’ve got a hell of a lot of them, then you can be pretty confident in saying that (by any reasonable measure) exactly half of them have decayed at the end of the hour.

In fact, by the time you’re dealing with a mere one trillion atoms (a sample of atoms too small to see on a regular microscope), the chance that as much as 51% or as little as 49% of the atoms have decayed after one half-life (instead of 50%) is effectively zero.  For the statistics nerds out there (holla!), the standard deviation in this example is 500,000.  So a deviation of 1% is 20,000 standard deviations, which translates to a chance of less than 1 in 1086858901.  If you were to see a 1% deviation in this situation, take a picture: you’d have just witnessed the least likely thing anyone has ever seen (ever), by a chasmous margin.

Using this exact technique (waiting until exactly half of the sample has decayed and then marking that time as the half-life), won’t work for something like Carbon-14, the isotope most famously used for dating things, since Carbon-14 has a half-life of about 5,700 years.  Luckily, math works.

The amount of radiation a sample puts out is proportional to the number of particles that haven’t decayed.  So, if a sample is 90% as radioactive as a pure sample, then 10% of it has already decayed.  These measurements follow the same rules; if there’s a 10% chance that a particular atom has decayed, and there are a large number of them, then almost exactly 10% will have decayed.

The law of large numbers works so well, that the main source of error in carbon dating comes not from the randomness of the decay of carbon-14, but from the rate at which it is produced.  The vast majority is created by bombarding atmospheric nitrogen with high-energy neutrons from the Sun, which in turn varies slightly in intensity over time.  More recently, the nuclear tests in the 50’s caused a brief spike in carbon-14 production.  However, by creating a “map” of carbon-14 production rates over time we can take these difficulties into account.  Still, the difficulties aren’t to be found in the randomness of decay which are ironed out very effectively by the law of large numbers.

This works in general, by the way.  It’s why, for example, large medical studies and surveys are more trusted than small ones.  The law of large numbers means that the larger your study, the less likely your results will deviate and give you some wacky answer.  Casinos also rely on the law of large numbers.  While the amount won or lost (mostly lost) by each person can vary wildly, the average amount of money that a large casino gains is very predictable.

Answer Gravy: This is a quick mathematical proof of the law of large numbers.  This gravy assumes you’ve seen summations before.

If you have a random thing you can talk about it as a “random variable”.  For example, you could say a 6-side die is represented by X.  Then the probability that X=4 (or any number from 1 to 6) is 1/6.  You’d write this as P(X=4) = \frac{1}{6}.

The average is usually written as μ.  I don’t know why.  For a die, \mu = 1\frac{1}{6}+2\frac{1}{6}+3\frac{1}{6}+4\frac{1}{6}+5\frac{1}{6}+6\frac{1}{6} = 3.5.  This can also be written, \mu=\sum_n nP(X=n), and often as E[X].  E[X] is also called the “expectation value”.

There’s a quantity called the “variance”, written “σ2” or “Var(X)”, that describes how spread out a random variable is.  It’s defined as \sigma^2= \sum_n (n-\mu)^2P(X=n).  So, for a die, \sigma^2= (1-3.5)\frac{1}{6}+(2-3.5)\frac{1}{6}+(3-3.5)\frac{1}{6}+(4-3.5)\frac{1}{6}+(5-3.5)\frac{1}{6}+(6-3.5)\frac{1}{6}=2.91666...

If you have two random variables and you add them together you get a new random variable (same as rolling two dice instead of one).  The new variance is the sum of the original two.  This property is a big part of why variances are used in the first place.  The average also adds, so if the average of one die is 3.5, the average of two together is 7.  So, if the random variables are X and Y with averages μX and μY, then μ=μX+μY.  And using expectation value notation (if you’re not familiar look here, or just trust):

\begin{array}{ll}Var(X+Y)\\= E[(X+Y-\mu)^2]\\= E[(X+Y-\mu_X-\mu_Y)^2]\\= E[((X-\mu_X)+(Y-\mu_Y))^2]\\= E[(X-\mu_X)^2]+2E[(X-\mu_X)(Y-\mu_Y)]+E[(Y-\mu_Y)^2]\\=Var(X)+2E[(X-\mu_X)]E[(Y-\mu_Y)]+Var(Y)\\=Var(X)+Var(Y)+2(E[X]-\mu_X))(E[Y]-\mu_Y)\\=Var(X)+Var(Y)+2(0)(0)\\=Var(X)+Var(Y)\end{array}

You can extend this, so if the variance of one die is Var(X), the variance of N dice is N times Var(X).

The square root of the variance, “σ”, is the standard deviation.  When you hear a statistic like “50 plus or minus 3 percent of people…” that “plus or minus” is σ.  The standard deviation is where the law of large numbers starts becoming apparent.  The variance of lots of random variables together adds, Var(X+\cdots+X) = N\cdot Var(X), but that means that \sigma_{x+\cdots+x} = \sqrt{Var(X+\cdots+X)} = \sqrt{N\cdot Var(X)}=\sqrt{N}\sigma_x.  So, while the range over which the sum of random variables can vary increase proportional to N, the standard deviation only increases by the square root of N.  For example, for 1 die the numbers can range from 1 to 6, and the standard deviation is about 1.7.  10 dice can range from 10 to 60 (10 times the range), and the standard deviation is about 5.4 (√10 times 1.7).

What does that matter?  Well, it so happens that a handsome devil named Chebyshev figured out that the probability of being more that kσ from the average, written “P(|X-μ|>kσ)”, is less than 1/k2.  Explanations of the steps are below.

\begin{array}{ll}i)&P(|X-\mu|>k\sigma)\\ ii)&=\sum_{|n-\mu|>k\sigma} P(n)\\iii)&\le\sum_{|n-\mu|>k\sigma} \frac{|n-\mu|^2}{k^2\sigma^2}P(n)\\iv)&=\frac{1}{k^2\sigma^2}\sum_{|n-\mu|>k\sigma} |n-\mu|^2P(n)\\v)&\le\frac{1}{k^2\sigma^2}\sum_n |n-\mu|^2P(n)\\vi)&\le\frac{1}{k^2\sigma^2}\sigma^2\\vii)&=\frac{1}{k^2}\end{array}

i) “The probability that the variable will be more than k standard deviations from the average”.  ii) This is just re-writing.  For example, if you have a die, then P(X>3) = P(4)+P(5)+P(6).  This is a sum over all the X that fit the condition.  iii) Since the only values of n that show up in the sum are those where |n-μ|>kσ, we can say that 1<\frac{|n-\mu|}{k\sigma} and squaring both sides, that 1<\frac{|n-\mu|^2}{k^2\sigma^2}.  Multiply each term in the sum by something bigger than one, and the sum as a whole certainly gets bigger.  iv) “1/k2σ2” is a constant, and can be pulled out of the sum.  v) If you’re taking a sum and you add more terms, the sum gets bigger.  So removing the restriction and summing over all n increases the sum.  vi) by definition of variance.  vii) Voilà.

So, as you add more coins, dice, atoms, random variables in general, the fraction of the total range that’s within of kσ of the average gets smaller and smaller like \frac{1}{\sqrt{N}}.  If the range is R and the standard deviation is σ, then the fraction within kσ is \frac{k\sqrt{N}\sigma}{NR} = \frac{1}{\sqrt{N}}\frac{k\sigma}{R}.  At the same time, the probability of being outside of that range is less than 1/k2.

So, in general, the probability that you’ll find the sum of lots of random things away from their average gets very small the more random things you have.

This entry was posted in -- By the Physicist, Combinatorics, Math, Particle Physics, Probability. Bookmark the permalink.

9 Responses to Q: How is radiometric dating reliable? Why is it that one random thing is unpredictable, but many random things together are predictable?

  1. thebloggiest says:
    May 12, 2012 at 3:53 pm

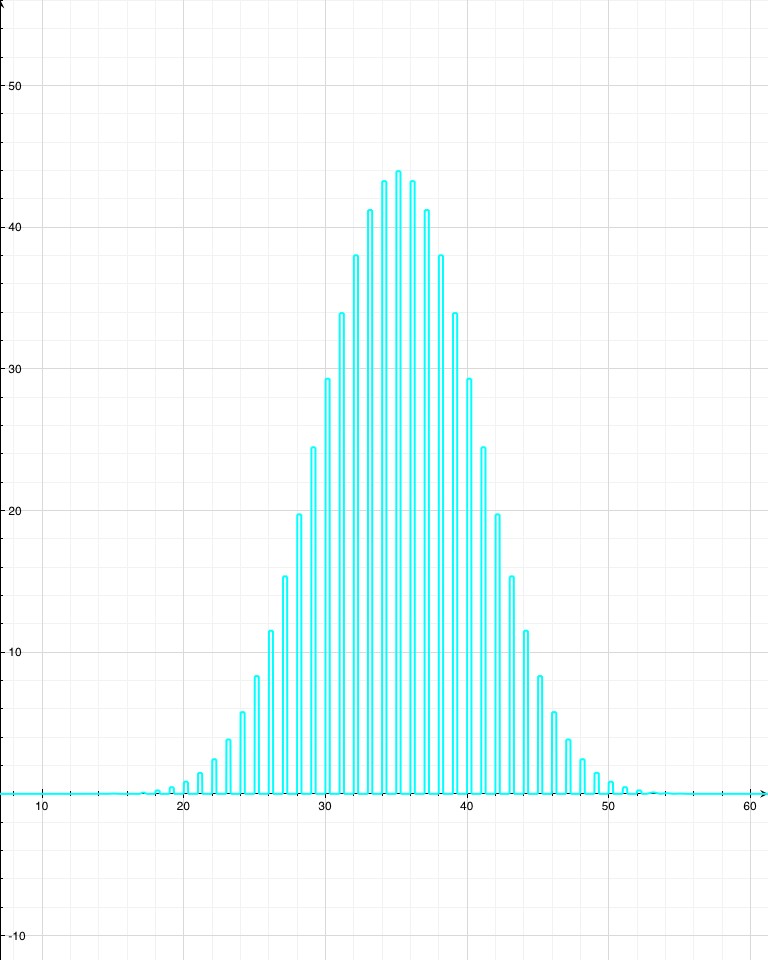
    Since radioactive decay is a normal distribution, shouldn’t the probability of being 20000 standard deviations away be much smaller? On a normal distribution, 8 s.d. out is essentially zero. According to Wolfram Alpha, 20000 s.d. out happens one time in 10^86858901.

  2. Error: Unable to create directory uploads/2024/12. Is its parent directory writable by the server? The Physicist says:
    May 13, 2012 at 5:00 pm

    You are absolutely right!
    My estimation was lazy. Fixed!

  3. Edward Ingram says:
    June 19, 2012 at 8:26 am

    I understand the statistical argument given. I would approach the question another way, though.
    I looked up the half life of U238 and it was given as 447 billion years.
    How do we know that the decay RATE will remain constant?
    Couldn’t it change? Since there is so much time involved, how can we say that some process or force will not develop that could speed up or slow down the decay rate?

  4. Pingback: One-third of Americans reject evolution, poll shows - Page 7 - Defending The Truth Political Forum

  5. Brian says:
    January 7, 2014 at 1:59 pm

    How do we know that decay is proportional, linear, geographic, logarithmic or otherwise?
    If the half-life of an atom is 1 hour, it should be gone withing 24 hours, but with a statistically large number of atoms, this wouldn’t necessarily be the case. With 1 billion atoms, this becomes 500M after 1 hour, 250M after 2, 125M after 3, 75M after 4 and so on until after 24 hours we’d expect to see roughly 60 atoms left. If they didn’t decay linearly but faster, i’d expect them to be all gone something like, 50% at 1 hour, 75% of all remaining decay at 2 hours, 88% of all remaining at 3 hours and so on.

    Since we can’t observe decay on these large scales, why do we assume they’re linear? If we liken it to how humans age, we can see that the average age of people are roughly 75 years at death, but at some point there is a limit ~120 years. We can’t apply a half-life progression to life-expectancy or we should have a couple 200 year olds out there. Why don’t we expect atoms to decay as such?

    Thanks,

    Brian

  6. Leo Freeman says:
    May 12, 2014 at 8:00 am

    The fact that different isotopes decay at different rates seems to suggest that atoms are somehow aware of the passage of time. What process inside an atomic nucleus sets the particular probability of decay for that particular isotope? Does it mean that atoms have some sort of internal “clock” or “timer”?

  7. Error: Unable to create directory uploads/2024/12. Is its parent directory writable by the server? The Physicist says:
    May 12, 2014 at 9:00 am

    @Leo Freeman
    The shape of the “energy hump” that the nucleus needs to get over to fall apart is what determines the probability that an atom will fall apart in any given time interval. However, it doesn’t seem as though atoms change at all over time (don’t have clocks) because if they don’t fall apart, they “reset the clock”. That is, the chance that an atom will fall apart today is exactly the same as the chance that it will fall apart tomorrow (assuming it didn’t fall apart today and is still around).

  8. Leo Freeman says:
    May 14, 2014 at 3:04 am

    Thank you for your answer, but I still wonder about the statement that “the chance that an atom will fall apart today is exactly the same as the chance that it will fall apart tomorrow”. It still seems to suggest the need for some kind of internal timing device.
    I imagine an atom is like a casino, which will blow up when a roulette player inside lands the ball on a certain booby-trapped number. I think the act of spinning the wheel is a time-linked event, as the probability of the house blowing up on any particular day depends on the number of times the player rolls on that day. In order to keep the probability constant each day, wouldn’t the player needs to be able to accurately measure a 24-hour period and spin the wheel the required number of times?

  9. Pingback: A Bíblia e a Ciência contra o Darwinismo – alpharj

Leave a Reply

Your email address will not be published.