The original questions were:
How can quantum computers actually be more useful if we cannot observe superposition, since trying to harness two states at once would just produce one state?
Quantum Physics … is so full of uncertainty and Einstein didn’t like “God playing dice with the world.” How would you explain that quantum physics has today led to the development of the most accurate theories we have till date?
Physicist: Whether a quantum system is random or not kinda depends on what you’re taking about. For example, the electrons in an atom show up in “orbitals” that have extremely predictable shapes and energy levels, and yet if you were to measure the location of an electron within that orbital, you’d find that the result is pretty random.
One of the great victories of quantum mechanics was to prove, despite Einstein’s scoff to the contrary, that God does play dice with the world. Everything in the universe is in multiple states, but when a thing is measured it’s suddenly found to be in only one state (technically; a smaller set of states). Setting aside what a measurement is and what measurements do, the result of a measurement (the state that a thing will be found in) is often, but not always, fundamentally random and unpredictable.
For example, when a beam of light passes through a beam splitter the beam splits (hence the name) into two beams of half the intensity. In terms of waves this is pretty easy to explain; some of the wave’s energy goes through, and some reflects off of the splitter. In quantum theory you continue to describe light (and everything else) as a wave, even when you turn down the light source so low that there’s only one photon passing by at a time.
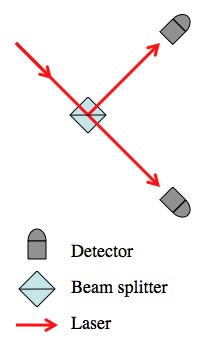
According to quantum theory (and verified by experiment) there is no way to predict which direction a photon will take through a beam splitter. This situation is "irreducibly random".
So, in exactly the same way that you’d mathematically describe a wave as going through and being reflected, you also describe the photon as both going through and being reflected. Place a pair of detectors in the two possible paths and you’re making a measurement. Suddenly, instead of taking both paths at the same time, the photon is found on only one (indicated by which detector detects), and there is absolutely no way to predict which path that will be.
So on the face of it, that seems like it should be the end of the road. There’s an irreconcilable randomness to the measurements of quantum mechanical systems. In the example above (and millions of others like it) it is impossible to make an accurate prediction. But keep in mind; it is possible to be clever.
The quantumy description of each photon going through the beam splitter isn’t a simple as “it’s totally random which path it takes”. Each photon is described, very specifically and non-randomy, as taking both paths.
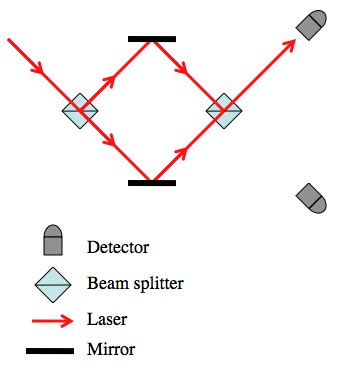
By properly adjusting the path lengths you can make it so that all of the photons go to a single detector. You can't predict which path the photon takes, but you can perfectly predict the end result.
Take the same situation, a laser going through a beam splitter, and add a little more to the apparatus. With a couple mirrors you can bring the two paths back together at another beam splitter. The light waves from both paths split again at the second beam splitter, but when you’re looking at the intensity of what comes out you have to take into account how the light waves from the two paths interfere.
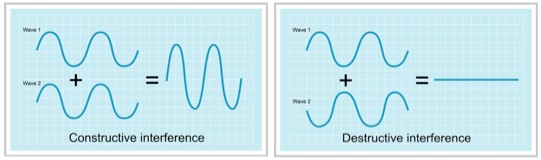
When waves are combined they don't simply add, they interfere. The sum of two waves can be larger (constructive interference) or smaller (destructive interference) depending on how they line up.
By carefully adjusting the distances you can cause one path to experience complete destructive interference, and the other to experience complete constructive interference. This is all fine and good for a laser beam, but when you turn down the intensity until there’s only one photon passing through at a time, you still find that (in the example pictured) only the top detector will ever be triggered. This isn’t “theory” by the way, it’s pretty easy to set this up in a lab.
This is a little spooky, so take a moment. The quantum theory description is that a single photon will take both paths. If detectors are placed in the two paths it is impossible to predict which will fire. But if the paths are recombined, we can see that the photon took both paths, because it interferes with itself in a very predictable way, and produces very predictable results. If, instead, we took the “quantum mechanics says things are random” tack we’d expect that at each beam splitter the photons made a random choice, and the detectors in the second example would each fire half the time.
So quantum theory can predict that an event will be random, or in other situations it can accurately predict the outcome (even though that prediction sometimes seems impossible). It all comes down to a judicious application of measurements and how you allow the quantum system to interact with itself.
This particular example can be extended to allow for “interaction free measurements“, which seem impossible, but are in fact just another (accurate) prediction of quantum mechanics. The non-randomness of quantum mechanics is the basis of quantum algorithms, and (in a less direct way) is why chemistry “works”.







Nice article, thanks for doing what you do.
But I didn’t get the “But if the paths are recombined, we can see that the photon took both paths, because it interferes with itself in a very predictable way, and produces very predictable results”.
Can you elaborate more on why the wave interference leads to a predictable result?
The “very predictable result” is that the light (in this case) always goes up at the second beam splitter. A single beam always splits at a beam splitter, but two beams can interfere and result in all of the photons coming out in only one direction.
This is about the clearest and most concise explanation of this phenomenon that I have read anywhere. Thanks! It makes me think that when a single photon is simultaneously on two “separate” paths this must meant either 1) the photon has a ghostly doppelganger at the other location (probably an erroneous way of thinking about it), or 2) one object at two locations in spacetime may imply an enigma about spacetime itself, i.e., that it on some level the two spacetime loci aren’t really separate. Pardon me for writing while I am thinking through it.
The idea of a “ghost particle” taking the other path is kinda similar to the idea of “pilot wave theory”, which describes particles as “scouting ahead” on every possible route before choosing which one to take. Pilot wave theory is largely rejected by the physics community.
In general, every problem with quantum mech (that I’ve encountered) can be cleared up really well by thinking of everything in terms of waves (that have some strange properties) instead of as particles. Among other things, you don’t have to worry about things needing to be in a particular place or not.
Ok… Apologies for this sounding like a stupid question, but may I ask, why waves? I certainly don’t dispute it and in fact completely agree, but I can’t shake the question of why a wave is? Perhaps I’m trying to ask what the context is in which the waves propagate themselves? If the vacuum of space is in a non-zero state, then what is the ‘stuff’ that makes it non-zero? and how does this relate to waveform geometry?
In modern physics, when something is called a “wave” it’s more of description of its properties than it is a statement of fact. That is to say, when most people talk about waves it’s assumed that there’s a material involved that’s doing the waving, but in quantum mechanics when we say that something is a wave what we’re really saying is that there are frequencies involved, and interference, and propagations, and all the usual wave stuff.
So the nature of the vacuum state isn’t particularly important to the behavior of most other quantum mechanical systems, because the question of “what the wave is made of” isn’t really a valid question.
Agreed, but it still feels somewhat coldly instrumentalist, as it removes any discussion of context from the argument. Certainly, the properties can be quantified as waves, however the behaviour of something would normally (and quite reasonably) be considered an emergent trait in relation to or influenced by what surrounds it (an inversion so to speak). The above argument presents a wave as the context to the behaviour of a photon, but doesn’t provide any context as to the behaviour of the wave, and it’s hard not to feel a bit uncomfortable with this.
how does the beam splitter work?
Science is the true light we need tnx for this great article
please please keep up this great work of yours
I’m a bit late to the party, but I wanted to clarify something for myself.
In example two, where only one detector will receive the photon is it that every photon will arrive at the detector, or that the ones that “would” arrive at the other detector interfere with themselves and don’t register with it?
I guess, basically, I want to know whether the destructive interference simply makes the photon “vanish” for the detector, while still taking that path, or whether it renders that “possible” path impossible for the photon to take BECAUSE it would be nullified.
Thank you.
If observation locks the state of a quantum (whatever), one that is no longer under observation does its state return to random once it is no longer observed. If that is the case does that mean that observation imposes the actual state? Would that also mean that the quantum unit is not random it is just existing in an everything at once state, until observations happens. If that is right it sounds like observation is just a sort of filtering of every state that the observer is unable to “observe”.
Pingback: A finely tuned universe that points to a God. - Page 26 - Christian Forums
Hello,
Je pense que si vous concluez que la mécanique quantique dit que “tout est aléatoire”, je pense que vous n’avez rien compris à celle-ci, car ce n’est absolument pas le cas.
Ce qui est dit, c’est qu’il n’y a que des champs quantiques, qui subisse localement en cas d’interaction, une réduction du paquet d’onde. Cette réduction SEMBLE aléatoire. Ça veut dire qu’on est incapable de donner autre chose qu’une probabilité. Mais la vérité c’est qu’aucun scientifique ne sait aujourd’hui qu’es ce qui choisit.
Certains disent le hasard pur, mais ça n’a aucun sens. Un peu comme dire qu’il y avait le néant avant l’univers. Le néant, par définition ne peut pas créer. Le hasard ne peut pas choisir.
En réalité, il s’agit juste des limites de notre savoir. Il y a très certainement une mécanique et des lois qui permettent d’expliquer le choix fait lors de la réduction du paquet d’onde. Reste à la comprendre…
_______________________ GOOGLE TRAD _______________________
I think if you conclude that quantum mechanics says that “everything is random,” I think you do not understand it, because this is absolutely not the case.
What is said is that it is only quantum field, which undergoes locally when interacting, a wave function collapse. This reduction LOOKS random. That means we can not give anything but a probability. But the truth is that no scientist knows today what art chooses.
Some say the chance, but it makes no sense. A bit like saying that there was nothing before the universe. Nothingness, by definition can not create. Chance can not choose.
In reality, this is just the boundaries of our knowledge. There are certainly mechanical and laws that explain the choice made during the wave function collapse. It remains to understand …