Physicist: This is a really nasty, complicated question. It’s isn’t remotely straight-forward in the way that adding spacial dimensions is. The universe we live in is “3+1 dimensional”, meaning 3 spacial dimensions and one temporal dimension. While time and space do have more in common than you might think, they are still (no surprise) fundamentally different.
Because we live in a 3-D space, when we talk about what life is like in higher (spacial) dimensions we’re free to extrapolate from what we know life would be like in one dimension, how that changes when you move up to two dimensions, and how things are further generalized in three dimensions. We can expect those patterns to continue into higher dimensions (example here!). We’re even free to laugh haughtily at the pitiable denizens of a hypothetical one-dimensional world who are incapable of seeing how things behave in 2 or 3 dimensions.
Well, in terms of time that’s exactly the situation we’re in. In the same way that a one-dimensional critter can know everything about where they are with a single number (like points along a ruler), a one time-dimensional critter (for example, everyone and everything) can know everything about when it is with a single number. The fact that we use several numbers to designate time is an indulgence.

Having different numbers for the year, month, and day makes this solid gold calendar an indulgence. These numbers can be lumped together into just one number, because there’s only one time dimension.
Going from talking about points on a line (1-D) to talking about points in a plane (2-D) is a huge leap. Suddenly have to concern yourself with trigonometry. In a 3+2 dimensional universe, “temporal cartographer” could be a real job, and the working day would be “9 to 5 by 9 to 5”.
I wish I could offer up a reasonable guess about what life would be like with multiple time dimensions. But just as a 1-D person can’t conceive of turning around, I can’t say what it means to “turn corners in time”. Normally when presented with “what if” questions, you can ponder it in terms of how the laws of physics would change the least. In this case they’re entirely up in the air. For example, in physics it’s sometimes important to show that the past and future are different “places”. This is so “obvious” that we take it for granted. Regular rotations give us a way of “translating” any point into any other point that’s the same distance away. That is; if you’re looking at something and you turn around, then that thing is behind you (physics is full of profound truisms like that). Special relativity has provided us with another kind of “rotation” that exchanges some of one of the space directions with some of the time direction, but in a not-quite-as-simple way that involves a new kind of distance.
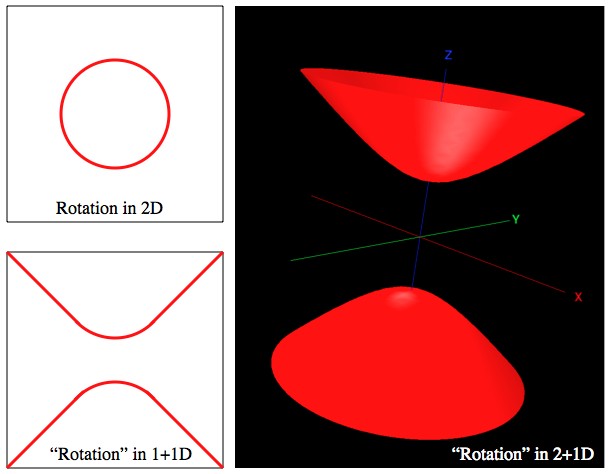
The set of points that are a fixed distance from the center in 2 D, in 1+1 D, and in 2+1 D. Rotations can slide things around, but they don’t change distance. Notice that a point in the future can slide around in the future, but it lives on a different “sheet” than a point in the past.
In regular space you can rotate, and in so doing, the relative position of everything around you traces out a circle. In particular, things in front of you can end up behind you (Try it! This post can wait.). Rotation is just an interchanging of two space directions. With special relativity comes the idea of the “Lorentz boost”, which is just a fancy way of saying “space-and-time rotation”. When you go from sitting still to riding on a train, you’ve undertaken a Boost. In the same way that physically turning around rearranges where things are (with respect to you), a Boost rearranges where and when events take place (with respect to you). For example, when you’re not riding the train it shows up in lots of places at different times, but when you do ride it, it only shows up in one place at different times. However, and this is the important part, the Lorentz Boost can’t take an event that’s in your future and rotate it into your past, or vice versa.
However! With another time direction comes a new kind of rotation. Ordinary rotation is an interchange of two space directions, Boosts are an interchange of a space direction and the time direction, and in 3+2 D space you can have a rotation that exchanges the two time directions. Importantly, this new rotation can smoothly take events in your future and take them into your past. That is to say; in 3+2 dimensional space you should be able to “turn around in time” and face the past.
I have no idea what that means.
It may be the case that some of our physical laws are symptoms of the dimension we live in. For example, in a 1+1 D universe you’d have “conservation of directionality”, because nothing can turn around. In our 3+1 D universe the fact that particles are only Fermions or Boson can be tracked back to the fact that we live in more than two (spacial) dimensions (very complicated details here). However, there may be a lot of “laws” that are caused, at least in part, by the restrictions placed on us by the single time dimension we have to work with.
So, unfortunately, there are no actual answers to what the world would be like with more time dimensions, but (since it has nothing to do with reality) there’s no hurry to find those answers.
Answer gravy: Many of the most basic laws involve equations that are “ill-posed” in multiple time dimensions, and either don’t have solutions, or don’t make sense. Almost every law in physics is written in terms of cause and effect, initial conditions to later conditions. Extending that doesn’t sound terrible. It seems like you could just extend the laws we have now, the same way you can for spacial dimensions, to work the same on each time direction the same way it does for just one. But the laws we work with in physics just don’t extend in any useful way into higher dimensions without tacking on lots of weird extra restrictions that, in all but name, bring you back to a 3+1 dimensional universe.
The result of the initial conditions from one time direction will usually disagree with the initial conditions on the other times. No matter how you define the initial conditions (what “initial” means in multiple time dimensions is an issue in itself), you’ll find that the initial conditions always cut across “characteristic lines”, which (this is not obvious) lead to a lack of solutions in general. “Characteristic lines” are the paths that solutions to an equation “propagate along”, and having initial conditions on them basically means putting more information onto what should already be a solved problem.
For example, the sound that a speaker generates can be described easily using basic acoustic laws: the sound created by the speaker (initial condition) leads naturally to an easily calculable sound everywhere else (final conditions). However, the sound created by a speaker traveling at the speed of sound, cannot be easily calculated, because the sounds the speaker makes all “stack up”; the speaker is continuing to make new sound on characteristic lines. There are ways to deal with this, but they’re not “basic”, and required a lot more research. The same mathematical complications crop up in effectively everything when multiple time dimensions are considered.
There’s a paper here that considers some workarounds in detail.







I imagine having a mind with more than 1 dimension of time available to it would result in some kind of gestalt that exists in multiple states and possibilities at the same time. Perhaps you’d end up with a mind that exists on multiple independant timelines (like having multiple bodies?) or perhaps you’d end up with a mind that exists in all ‘past’ and ‘future’ states at the same time. Or perhaps you’d end up with something wierder.
Whatever you’d get, it would be extremely interesting to compare to ourselves.
While I was reading this post, I turned around, and what was in front of me ended up BEHIND ME.
Very interesting concept.
The system works!
If you get shipwrecked, end up on an island, how do you determine your
position? Without fancy maths, otherwise I’ll
be stranded there till the day I die. And you would be blamed 🙂
If you’re in the northern hemisphere you can find the north star and the angle between it and the horizon will be equal to your latitude. In the southern hemisphere you just find the patch of stars that move the least (it’s near the Southern Cross).
Sadly, without accurate clocks there’s no way to determine your longitude. This was a pretty serious issue way back in the day, and led to people building telescopes to look at the moons of Jupiter (which were the next best thing).
I would have thought you’d be able to get an approximate estimation of longitude with a decent sundial.
That tells you what the local time is, but it doesn’t tell you the time relative to somewhere else, which is what you need to know your longitude relative to somewhere else.
Ah yes, I see.
Hmm, it never occured to me how difficult it is to determine longitude without a clock.
Sorry if you covered this in your post (I may have skimmed a paragraph or two….), but the minimal N+2 spacetime would be one where the time dimensions are orthogonal and can’t talk via boosts. So each particle would in principle have two clocks associated with them. This isn’t as interesting as expanding the normal time dimensionality.
In fact, does anyone know the experimental limits on the size of a small extra time dimension? (I guess coupling to the regular metric is an unknown parameter as well…)
You would need two “clocks” (that would be very different from normal clocks) and the time dimensions couldn’t be exchanged by “boosts”, by they would be able to “communicate” in the same sense that spacial dimensions can communicate through rotations.
If you’re thinking of an extra “toroidal dimension” (tiny extra direction that loops back on itself), then it would need to be small enough to go unnoticed. So… less than 10-18 meters?
Perhaps the splitting/merging tracks of possibility described by the Many Worlds Interpretation of QM might be thought of as existing in one or more additional temporal dimensions. Quantization prevents smooth continuous rotation through any such extra time dimension producing the discrete “splitting” effect instead.
I have been wondering if an extra time dimension might explain the weirdness we see at the quantum level. The quantum leap of electrons between orbits might be an electron travelling along the T2 axis (perpendicular to our familiar T1 axis), so moving in space but appearing to do so instantaneously from the perspective of our T1. Or particles appearing to be everywhere at once could be that they move along the T2 axis too (e.g. diagonally in the T1-T2 plane). And it could explain how entangled particles communicate instantaneously (in our T1) across distances. Now, if I could just devise an experiment… 🙂
On science channel there was a scientist talking about this. It seemed he was researching if a 3 dimensions of time (so 3 and 3) might help explain what time actually is or quantum mechanical things. To develop a testable model that answers questions and has predictive power is hard enough, but I remember him echoing what the physicist says here; the math behind a 3+3 universe is dauntingly complex, and nothing makes sense or is intuitive (because we are 3+1 creatures). I wish him luck on his intrepid research!
How smooth is the black hole event horizon? Does it have ripples due to objects in orbit just beneath the event horizon? Would detecting such ripples count as a way information could leave a black hole?
This little video does an EXCELLENT job of explaining how there could be SIX temporal dimensions.
http://www.tenthdimension.com/flash2.php
Semi-unrelated to that, it occurs to me that when you represent a timeline, you draw a one-dimensional line. When you then represent an ALTERNATE timeline (because you’re a time traveler who changed the past – see Back to the Future 2 where the Doc explains that they have to go back to 1955, not 2015, to undo Biff’s changes to the present), you draw a second line next to it… in the 2nd dimension. Same for if you draw a time loop. You need that second dimension in order to illustrate and explain it.
So being able to travel backwards in time requires that there be a second temporal dimension, if only so that you can turn around.
(Visualizing a third temporal dimension would delve into the realm of the video I linked above.)
let me ask this – why would the universe appear differently with extra temporal dimensions? or would it appear different at all?
if there are multiple dimensions of time, we probably wouldn’t be able to notice it – our concept of time is so ingrained in causality it is neglected that our experience of time is inherently linear (subject to the physics governing our bodies) regardless of how our timeline may warp and bend (ie our characteristic line on the temporal dimensions will appear as a line to us always).
in fact we may already be dealing with more than one temporal direction…
recall that the amount of time passing for a relativistic clock compared to a stationary reference is T = t / sqrt(1 – (v/c)^2); T = proper time, t = time measured by relativistic clock. taking this as a ratio, you end up with: Q = / = sqrt(1 – (v/c)^2). i have arbitrarily called this ratio Q to simplify what follows… it is interesting to note that the form of this relation is identical to one you would find on a unit circle.
if you let V = v/c (again to simplify things), you can clearly see that V^2 + Q^2 = 1; in other words a locus form for a circle with rate of time as one axis and relative velocity as another (since Q is a function of all the components of a relative velocity vector, i could argue that it is still correct to state it this way).
either way. i prefer to compare the Q values of objects rather than our measure of time, since Q is provably frame-relative. proper time however is not dependent on the fame of reference, or at best refers to absolute time, or the time in an absolute reference frame. since we know from relativity that an absolute frame of reference cannot exist, it stands to reason that an absolute measure of time is impossible to assume. therefore Q seems more correct to use unless proper time and absolute time can be reconciled.
that being the case, that we cannot reconcile proper and absolute time without using an absolute frame of reference, we must then consider Q being a representation of some quality of the local space itself. that implies that Q will have a partial derivative with respect to position (GR) and with respect to velocity (SR). particularly in the case of change in Q relative to change in V, implies that Q is tied to acceleration more closely than velocity!
think about that for a moment – when you accelerate / decelerate, that is when your rate of time changes. this is a conclusion drawn from SR only, and yet in gravitation (GR) we find the same conclusion for completely different reasons – gravitation can be modeled on an accelerating frame of reference and gravitational time dilation is distinct to time dilation due to velocity / momentum (they can cancel eachother out such as for satellite orbits). what we must conclude is that the rate of time property Q is entirely dependent on relative acceleration and more profoundly, that it can work in the reverse – acceleration could be defined as the result of changing the rate of time, indeed some models of gravitation have shown that you can define gravity entirely by its effects on the flow of time.
if this is at all true, it would suggest that Q is at least an as-yet unexplored fundamental degree of freedom, therefore possibly a new dimension in and of itself. if that is true, it means there will be artifacts in the lorentz transform and measures of time and distance under extreme time dilation conditions.
this is all good and well in theory, but as it happens, the recent FTL neutrino incident seems to meet these conditions – we know the neutrino did not actually break the FTL barrier, but for all intents and purposes it was measured (and re-measured) to arrive earlier than the expected travel time for light (this is EXACTLY the measure used in the finding, travel time). such a contradiction of events, with all variables in the equipment and measurement technique ironed out to the best of our understanding of physics, would imply we are still not taking into account some information about what happened to those apparently FTL neutrinos – another dimension of time could explain this since it would explain the disagreement of the ‘length’ of a trip, by being a new component of that length measurement.
You know all those sci fi movies & TV shows where people travel through time. The films show time passing during the time travel–for example, Dr. Who has conversations with his guests, pulls levers, observes sparks flying out of his equipment. So if they are traveling THROUGH time, where (or when) is the time they spend inside their time machines? Gotta be a second time dimension–the time spent by a time traveller inside the time machine while it is traveling though time.
By the way, we are all already time travelers, traveling into the future at the rate of one second per second.
This is amazing. Even more amazing would be n-dimensional time.
Consider 3 different time dimensions. You’d be more than just everywhere at the same time. You’d be everywhere-everywhere, dispersing into everythingness.
Your everywhere would also be everywhere, your multiple places would also be in multiple places.
The only thing that I can think of to make an analogy or easy visualization of this is looking at a branching tree of possible realities.
I think it needs to be taken into account that we can not properly modify our movement in temporal dimensions, since they are heavily restricted:
It seems like we can only move forward on temporal dimensions and maybe change the speed with gravity a tiny little bit.
Doesn’t that make multiple temporal dimensions pretty pointless?
Imagine that concept with spatial dimensions:
Imagine a 3D world where the position on the Z axis is changing (nearly absolutely) equally for each particle with the “value” of Z growing (and never shrinking) with a constant rate.
Wouldn’t that essentially be a 2 dimensional world?
The movement on the Z axis, if it was measurable, could be used as time value even if they had a “proper time dimension”: For each state/value of the Z axis there is a unique state set of x/y values.
Or a three dimensional world where the y and z axis are behaving like the z axis in the previous example: It could only be inhabited by one dimensional beings.
The Y and Z axis could be seen as temporal dimension: For each value on them there is a unique state of the x axis.
I believe that’s how it is with multiple temporal dimensions:
They end up being completely inconsequential and we might as well have infinite temporal dimensions right now.
Does that make sense to anyone or does it sound like the confused rambling of someone who read too much scifi?
Perhaps it would be like seeing what happened around you in the past and in the future, but you also seeing the present at the same time.
Pingback: Dimensions | Science and rationality
Here’s one way to conceptualize an additional time dimension, orthogonal to our 3+1 spacetime dimensions:
Imagine the three spatial dimensions collapsed down to a single linear dimension, whose state evolves over time. The history of that linear world could be visualized as a 2D chart, with the state of the spatial line plotted at each point in time. With a second orthogonal time dimension, it would be possible for the entire history of that linear domain to itself evolve over the course of the second time dimension. This means that there wouldn’t be a single unique history of that world, but a continuously evolving history.
Let’s assume time progresses only forward in both temporal dimensions, and that such a world has three spatial dimensions, like ours. A denizen of that domain would then perceive the past not as a series of immutable prior events, but as a continuously mutating sequence of events whose history evolves over time. Every temporal point in the past would then have its own unique timeline extending into the future, not just the present moment.
This could provoke quite an existential crisis.
I believe that if we did live in a universe with 2 dimentions of time, that would basically mean we have multiple timelines. So turning a corner in time would probably be as simple as making a choice. (Or maybe 2 dimensions of time could create a universe that works like Dr. Who’s universe where time is non-linear, maybe even really allow for time travel.)
I think that only could exist two dimensions of time or time splitted with non orientable manifolds as mobius strips,but embbebedbin 6 dimensions of spacetime(4 space and two times)are two opposed orientations two,where that time would be as the particles and antiparticles could travel forward and backward in time,onde if transforming into other in the inversions of arrows of time.the f theory of superstrings appear indicate in that way in 12 dimensions with two dimension for the time
Not sure if this assumption is correct or not, but if the opposite of this universe existed, 1s x 3t, would it really be that different than our own? Couldn’t it be argued that in such a system, when you are would have a simmilar meaning as where you are in this universe, with where you are in the reversed universe being simmilar to when you are in this universe? Just a thought.
For the individual observer we are locked in step with one dimension of time and no degrees of freedom; we are unable to move backward or forward in time. That fact is not exactly true though thanks to Einstein. Apparently, we can travel to the future of some place we have been due to time dilation if only we could accelerate to an appreciable percent of the speed of light. Yet, we still cannot travel to our individual future since we ceased to live in that time when we set out on our journey. This suggests that there is another dimension of time, a 3+2, maybe 3+1 1/2 since other than proof of hypothetical curved time loops there doesn’t seem to be any way to travel to the past. We know we can look at the past of some other place, up to 13 billion + years, a kind of rotation in time, but not in real time. What a strange universe we live in.
It seems to me that the only reason we are having trouble with time being multidimensional is because we don’t like the idea that we aren’t masters of our own fate. If we have no free will and everything is predetermined then multidimensional time would not lead to causality paradoxes. If we turn around temporally, this thing causes that thing doesnt reverse. Everything just is.
One-dimensional time is like a dot moving along a straight line at a given speed, while two-dimensional time is like a dot moving across a piece of paper. Either way the dot moves at the same speed, and can’t go back. We still go forward, but in two dimensional time, we can go in different directions to each other, or to put it another way, move forward at different angles. Each dot may appear to the other to be moving through time at a different speed, but infact they are both travelling at the same speed, just at different angles.
Two dimensional time does not permit time travel any more than one dimensional time does, and certainly does not facilitate things that are in one object’s past moving to its future. You still can’t turn right around and go back the other way, any more than you can in one dimensional time.
Adrian’s point is near how my (undoubtedly incorrect beyond the limits of human comprehension to understand how incorrect) mental model of time works.
I view particle positions over time as filaments. E.g., I transpose time to a spatial dimension to mentally model it. And then, I remove one of the 3 spatial dimensions allow my 3D mental machinery to visualize it.
And what I get looks like a giant koosh ball, with the big bang in the middle and all the filaments (particle traces) emanating outwards away from the big bang, stationary since there’s now no temporal dimension. (Although, part of me wants to equate various quantum effects such as tunneling to an additional temporal dimension – vibrating the filiments… Which could lead to crazy things such as the history/present/future of the universe changing over the new temporal dimension – could we not only cease to exist but cease to have ever been? But I digress). Particle annihilation is when you view one filament as you travel outward from the big bang – you see two halves of the filament and then when they meet you’re at the end of the loop and they’re gone – same filament. Same for fluctuations that create particles, you’re just starting at the loop of a filament and then you view the two strands coming from the loop – the two “particles” are actually of the same filament.
In this view “time” movement is a measurement of any two filaments opportunity to interact, entwine, repel etc as they wind outwards away from the big bang.
So… for multiple time dimensions, instead of strands emanating from the big bang we have two dimensional planes in the case of one more temporal dimension. Just as our “view” of a particle at any point in time is a dot on the filament, it’s now a dot on a plane, somewhere along the flows of the two time dimensions.
Somewhere in my mind I want to ascribe as many temporal dimensions as there are physical constants to the universe with the “flow” of time on each temporal axis. And, the flow of “time” that we see in this universe to the flow of time as it tracks along the line where the physical constants are held constant. And thus, you could see a slightly different universe if you look at the “time flow” across slightly different versions of the universe’s physical constants. But, that’s just my human mental machinery looking for nice little explanations for things such as why we happen to live in a universe where the constants are handpicked to values that allow atoms, planets, life…. Eg it’s undoubtedly nowhere near reality.
Think about the quantum universe. What’s not forbidden is compulsory. You do all possible things at once, but the one you are observed to do is the one that you follow through with. This is similar to having multiple dimensions in time, like following three paths in a 2D time chart that all lead to the same place. It’s just a thought, and I don’t know how this would analogue to three or more dimensions. I’m not exactly an expert!
Pingback: Experiments Show The Effects of a Fourth Spatial Dimension?
This made me think of Larson’s Reciprocal Theory, which was supposedly a theory of everything. It is predicated on basic assumptions such as space being Euclidean, space and time being reciprocal, or s=1/t and t=1/s, with 3 spatial and 3 temporal dimensions. It was an interesting read, although I don’t remember too much about it. I think there was also something about the universe being one of motion, in that motion on or in the various dimensions of space and time give rise to different types of forces and phenomena. Which seems similar to some of what has been said above, which made me think of this. Regardless of whether it is true, it is an interesting thought. I mean it is easy to say, since we know there are 3 spatial dimensions, that there could be the same number of time dimensions. When I think of an extra dimension of time I hypothesize being able to completely disappear from one location in time and appear at another, essentially time travel. You would think that there would be either a completely different time-line existing alongside the one we know, or that one would be able to interact with our time-line in a new way, thus moving in a non-linear fashion.
I would think that, assuming you can only move forward in either time direction, time travel into the past would still not be possible, but I am using imagery to come to that conclusion:
I am imagining a time-area which is derived by combining two time-lines at a perpendicular angle. If you move forward on timeline 1, then rotate 90 degrees to timeline 2, change your position, then rotate back to timeline 1, it would appear you’ve instantaneously moved to someone who has remained on timeline 1. In my scenario, you would only be able to rotate 90 degrees to timeline 2, then 90 degrees back to timeline 1, so the restriction of time moving forward only would place restrictions on which direction you can rotate.
Admittedly, that is only a thought experiment of mine without looking into the actual physics models.
Pingback: 額外維度的真.物理 (The real physics about extra dimensions) | 論盡物理宇宙 – 某80後物理學博士的科普blog
“So, unfortunately, there are no actual answers to what the world would be like with more time dimensions, but (since it has nothing to do with reality) there’s no hurry to find those answers”.
https://phys.org/news/2007-05-two-time-universe-physicist-explores-dimension.html
I think Itzhak Bars might disagree about the relevance of 2D time to “reality”. Bars argues mathematically that our familiar world of four dimensions is merely a shadow of a richer six-dimensional reality. He describes the world as being like a two-dimensional wall displaying shadows of objects in a three-dimensional room.
He does a thorough reworking of the “people in a cave” idea, giving it a scientific and mathematical perspective that was previously lacking. Our accessible Universe becomes a shadow of something richer and more fundamental. However, the very fact that he is seriously working on this theory demonstrates the relevance and value of working within this “shadow”, acknowledging it as our “reality, and making full use of the laws of physics and mathematics that describe it.
Answer Gravy says: “But the laws we work with in physics just don’t extend in any useful way into higher dimensions without tacking on lots of weird extra restrictions that, in all but name, bring you back to a 3+1 dimensional universe”.
This must be so, because all these “laws” were derived in, and from observation of, our 3+1D Universe. Physicists cannot derive laws from something they are unable to observe; the best they can do is speculate; then devise the maths to test their speculations in hypothetical scenarios.
BTW, does anyone know if Bars is still working on this, and what, if any progress he has made? I can’t find anything more recent than 2007.
An extra temporal dimension would help explain 1) ufos appearing in our dimension then suddenly defying physics and gravity by traveling faster than reasonable speed to escape our atmosphere, 2) orbs of light / spooky lights suddenly appearing and the disappearing, 3) ghosts and supernatural incidents, 4) exponential increases in technological revolution. It all sounds science fiction, but really could be the intersection between two or multiple temporal dimensions. Our species is still so young. Physics is really just starting to be understood by the general population. In the past, only super intelligent people could theorize and share ideas with other super intelligent people. The internet has changed this. We should expect to live in a world with extra dimensions within the near future. I wouldn’t be surprised if some of us humans already had access to these dimensions. It’s fascinating.
Here’s a thought to explain entanglement…an extra dimension that has no time dimension. This extra dimension without time would exist everywhere at once and interconnect vast regions of space. The question then remains if this were a natural phenomena why wouldn’t we experience the anomaly which must result in its existence
. I postulate that the anomalous events have already taken place, with entanglement as just one aspect.