Physicist: We sometimes get questions about physical constants changing, and those questions make sense because there’s no real reason for the constants to be what they are. But π is mathematically derivable; it kinda needs to be what it is. You can’t, through the power of reason alone, figure out what the gravitational constant or the speed of light are, but you can figure out what π is.
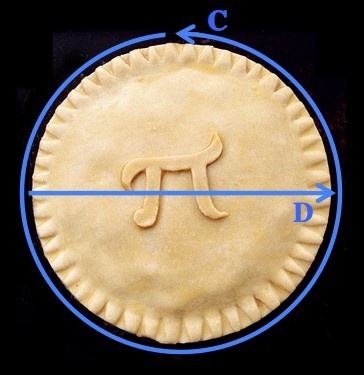
π is the distance around any circle, C, divided by the distance across that circle, D. All of the weird places that π shows up track back to this definition.
So this question is doubly profound! Unlike other constants, if π were different, then scientists (mathematicians especially) would continually have the sneaking suspicion that there’s something deeply, deeply wrong with the universe.
The definition of π seems pretty innocent (the ratio of the circumference of a circle to its diameter), but it shows up over and over in the middle of calculations from all over the place. For example, even though doesn’t, on the surface of it, have anything to do with circles, it’s still equal to π (there’s a loop floating around halfway through the calculation). A surprising number of calculations and derivations involve “running in a loop”, so π shows up all the time in electromagnetism, complex numbers, quantum mechanics, Fourier analysis, all over. In fact, in that last two, π plays a pivotal role in the derivation of the uncertainty principle. In a very hand-wavy way, if π were bigger, then the universe would be more certain.
Aside from leading almost immediately to a whole mess of mathematical contradictions and paradoxes, if π were different it would change the results of a tremendous number of (one could argue: all) calculations, and the fundamental forces and constants of the universe would increase or decrease by varying amounts. π shows up in way too many places to make a meaningful statement about the impact on the universe, one way or another.
Mathematician: The idea of giving π a new value of could be interpreted in a few different ways. For example:
1. That circular physical objects, as you make them progressively closer to perfect circles, approach a circumference to diameter ratio of something other than 3.14159… If this were the case, it might indicate something about the geometry of spacetime. If space is not flat, that can change geometric relationships. For instance, imagine drawing a circle on the surface of an orange. If we allow distances to be measured only along the orange’s surface (disallowing paths that penetrate the orange or go into the empty space around it), then the ratio of the circle’s circumference to diameter is no longer going to be π. It will, in fact, depend on the size of the orange itself. If our universe is not flat, but a curved surface, that could distort the geometric relationships that we measure on physical objects resembling circles.
2. That we change what we mean when we say π. Of course, π is just a symbol referencing an idea, so if the underlying idea that it references were to change, that would change the value of the symbol. But this is an extremely boring way to answer this question, reducing it merely to the redefinition of a symbol.
3. That we change which mathematical axioms we use. Most people think of math as a single, coherent set of rules. But when you get down to it, there are different possible sets of axioms that you can use to define mathematical concepts. By switching axioms it becomes possible to prove different things. If we were to choose a set of inconsistent axioms (i.e. axioms that lead to contradictions) then it would be possible to use this system to “prove” any mathematical statement true. In that case, you could show that π = your phone number, if you wanted.
If, on the other hand, you choose a set of axioms that are consistent with each other, but different than our standard math, you have to be more precise about what you mean by π. Usually, it makes no difference whether we define π to be the ratio of a circle’s circumference to its diameter, or whether we define it as
or
or
.
But when you start messing with axioms, it is going to affect what is provable, and therefore you have to be careful to specify precisely which definition you are using for π, since definitions that normally are equivalent using standard sets of axioms may no longer be. For some sets of axioms, there won’t even exist a mathematical entity that you reasonably could identify as being π.
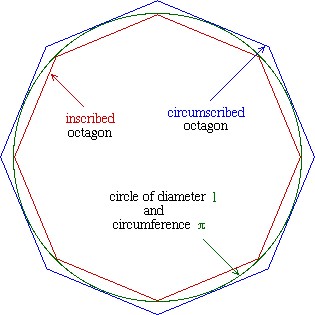
Answer Gravy: There are a couple of ways to derive the value of π. Archimedes estimated it by sandwiching the circle between regular polygons that he could find the exact sizes of.
However, we can use methods younger than a few millennia to derive cute formulae for π.
Coming from another angle:
So,
Since arctan(0) = 0, if you plug in zero you find that C1 = C2, so you can get rid of them and . Now,
, so
. Therefore,
. That
is based on the definition of the radian, which tracks back to the circumference of the unit circle being 2π, but the fact remains:
and changing the value of π means, among other things, that this summation would need to somehow equal something different. But it is what it is.







It’s too bad the question wasn’t pi=4, or you could just say we live in a universe where the overruling distance metric was taxicab rather than Euclidean 😀
Actually, is there a distance metric under which pi=3? If so, you could interpret the question that way.
I really wish there was, because that would tie up the question nicely. However, the amount that the ratio of the circumference, C, to the diameter, D, deviates from pi is, in some sense, a measure of the amount of curvature inside of the circle. For a tiny circle on the surface of the Earth, C/D ≈ π. For a “great circle”, like the equator, C/D = 2.
The only way I can see to make it so that increasing the size of a circle doesn’t change C/D, is to either use a flat space (in which case C/D = π) or have a flat space with a single point of infinite curvature. A more succinct term for this is “a cone”: the surface is flat, but the tip is infinitely curved. Any circle centered at the tip will have a constant C/D different from π, regardless of size. However, any circle that doesn’t contain the tip will have C/D = π, and any circle containing the tip, but not centered on it, won’t be a circle at all (it’s all weird and dented).
Point is, there’s no space with a constant value of C/D for all circles everywhere, other than flat space.
During the pi series derivation in the answer gravy, you incorrectly stated tan(1)=pi/4 whereas you should have put arctan(1)=pi/4. Just a simple typo, but besides that, great article!
Terry Pratchett has his own take on what would happen if you could create a circle where Pi = 3 😛
http://discworld.wikia.com/wiki/Bloody_Stupid_Johnson#The_Post_Office_Mail_Sorter
Thank you!
Oh I think you slightly misinterpreted my question/comment. You’re right about the value of π based on curvature, but you’re still sticking with the Euclidean distance metric in all those situations. I mean a different distance metric in that a different way of measuring distance between points.
Take the Taxicab metric then, where the distance between (x1,y1) and (x2,y2) is just (x2-x1)+(y2-y1). If you define a circle (in R^2) as “the set of points equidistant to a given point”, and you define π as “The ratio of a circle’s circumference to its diameter”, then under this distance metric the value of π is 4, and that is constant for any size circle. (It can be easily shown that a circle in this distance metric is a square rotated 45 degrees and centered at your chosen point. Take then a circle in this metric with radius r, and so diameter 2r. Then the length of a single side is 2r (each is up r and over r), so the length of the entire circumference is 8r, and so π=4.)
I’ve heard from an undergraduate professor that it was proven that, given this definition of circle and this definition of π, under any metric that satisfies the metric axioms, 3<=π<=4, but he couldn't find the article that proved it, and I've never seen it since, so I'm not sure if that's true or not.
It is important to remember that different distance metrics are purely mathematical constructions; actually applying a non-Euclidian distance metric to the universe would be just as complicated as applying a value of 3 to Pi 😛
Using non-euclidian geometry doesn’t actually make the question any easier to answer, it just rephrases the question.
To be fair, they aren’t necessarily a purely mathematical construction. It’s called the taxicab metric for a reason, after all; if you’re in a large city and someone asks you how to get to such-and-such building nearby where you are, you’ll probably answer “X blocks up and Y blocks over” or something of that nature. And if someone asked you how far away that building is, you’d probably say X+Y blocks rather than sqrt(X^2+Y^2) blocks. There’s some situations where we naturally use an alternate distance metric just because it’s more convenient to describe things that way. 😀
(Granted, I can’t think of any other real-life situation where a person would use an alternate distance metric, but it’s something, at least. 😛 )
When you hover your cursor over the pie, the caption reads pi(e). I would like to point out that pi(e) is my favorite number, and it is approximately 8.5397.
Love Long and Prosper
Took me a second Loctus but that funny of you =P. But these constants show up a lot in almost every sort of math. I have known of pi since I was a wee little kid but the real question is why do we always run into them?
Suppose you use taxicab metric on a triangular grid city (rather than square). Then a circle looks like a hexagon and pi = 3.
Maybe this is cheating by going to 1D, but on a number line, pi=2, since a “circle” radius r centered at the origin is just the points r, -r, and the circumference is 4r.
By using a 2D metric such as d((x1,y1),(x2,y2)) = min(|x2-x1|,|y2-y1|), you get pi=infinity.
You can get all sorts of weird values for pi.
That’s not a metric Ken; d((0,0),(0,1)) = 0 and (0,0) doesn’t equal (0,1). So still no examples where Pi is outside of [3,4].
What about pi for a circle rotating at relativistic speed?
If our universe were curved in such a way that pi equalled 3 or 4, wouldn’t we perceive that universe to be flat and this one to be curved?
I suppose that it would still be impossible to square the circle, so the area of a circle with integer radius would be rational, while that of a square with integer sides would be irrational. The entire meaning of multiplication would thus have to change, and we could no longer talk about 8 sets of 8 being 64 and so forth… So I guess this place wouldn’t work, because you wouldn’t be able to have numbered sets of indivisible objects… Unless the concept of quantity itself was fundamentally different.
What might work is altpi = 2pi, so when you turn completely around you are facing a different direction than if you don’t move or turn completely around again. At least your first face would be. Your second face would be where your first face started… If you rotated around your outstretched hand, it would be rotating with you so you’d see the same side(s), but if you rotated around a mulberry bush you would change which of your two faces was facing which side of the mulberry bush.
The only problem I see with that is that each indivdual particle would have one face each in rotationiverse 1 & 2, so in fact your face in 1 would have to be made of the same particles as in 2. You could get around this conundrum by making the different faces of the particles have different properties, so it would actually matter which face was facing where, because only one of the faces can see while the other shoots lasers from its eyes.
It wouldn’t still be impossible to square the circle, because the reason it’s impossible to square the circle is that pi is transcendental, and so it can’t be the solution to any polynomial with rational coefficients. The square root of any transcendental number is also transcendental, and squaring the circle would require a length that is a rational multiple of the square root of pi. However, a compass and straight-edge can only construct lengths that are solutions to polynomials with coefficients over the field of rationals with minimal degree some power of two (since you can take repeated square roots through constructing squares with diagonal equal to a given length). As a side note, the proofs of impossibilities of the other two classic Greek problems are similar; doubling the cube requires being able to construct a length of cubert(2), which has minimal degree 3 over the rationals, while trisecting an arbitrary angle also requires constructing a length with minimal degree 3 over the rationals by the triple-angle identity.
If pi weren’t transcendental, then that proof would no longer apply, and squaring the circle would be simple.
Hi ,
Pi(0)=4 seems a reasonable starting point for flat space . 4-x^27 =pi gives x= 0.99476
Space seems to be much more curved because of the limitation to 27 dimensions . You can derive the rest yourself .
Pi = 3. The Universe is a cylinder.
I can think that, only at the “beginning”, pi=3, then the universe was 2 dimensions only. After that, I have a curved development of the space, and the 3 dimensions result. If the Plank Time is true, and I have been able to measure how the universe was expanding from “t=0”, at every Plank time interval, I’d have a “decimal” of pi from the beginning, to the moment that I’m writing this comment…..
In other words, the simple Circle’s Circumference as a no infinite irrational number value, is perfectly defined in a “point” of the time. Pi, never has end in its decimal values, and it show how is the curvature of the space at every moment.
Spot on Mario, I agree.
The curvature of space time is inflating. If we could measure Pi in real time for a real circle to enough decimal places it would be constantly updating.
Hi Brian, and may be every decimal would be a number that mean how the space-time expansion is “working” at every instant. Why it isn’t a constant?, I don’t know.
We would need create mathematical formation about this assumptions.
Regards.
pi is 3 1/7 for a reason. In the beginning Pure time spacialized into 3.00 dimensions and 1/7 chronological time. The universe as it ages 6/7 of it’s lifespan adds to this original amount and becomes a 4.00 (New Jerusalem construct in the book of the revelations). Why so many people make it more complex than this?
At the end of one of Fred Saberhagen’s Berserker stories, one of the main characters receives a ring from a super-advanced race which, when you divided the circumference by the radius, yielded 3 rather than pi.
Wait, Mr. Physicist, didn’t Einstein reason the speed of light without measurement? In fact yes he did. Just because you can’t give something a value without measurement doesn’t mean you can’t use it as a constant-variable mathematically to both prove statements or know the values of other known measurements.
It is Einstein’s equations that have lead to the greater accuracy (in part) to knowing the “speed of light” because we can measure something else other than light, time.
This is equivalent to your claim that Pi can be reasoned but only in so much as another measurement is known, r = radius, even if that radius’ number were unknown we would still be able to reason that Pi(r^2)=area of a circle. or 2Pi(r)=circumference and etc. We could mathematically prove that the same way Einstein mathematically proved the speed of light.
To Gregory who claims Pi is 3 and 1/7 (best approximation). I am also Christian and I admire your attempt to tie mathematics to Jewish Mysticism but Sacred Geometry is far more advanced and 1/7 is a repeating “rational” number which is highly prized in Sacred Geometry.
I highly doubt such a number could also be approximated to suggest Pi will some day equal 4. It’s just not logical….
I don’t think sacred Geometry had enough information anyway, mathematics seeks God, therefore is Christian if used correctly.
But the ancient geometers never quite got to calculus let alone our current state of Mathematics.
@IDNeon: “Wait, Mr. Physicist, didn’t Einstein reason the speed of light without measurement? In fact yes he did.” Actually people had been measuring the speed of light for about 60 years before Einstein’s work on relativity, ever since Hippolyte Fizeau and Léon Foucault created their mirror apparatus. In fact, the entire reason he started his work in relativity was because of Michelson and Morley’s work in measuring the speed of light in 1887.
@IDNeon:
“But the ancient geometers never quite got to calculus, let alone out current state in mathematics.”
Actually, wrong. Scholars have found a big number of very ancient writings from civilizations as old as 3500 BC that contain very advanced calculus.
Actual calculus? As in, generalized methods of calculating derivatives and integrals? Do you have specific examples?
Ok, I am facinated by this conversation. I came here having been considering the value of pi for some weeks. It was troubling me that pi was not a rational number. I read a si fi book years ago , I think written by Heinlin, the story of which was set in a long cylindricle space station / space home with a diameter of several miles rotating to produce the effect of a gravity. The cylinder had farms, false sun light, and everything to sustain life for the duration of a long generational space journey, to find a new planetary home, light years away. The problem I foresore was the look on the welders face and the expletives of bugger, bugger, bugger! as he strugled to weld the seem of the cylinder because at a radius of some miles the edeges would not quite meet. if you see what I mean?
I also started to wonder if the issue had something to do with space time and the question of “life the universe and everything” So I was thrilled that space time was mention in this blog earlier. The consideration that space is not flat, ie the circle drawn on the orange is very interesting.
If pi is involved in so many important calculations does it mean that the relativity theory could have flaws or say that time travel might be possible because of the existance of an irrational pi?
You may have gathered by now that I am not a mathamatician. I left formal education with no math qualifications. I could follow examples off the black board to a point but left to solve the same problem with the values changed threw me most of the time. However, before computer software developed for my industry (I make windows door and conservatories) I did at least realise that I needed to use pythagoros to calculate angles and became self tought from a text book to achieve what I required. That said I do feel that I see problems in my minds eye as 3 diamentional so to speak and although I can’t come close to expressing the maths, I feel I have a sence for the questions to ask. I am quite pleased that the pi question has occured to many many other people and so I don’t feel that my thoughts are from an insane mind!!
Hi, I’m Willy. I’m a flatworm. I did not know pi was 3.14-something… nor that it was irrational. I don’t even know what “irrational” means. I’m just a flatworm.
My friend Riemann explained what pi is… He said it’s the ratio of the circumference of a circle to its radius. Ok… So I decided to make a big circle. I traveled in a straight line for one whole day and then took a left turn… I then continued along this path, always staying one day’s travel distance from my starting point the whole time. So I think I must have traveled along a circle. It took me exactly four days to return to the point where I started the circle. So I think pi must equal 4. Did I do something wrong?
Riemann says my value of pi must be different because I live on a sphere… but I wouldn’t know anything about that…
If we can devise measurements of different kinds by geometric methods, why not also with the transcendental ratio (Pi) of the circumference to the circle? For instance, we have a plank measuring 39.5″ and find we cannot divide it into three equal parts without obtaining a 13.66666 instead of a even number. However, if we construct a figure with an ascending arm into which we make an even division of three parts, then drop these parallel segments onto the board below, the 39.5″ board then becomes evenly divided (as proved by a Euclidean axiom). Could we not, then, slice up the remainder of that transcendental ratio into something “even” (rational) using such geometric constructs? Man is the measure of all things. Devise a new system of measurement as we did with our 39.5″ plank.
The problem is fascinating,.
If a circle of diameter d had one side sliced off (like a flat tire) such that the resulting perimeter was 3d, how long would that flat side be?
@The Physicist…
Really enjoyed the article and it gave me some things to think about. I doubt I’ll ever be doing much work beyond the 4th dimension or beneath the 2nd, so I’m not horribly worried about the effects of warped space-time on pi… but it’s nice to know some folks can conceptualize such things =D
@Robert…
Initially I thought the answer would be simple… but it seems my geometry skills are insufficient. I’m inclined to believe you have not provided enough information to give a definitive answer.
Depending on how accurate an answer you can accept, using some deductive reasoning reveals a shockingly close approximation. Since it doesn’t matter what d is, I assumed it to be a value of 1 and leverage it to work in my favor.
Let d represent the diameter
Let a represent the arc length
Let c represent the chord length
Let p represent the perimeter
Let R represent the radius of the circle = d / 2
Let T represent the angle of the arc in question
Assume d = 1
Given: p = 3d = 3 * 1 = 3
p = c + a = 3
Reasoning here…
For a semi-circle with a diameter of 1, the arc length is equal to Pi. Since p < Pi, this tells me that c < 1 and a <= Pi – c, or <= Pi – 0.999… (but for convenience I'm going to call it 1).
So, a = 3.1416 – 1 = 2.1416. And that is an angle in radians, so A = 2.1416.
Chord length can be calculated from a known angle and radius! c = 2 * R * sin(A / 2)
With substitutions:
c = 2 * (d / 2) * sin(A / 2) = d * sin(A / 2) = 1 * sin(A / 2) = sin(A / 2) = sin(2.1416 / 2)
= sin(1.0708) = .8776
So, now we've got a reasoned guess a and a calculated guess c… 2.1416 + .8776. How does this compare to the p we need of 3? 3.0192 (a more accurate Pi does not improve this significantly).
If an answer of "the flat side is ~ 0.8776d" is sufficiently accurate to your needs… golden. The error is less than 1%, but… a bit of trial and error narrowed it to .8738d (accurate to 4 digits anyway, but still not exact… I think the only accurate representation will include Pi :p )
Honestly, would love if someone could provide a more accurate means of determining this. I could not dredge up any correlations that were helpful without some other given measure. Who knows, maybe I bungled it entirely. Not something I would have attempted to answer on a "help forum".
Thanks! This is more than close enough for my purposes.
I was wondering, since pi is a mathematical term, and not a physical one, it can’t be altered..is my theory correct?
I am not a mathematician and only in middle school, but I was just thinking.
And if somehow, pi could be altered, would human life even exist?
I think that pi must be as it is because it represents pure change, pure movement, and…going out on a limb here…that is the substance of the universe. We describe and measure our objectively-experienced universe using points and lines. We can’t do pure curves. Humans can’t draw them. Computers can’t draw them. That is because they, themselves, we, can’t directly see the unbroken wholeness of the cosmos, the single undivided thread, the perfect circle. Rather, we are constructed, and ourselves construct, along the edges of the horizon of the curve; where it vanishes from our perception, we call that a point. But pi, with its neverending irrationality, its purity of change, gives us the clue that, from a cosmic perspective, there are no point or lines. Just the great circle. But this is nor mathematics, but mysticism…unless you’re Nicholas of Cusa.
pi respects a two dimensional relationship. If you go three dimensional, you simply
can change pi by changing the angle relative to the radiuses, creating a cone. Go ahead
and find a mathametical formula to define it, if you want, but it’s just geometry. Pi simply works in our physical world, but only up to a point – just like Einsteins theories
work in the world we know -up to a point. Eventually, you travel through a variable space/ time world until you break-out altogether. Then pi ratios seem rather insignificant and limiting.
Is pi mathematically necessary for existence, as we understand it? If so why?
Does pi literally define the relationship between dimension 1 and dimension 2 in our particular universe? Does our universe stay “propped up” because the relationship between dimension 2 and dimension 3 also happens to be pi? Otherwise the universe collapses? Is the pi for time dimension 2, where the circle has collapsed to a single dimension, so out and back circumference is twice the diameter which is just out but not back?
“You can’t, through the power of reason alone, figure out what the gravitational constant or the speed of light are…”
…yet.
It helps if you have a clearer perspective of the entire ‘universe’. Pi represents a mathamatical constant, an assumed agreed upon aspect of the physical world we live in.
The physical world we live in has it’s own set of rules, so to speak, it’s own microclimate,
that may or may not represent all of the universal ‘laws’. The sun will rise every day. If you want to delve into theortical physics, though, you can arrive at different ways that things can work. Since they are outside of the world we know, they don’t have to follow those rules. So, the question “can pi be 3” isn’t the correct question. That question justs
confuses the human line of reasoning. A slightly better question would be “does pi have to be 3.14?” The answer could then be “yes, in this world we live in, but not necessarily in the totality of the universe” or something to that effect.
Therefore – The question of ‘can pi be a variable number?’ is more of a theoretical tool than an actual proof. Thats probably why the crop circle regarding that was placed there.
My imagination of pi=3 creates an unending fractal spiral and could represent a constant expansion of the universe that is imperceptible relative to the rest of the universe. However, I am also fine with it as 3.14159 etc. nothing in my world has to work out as a rational number
I like your openmindedness and creativity
Its been a long time, but my question about pi =3 is about a fractal spiral, as presented
By the crop circle in the uk.