Physicist: There’d definitely still be a horizon if the Earth were flat. It would be in almost exactly the same place, and look essentially identical. While the Earth isn’t flat, adherents to that theory are correct in that it’s nearly so, and if you’re standing on the surface of a round something the size of the Earth it’s difficult to tell the difference (in fact, mathematically you can make the argument that a flat Earth acts the same as an infinitely big Earth).
For someone around 5’6″ tall, if the Earth were perfectly flat the horizon would be about 0.04° higher. That’s about the width of a (mechanical) pencil lead held at arm’s length. Unless you have short arms, in which case you’ll need to shave down the lead a little.
Even if the Earth were perfectly flat and went on forever, the horizon would still be exactly level: 180° of sky and 180° of ground (instead of the paltry 179.92° of ground we have). The only difference between a finite flat Earth and an infinite flat Earth is that no matter how tall you are on an infinite flat Earth, the horizon always stays in the same place.
However, even though the horizon of an infinite and flat Earth might actually be in the same place, it wouldn’t appear to be. An infinite plane has an extremely simple gravitational field; uniform and exactly the same regardless of distance. Normally the higher you are the weaker the gravity, but for a flat Earth that isn’t the case.
As such, light, which drops only imperceptibly under Earth’s gravity, has an infinitely great distance over which to do its dropping. The effect would require tremendous distances (as in; interstellar distances), but if you’ve got an infinite plane, that kind of distance is cheap.
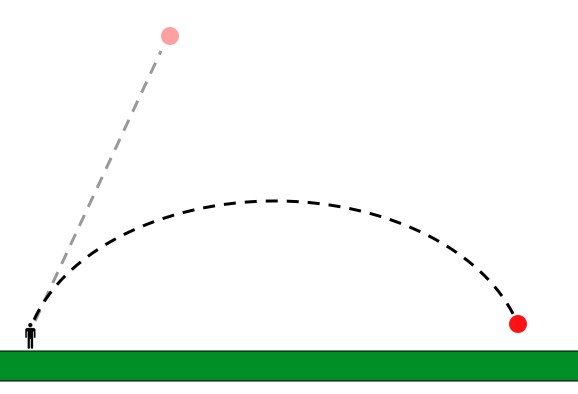
Given enough time and distance light will eventually curve back toward an infinite plane of matter. So if you’re standing somewhere on the surface and you look up you’ll see light that started somewhere else on the surface. Instead of a horizon, the world would look like it rises up on all sides and encloses you.
When you look up from what should be the horizon you’ll just see more of the infinite-flat-Earth. The one exception is what you’d see if you looked straight up. Directly above you you’d find the entire horizon bunched up at that point.
Answer gravy: It’s not interesting enough to include in the post directly, but here’s how the math above was done:
If you’re standing on a sphere with radius R and you’re H tall, then the distance from your head to the middle of the sphere is R+H. Your line of sight to the horizon is a tangent line to the sphere. This allows you to draw a right triangle and do a little trigonometry.
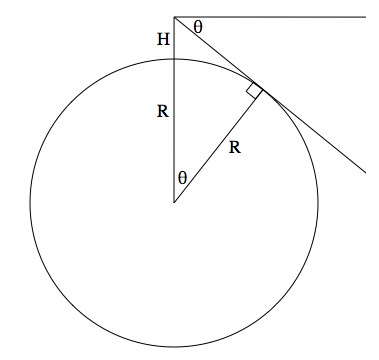
θ is the angle between the “true horizon” and the perfectly level “ideal horizon”. Coincidentally, it’s also the angle between where you’re standing on a sphere and the farthest thing you can see on the surface.
So, and
. Plug in R = 6,378,100 meters and H = 1.68 meters (which is 5’6″), and you find that θ = 0.04°.
By the end of college, electrical engineers and physicists get sick to death of the example of the infinite plane of anything (be it matter, electrical charge, kittens, whatnot). The reason an infinite plane is useful is that it has some nice symmetry. You can argue that, since no direction is special (by being close to an edge for example) gravity always points straight into or out of the plane-o-stuff. Symmetry is useful when you use a Gaussian surface, because you can ignore buckets of math.
Basically, draw a “bubble” around a lump of matter. The total gravitational field pointing through that bubble will be proportional to the amount of matter inside. So, the more matter, the more gravity. The bigger the bubble, the less the strength of the field through any particular part of the surface (by the by, there’s an example of this in action here). If the Gaussian surface you choose is a rectangular box that punches through the flat-Earth, then you find that it doesn’t matter how tall the box is.
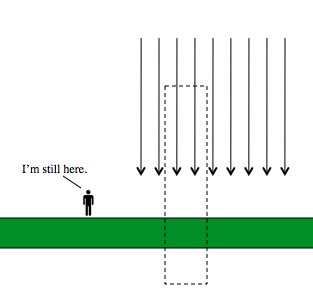
The total amount of gravity pointing into any imaginary box you can draw is always proportional to the amount of matter in that box. In this case, no gravity points through the sides (by symmetry) so it all points through the top. But if you make the box taller that doesn’t change. As a result, for an infinite plane gravity stays the same forever. QED y’all!
Uniform and infinite sheets of matter or charge have gravitational or electric fields that extend, without changing, forever. Of course, there are barely any infinite planes of stuff out there, so this isn’t a situation that ever actually comes up. However! If you’re close enough to a surface it can seem to be nearly infinite, so the infinite-plane solutions are often good enough.
And often as not, “good enough” is good enough for physics.








Wake up scientists, you have been programmed from the day you walked into your first class, books and universities, open your eyes for just a second, even to look at the evidence all around you, its in plane sight.
Professor Brian cox repeated the Einstein
Experiment using a cannonball and a feather
In a vacuum..Einsteins conclusion was
Simply this; both objects were in fact
STILL! Thus Gravity is an illusion! His
Curved space time theory it seems was
Born as a result..since the STILL objects
Were on a collision course with Earth.
So…unless the Ball Earth is constantly
Expanding in equal measures at approx
9.8m/s, it appears to be a flat plain
Accelerating in a vertical manner! Since
Both of these options are deemed
Outrageous, the curved space theory
Keeps the purists happy! Incidently.. He
(Einstein) admittedly failed in his optical
Experiments,to prove that it was the Earth
That moves!
That’s spins at up to 110mph! Obviously he
Must have initially thought about the collision
Between earth & the ‘objects’ & decided,
Hmm..better not go there!😁
Therefore, are we to conclude that since we can fly in one direction and end up at the exact same place on this planet (after flying “around” the flat Earth), that the edges of this flat circular plane connect (i.e. through something akin to an “Einstein-Rosen Bridge”) to corresponding coordinates at the exact opposite site of the circular plane, thereby creating the illusion one is circling a sphere?
No one has addressed what supposedly keeps the stops the Earth from becoming a sphere, gravity pulls everything to the centre of mass.
The thing i want to know is why i can see rottnest island while im having a swim 18.7 km away looking at the island with binoculars theres nothing over the horizon?
Also the rim velocity of the earth at the equator is 1000mph yeah? I wrap my head around the type of centrifugal force you’re looking at there by thinking of a skier getting whipped at the end of a ski rope at 50mph while the boat taking the short slower path turns round. How does water overcome this? How do we cling on gravity the amazing magical force that holds clouds to a 1000mph spinning ball traversing the sun at 17000 mph whilst we and all the planets shoot through space at 400000mph are you serious?. Wtf have scientists been doing?
If the suns 96 million miles away how come the varying temperatures all round the world at the same time
It really is up to you guys to sort this out. If we cant rely on science fact surely maths dont lie.
Something about the area of an equilateral triangle on a sphere
@Mars. Centrifugal force is based on rpm’s. At one rotation per day, that is not enough centrifugal force created to counteract the force of gravity. Based on the size of the earth, 1037 mph in rotation, is very slow.
You really need to clarify in this article that you are talking about the horizon – the place where the earth and sky meet.
In flat earth circles, this article is being used to “prove” that there would be an *obscuring* horizon even if the earth were flat with no gravity (flat earthers do not believe in gravity). There would be a horizon if the earth were a flat plane, yes, but it would not obscure objects beyond itself like the horizon on our spherical earth does. Also, the horizon would definitely not look the same for an observer at great altitude. Your opening statements do not specify that it would look the same to a viewer who is of average height. At a height of, say, 20,000 miles the horizon would not look the same over a flat earth!
Please add some clarifying remarks. Thanks!
1) The bulge in the earth is from centrifugal force due to rotation
2) This centrifugal force is obviously strong enough to buckle the earths crust, move millions of tons of water and actually squash down the whole planet
3) This force is not quite strong enough to have any effect on us Wait huh?
What is the exact mechanism that causes matter to attract matter from a far distance? Please provide specific steps in the mechanism.
Thank you,
“What is the exact mechanism that causes matter to attract matter….”
In classical mechanics we don’t know what the mechanism is, we just know that we can detect it and measure it.
I’m not sure whether the mechanism is fully understood in relativity or any of the other field theory, but since it’s 50+ years since I studied physics, I’m really not up with the play.
My main point, though, is that we don’t need to know the exact mechanism to know that it exists, that it is a different phenomenon from the other known forces of nature (strong and weak nuclear forces and electromagnetic force), though physicists would love to link them all together in a unified theory. Neither to we need to know the exact mechanism, to be able to measure it and use it to calculate all sorts of things from ballistic trajectories to time dilation. The fact that these calculations work out is a “proof of the pudding” proof of its existence.
Why are flatard morons infesting a site that deals in real science?
Hello,
Your analysis is right… for a planet without an atmosphere. An atmosphere blurs the horizon line, as you can see looking from an airplane window , so several thousands of air would definitely hide the geometric horizon under heavy haze. You included relativistic effects in your analysis, but again forgot about the atmospheric refraction , which would produce a ‘bowl’ effect long before we get into interstellar distances.
So, yes, there would be a (geometric) horizon, but not a definite, clear optical horizon as we see on our (spherical) Earth.
If the earth were flat, the horizon would look pretty much as it does now, until you neared the horizon. Then anyone, and I mean anyone, would develop a very acute case of acrophobia.
There would have to be some force in place that keeps the atmosphere, rivers, lakes, and oceans from leaking off the edge, unless they just slip over the edge and also exist on the Other Side.
If there is another side, then did life and evolution take place there?
Is the Other Side the source of UFOs?
If it is, what prevents the OtherSideians from tunneling through and having us for supper, so to speak?
Infinite is not possible because, in 24 hours, the Earth would sweep up everything in the universe, the Sun in 12 hours.
On a flat Earth, the horizon would rise up to the vanishing point of your eye-level.
Therefore, it would appear that you were standing in s shallow bowl, as deep as your eye height.
Jordi above is right, you – The Physicist – are wrong. If the Earth was flat, wo won’t see any clear, distinct horizon. It’ll all be hidden in a thick haze.
A gentleman agrees when is wrong, I expect you do the same and correct your answer.
I still think there would be an illusion that appeared as if you were standing in very large shallow bowl, because the angle between your eyes and the ground would decrease the further away you looked…
I love this comment section so much. I suppose it’s what happens when you bring up whether the Earth being flat or not. I mean, a guy who watches YouTube videos all day and is stuck in a constant echo chamber is obviously more knowledgeable than the entirety of accepted science. I am just so humored.
No matter how high our altitude, the horizon is always eye level. If you’ve ever flown in an airplane, and looked out the window, you would have seen this. This cannot happen on a globe earth. The earth is flat and infinite.
Liar.
You can see the horizon drop using a cheap 10 bucks theodolite app. You can also see quite clear curvature from 37000 feet and above.
Why do you lie in the internet?
You can see the curvature of the Earth standing on the beach on a clear day… No need to go to high altitude!
Indeed, the longitudinal curvature, you are right, of course.