Physicist: Almost every imaginable signal can be broken down into a combination of simple waves. This fact is the central philosophy behind Fourier transforms (Fourier was very French, so his name is pronounced a little wonky: “4 E yay”).
A complicated signal can be broken down into simple waves. This break down, and how much of each wave is needed, is the Fourier Transform.
Fourier transforms (FT) take a signal and express it in terms of the frequencies of the waves that make up that signal. Sound is probably the easiest thing to think about when talking about Fourier transforms. If you could see sound, it would look like air molecules bouncing back and forth very quickly. But oddly enough, when you hear sound you’re not perceiving the air moving back and forth, instead you experience sound in terms of its frequencies. For example, when somebody plays middle C on a piano, you don’t feel your ear being buffeted 261 times a second (the frequency of middle C), you just hear a single tone. The buffeting movement of the air is the signal, and the tone is the Fourier transform of that signal.
The layout of the keys of a piano (bottom) are like the Fourier transform of the sound the piano makes (top).
The Fourier transform of a sound wave is such a natural way to think about it, that it’s kinda difficult to think about it in any other way. When you imagine a sound or play an instrument it’s much easier to consider the tone of the sound than the actual movement of the air.
An example of a Fourier transform as seen on the front of a sound system.
In fact, when sound is recorded digitally the strength of the sound wave itself can be recorded (this is what a “.wav” file is), but more often these days the Fourier transform is recorded instead. At every moment a list of the strengths of the various frequencies is “written down” (like in the picture above). This is more or less what an mp3 is (with lots of other tricks). It’s not until a speaker has to physically play the sound that the FT is turned back into a regular sound signal.
Older analog recording techniques, like this vinyl record, record the original sound signal and not the FT.
In the form of an FT it’s easy to filter sound. For example, when you adjust the equalizer on your sound system, like when changing the bass or treble, what you’re really doing is telling the device to multiply the different frequencies by different amounts before sending the signal to the speakers. So when the base is turned up the lower frequencies get multiplied by a bigger value than the higher frequencies.
However, acoustics are just the simplest application of FT’s. An image is another kind of signal, but unlike sound an image is a “two dimensional” signal. A different kind of FT can be still found, and it is likewise two dimensional. When this was first done on computers it was found that, for pretty much any picture that isn’t random static, most of the FT is concentrated around the lower frequencies. In a nutshell, this is because most pictures don’t change quickly over small distances (something like “Where’s Waldo?” would be an exception), so the higher frequencies aren’t as important. This is the basic idea behind “.jpeg” encoding and compression (although there are other clever tricks involved).
An image and its Fourier transform. Notice that most of the FT is concentrated in the center (low frequencies). Deleting the FT away from the center saves a lot of data, and doesn’t do too much damage to the image. This is called a “low-pass filter”.
Interesting fun fact: the image of the woman in the hat is called “Lenna” and it’s one of the most commonly used standards in image-processing tests. It’s the top half of a adult image, and while it may seem strange that computer scientists would use that sort of image, the argument can be made that most comp-sci students don’t have too much experience finding any other kind.
While digital technology has ushered in an explosion of uses for Fourier transforms, it’s a long way from being the only use. In both math and physics you find that FT’s are floating around behind the scenes in freaking everything. Any time waves are involved in something (which is often), you can be sure that Fourier transforms won’t be far behind. It’s commonly easy to describe something with a single, simple wave, like pendulums or a single bouncing ball. Often (but certainly not always) it’s possible to break down complex systems into simple waves (or to approximately do this), then to look at how those waves behave individually, and then to reconstruct the behavior of the system as a whole. Basically, it’s easy to deal with “sin(x)” but difficult to deal with a completely unknown function “f(x)”.
Physicists jump between talking about functions and their Fourier transforms so often that they barely see the difference. For example, for not-terribly-obvious reasons, in quantum mechanics the Fourier transform of the position a particle (or anything really) is the momentum of that particle. Literally, when something has a lot of momentum and energy its wave has a high frequency, and waves back and forth a lot. Applying Fourier stuff to quantum mechanics is one of the most direct ways to derive the infamous Heisenberg Uncertainty principle! FT’s even show up in quantum computers, as described in this shoddily written article.
Mathematicians tend to be more excited by the abstract mathematical properties of Fourier transforms than by the more intuitive properties. A lot of problems that are difficult/nearly impossible to solve directly become easy after a Fourier transform. Mathematical operations on functions, like derivatives or convolutions, become much more manageable on the far side of a Fourier transform (although, more often, taking the FT just makes everything worse).
Answer gravy: Fourier transforms are of course profoundly mathematical. If you have a function, f, that repeats itself every 2π, then you can express it as a sum of sine and cosine waves like this: 
It turns out that those A’s and B’s are fairly easy to find. Sines and cosines have a property called “orthogonality”.
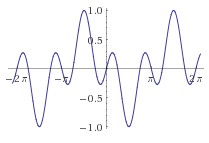
f(x) = sin(x)cos(2x). The orthogonality of sines and cosines is a statement about the fact that mixing sines and cosines of different frequencies creates functions that are positive exactly as often as they are negative (zero on average).
Now, say you want to find out what B3 is (for example). Just multiply both sides by cos(3x), and integrate from 0 to 2π.
![\begin{array}{ll}f(x)=\sum_{n=0}^\infty A_n\sin{(nx)}+B_n\cos{(nx)}\\\smallskip\Rightarrow f(x)\cos{(3x)}=\sum_{n=0}^\infty A_n\sin{(nx)}\cos{(3x)}+B_n\cos{(nx)}\cos{(3x)}\\\smallskip\Rightarrow \int_0^{2\pi}f(x)\cos{(3x)}dx=\int_0^{2\pi}\left[ \sum_{n=0}^\infty A_n\sin{(nx)}\cos{(3x)}+B_n\cos{(nx)}\cos{(3x)}\right]dx\\\smallskip =\sum_{n=0}^\infty A_n\int_0^{2\pi}\sin{(nx)}\cos{(3x)}dx+B_n\int_0^{2\pi}\cos{(nx)}\cos{(3x)}dx\\\smallskip = B_3\int_0^{2\pi}\cos{(3x)}\cos{(3x)}dx\\\smallskip = \pi B_3\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7Df%28x%29%3D%5Csum_%7Bn%3D0%7D%5E%5Cinfty+A_n%5Csin%7B%28nx%29%7D%2BB_n%5Ccos%7B%28nx%29%7D%5C%5C%5Csmallskip%5CRightarrow+f%28x%29%5Ccos%7B%283x%29%7D%3D%5Csum_%7Bn%3D0%7D%5E%5Cinfty+A_n%5Csin%7B%28nx%29%7D%5Ccos%7B%283x%29%7D%2BB_n%5Ccos%7B%28nx%29%7D%5Ccos%7B%283x%29%7D%5C%5C%5Csmallskip%5CRightarrow+%5Cint_0%5E%7B2%5Cpi%7Df%28x%29%5Ccos%7B%283x%29%7Ddx%3D%5Cint_0%5E%7B2%5Cpi%7D%5Cleft%5B+%5Csum_%7Bn%3D0%7D%5E%5Cinfty+A_n%5Csin%7B%28nx%29%7D%5Ccos%7B%283x%29%7D%2BB_n%5Ccos%7B%28nx%29%7D%5Ccos%7B%283x%29%7D%5Cright%5Ddx%5C%5C%5Csmallskip+%3D%5Csum_%7Bn%3D0%7D%5E%5Cinfty+A_n%5Cint_0%5E%7B2%5Cpi%7D%5Csin%7B%28nx%29%7D%5Ccos%7B%283x%29%7Ddx%2BB_n%5Cint_0%5E%7B2%5Cpi%7D%5Ccos%7B%28nx%29%7D%5Ccos%7B%283x%29%7Ddx%5C%5C%5Csmallskip+%3D+B_3%5Cint_0%5E%7B2%5Cpi%7D%5Ccos%7B%283x%29%7D%5Ccos%7B%283x%29%7Ddx%5C%5C%5Csmallskip+%3D+%5Cpi+B_3%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}f(x)=\sum_{n=0}^\infty A_n\sin{(nx)}+B_n\cos{(nx)}\\\smallskip\Rightarrow f(x)\cos{(3x)}=\sum_{n=0}^\infty A_n\sin{(nx)}\cos{(3x)}+B_n\cos{(nx)}\cos{(3x)}\\\smallskip\Rightarrow \int_0^{2\pi}f(x)\cos{(3x)}dx=\int_0^{2\pi}\left[ \sum_{n=0}^\infty A_n\sin{(nx)}\cos{(3x)}+B_n\cos{(nx)}\cos{(3x)}\right]dx\\\smallskip =\sum_{n=0}^\infty A_n\int_0^{2\pi}\sin{(nx)}\cos{(3x)}dx+B_n\int_0^{2\pi}\cos{(nx)}\cos{(3x)}dx\\\smallskip = B_3\int_0^{2\pi}\cos{(3x)}\cos{(3x)}dx\\\smallskip = \pi B_3\end{array}")
You can do this for all of those A’s and B’s, so 
Taking advantage of Euler’s equation, eiθ = cos(θ) + i sin(θ), you can compress this into one equation: 
Now here’s a big part of why mathematicians love Fourier transforms so much that they want to have billions of their babies, naming them in turn, “baby sub naught, baby sub one, through baby sub n”.
If you’re looking at a differential equation, then you can solve many of them fairly quickly using FT’s. Derivatives become multiplication by a variable when passed through a FT. Here’s how:
![\begin{array}{ll}\int f^{\prime}(x)e^{-2\pi i n x} dx\\\smallskip =-\int f(x)\frac{d}{dx}\left[e^{-2\pi i n x}\right] dx + f(x)e^{-2\pi i n x}|_{-\infty}^{\infty}\\\smallskip =-\int f(x)\frac{d}{dx}\left[e^{-2\pi i n x}\right] dx\\\smallskip =-\int f(x)(-2\pi i n)\left[e^{-2\pi i n x}\right] dx\\\smallskip =2\pi i n\int f(x) e^{-2\pi i n x}dx\\\smallskip =2\pi in \hat{f}(n)\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Cint+f%5E%7B%5Cprime%7D%28x%29e%5E%7B-2%5Cpi+i+n+x%7D+dx%5C%5C%5Csmallskip+%3D-%5Cint+f%28x%29%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5Be%5E%7B-2%5Cpi+i+n+x%7D%5Cright%5D+dx+%2B+f%28x%29e%5E%7B-2%5Cpi+i+n+x%7D%7C_%7B-%5Cinfty%7D%5E%7B%5Cinfty%7D%5C%5C%5Csmallskip+%3D-%5Cint+f%28x%29%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft%5Be%5E%7B-2%5Cpi+i+n+x%7D%5Cright%5D+dx%5C%5C%5Csmallskip+%3D-%5Cint+f%28x%29%28-2%5Cpi+i+n%29%5Cleft%5Be%5E%7B-2%5Cpi+i+n+x%7D%5Cright%5D+dx%5C%5C%5Csmallskip+%3D2%5Cpi+i+n%5Cint+f%28x%29+e%5E%7B-2%5Cpi+i+n+x%7Ddx%5C%5C%5Csmallskip+%3D2%5Cpi+in+%5Chat%7Bf%7D%28n%29%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}\int f^{\prime}(x)e^{-2\pi i n x} dx\\\smallskip =-\int f(x)\frac{d}{dx}\left[e^{-2\pi i n x}\right] dx + f(x)e^{-2\pi i n x}|_{-\infty}^{\infty}\\\smallskip =-\int f(x)\frac{d}{dx}\left[e^{-2\pi i n x}\right] dx\\\smallskip =-\int f(x)(-2\pi i n)\left[e^{-2\pi i n x}\right] dx\\\smallskip =2\pi i n\int f(x) e^{-2\pi i n x}dx\\\smallskip =2\pi in \hat{f}(n)\end{array}")
Suddenly, your differential equation becomes a polynomial! This may seem a bit terse, but to cover Fourier transforms with any kind of generality is a losing battle: it’s a huge subject with endless applications, many of which are pretty complicated. Math’s a big field after all.
The record groove picture is from here.
The Lenna pictures are from here.
The top picture with the four scientists is from here.
WAVE files usually store audio in pulse-code modulation (PCM), which is NOT a Fourier-transform based data, like you mentioned in the article. It’s just a bunch of samples, which are pretty much a discrete approximation of the raw waveform at that instant in time.
Mp3, on the other hand, does store frequency data, which is why it can throw away some frequencies that won’t matter to our limited perception, thus compressing the audio.
Just a minor correction, most WAV files use PCM, which basically records the amplitude of the sound wave at each point in time.
http://en.wikipedia.org/wiki/Linear_pulse-code_modulation
Waldo is basically straight up from the center of the picture. See the guy with the green shirt and red pants? Look just to his left.
Good stuff, Physicist. Thank you.
check out
http://search.wolfram.com/?query=fourier%20AND%20transform&collection=all&lang=en
specially the animated ones:
http://search.wolfram.com/?query=fourier%20AND%20transform%20AND%20animation&collection=all&lang=en
thanku sir………………..
thank you sir/madam…..good information..
Thanks for the article sir…
its really useful…
But a basic point is missing with me… i.e, theoretically FT will convert T-Domain to F-Domain … So, here my doubt is why to convert it…
PLEASE SIR REPLAY SOON … MY SEMINAR TOPIC CONTAINS IT…!!!
FT converts T domain to Frequency domain. I think, time domain and frequency domain are used as there for needed is his requirements. Just think about Low pass pass filter with time and frequency domain vice-versa.
good one. Iam thinking critically in terms of spectroscopic methods in chemistry such as ft- ir and ft-nmr
thanx 4 explaining in such a brilliant way..
Pingback: New mathematical techniques might allow for X-ray nanocrystallography | National Academy of Sciences
it’s very useful
i have doubt how can we say fourier transform will shows ones frequency spectrum
Laplace transform also does the same thing right?…T domain to F domain….where is the difference
A lot of problems that are difficult/nearly impossible to solve directly become easy after a Fourier transform. Mathematical operations on functions, like convolutions, become much more manageable on the far side of a Fourier transform.
I want to ask how FT used to solve the problems of convolution???
@raghad
The Convolution Theorem can be found here. The FT switches convolution with multiplication (which, as you say, is much easier to manage).
A very big thank to you.
what is z transform please reply it beause it seems that you will help me better.
thank you sir/mam.
Pingback: Q: Is there such a thing as half a derivative? | Ask a Mathematician / Ask a Physicist
laplace transform is a frequency domain representation of a continuous time signal.. whereas we use fourier transform can be represented in both was.. (continuos & discrete)
Pingback: Complex numbers and Fourier series
Fortunetely, I find the best website that I need. I get many knowledges from this.
Make the world better with Math and Physics.
wow
FT is used for non periodic signal. It converts time domain signal into frequecy domain. Mean it shows which frequency component are available into a signal.
Mostly used for filter designing…
how it is used for computer science people??
Hi
My doubt is regarding fourier series.. i understand that any signal (be it sine/cosine/square/triangle/or any other if exist) can be presented as summation of sine waves using the fourier series… in that case, the reverse is also possible – ie; by summing up appropriate set of sine waves, a particular wave type can be created with the help of fuorier concept.. if we present our ‘voice’ as a signal (which will appear a irregular,nonlinear signal) if plotted on a paper with time on x axis and amplitude of voice on y axis – can we not present this voice signal also by a series of sine waves ??? Theoretically,by removing a few sine waves or/and adding another few into this set, i could create the voice of someone else who is speaking the same sentence – am i correct with this concept – please guide me on my understanding.
thanks,
Rajith
Thanks for all replies .Can someone answer me,how to represent Fourier series by spherical coordinates???
This is quite a broad question and it indeed is quite hard to pinpoint why exactly Fourier transforms are important in signal processing. The simplest, hand waving answer one can provide is that it is an extremely powerful mathematical tool that allows you to view your signals in a different domain, inside which several difficult problems become very simple to analyze.
Its ubiquity in nearly every field of engineering and physical sciences, all for different reasons, makes it all the more harder to narrow down a reason. I hope that looking at some of its properties which led to its widespread adoption along with some practical examples and a dash of history might help one to understand its importance.
History:
To understand the importance of the Fourier transform, it is important to step back a little and appreciate the power of the Fourier series put forth by Joseph Fourier. In a nut-shell, any periodic function g(x)g(x) integrable on the domain D=[−π,π]D=[−π,π] can be written as an infinite sum of sines and cosines as
g(x)=∑k=−∞∞τkeȷkx
g(x)=∑k=−∞∞τkeȷkx
τk=12π∫Dg(x)e−ȷkx dx
τk=12π∫Dg(x)e−ȷkx dx
where eıθ=cos(θ)+ȷsin(θ)eıθ=cos(θ)+ȷsin(θ). This idea that a function could be broken down into its constituent frequencies (i.e., into sines and cosines of all frequencies) was a powerful one and forms the backbone of the Fourier transform.
The Fourier transform:
The Fourier transform can be viewed as an extension of the above Fourier series to non-periodic functions. For completeness and for clarity, I’ll define the Fourier transform here. If x(t)x(t) is a continuous, integrable signal, then its Fourier transform, X(f)X(f) is given by
X(f)=∫Rx(t)e−ȷ2πft dt,∀f∈R
X(f)=∫Rx(t)e−ȷ2πft dt,∀f∈R
and the inverse transform is given by
x(t)=∫RX(f)eȷ2πft df,∀t∈R
x(t)=∫RX(f)eȷ2πft df,∀t∈R
Importance in signal processing:
First and foremost, a Fourier transform of a signal tells you what frequencies are present in your signal and in what proportions.
Example: Have you ever noticed that each of your phone’s number buttons sounds different when you press during a call and that it sounds the same for every phone model? That’s because they’re each composed of two different sinusoids which can be used to uniquely identify the button. When you use your phone to punch in combinations to navigate a menu, the way that the other party knows what keys you pressed is by doing a Fourier transform of the input and looking at the frequencies present.
Apart from some very useful elementary properties which make the mathematics involved simple, some of the other reasons why it has such a widespread importance in signal processing are:
The magnitude square of the Fourier transform, |X(f)|2|X(f)|2 instantly tells us how much power the signal x(t)x(t) has at a particular frequency ff.
From Parseval’s theorem (more generally Plancherel’s theorem), we have
∫R|x(t)|2 dt=∫R|X(f)|2 df
∫R|x(t)|2 dt=∫R|X(f)|2 df
which means that the total energy in a signal across all time is equal to the total energy in the transform across all frequencies. Thus, the transform is energy preserving.
Convolutions in the time domain are equivalent to multiplications in the frequency domain, i.e., given two signals x(t)x(t) and y(t)y(t), then if
z(t)=x(t)⋆y(t)
z(t)=x(t)⋆y(t)
where ⋆⋆ denotes convolution, then the Fourier transform of z(t)z(t) is merely
Z(f)=X(f)⋅Y(f)
Z(f)=X(f)⋅Y(f)
For discrete signals, with the development of efficient FFT algorithms, almost always, it is faster to implement a convolution operation in the frequency domain than in the time domain.
Similar to the convolution operation, cross-correlations are also easily implemented in the frequency domain as Z(f)=X(f)∗Y(f)Z(f)=X(f)∗Y(f), where ∗∗ denotes complex conjugate.
By being able to split signals into their constituent frequencies, one can easily block out certain frequencies selectively by nullifying their contributions.
Example: If you’re a football (soccer) fan, you might’ve been annoyed at the constant drone of the vuvuzelas that pretty much drowned all the commentary during the 2010 world cup in South Africa. However, the vuvuzela has a constant pitch of ~235Hz which made it easy for broadcasters to implement a notch filter to cut-off the offending noise.[1]
A shifted (delayed) signal in the time domain manifests as a phase change in the frequency domain. While this falls under the elementary property category, this is a widely used property in practice, especially in imaging and tomography applications,
Example: When a wave travels through a heterogenous medium, it slows down and speeds up according to changes in the speed of wave propagation in the medium. So by observing a change in phase from what’s expected and what’s measured, one can infer the excess time delay which in turn tells you how much the wave speed has changed in the medium. This is of course, a very simplified layman explanation, but forms the basis for tomography.
Derivatives of signals (nth derivatives too) can be easily calculated(see 106) using Fourier transforms.
eȷωt
eȷωt
and complex exponentials are the eigenfunctions for linear, time invariant systems.
Put simply, if a system, HH is linear and time-invariant, then its response to a complex exponential will be a complex exponential of the same frequency but (possibly) different phase, ϕϕ, and amplitude, AA, — and the amplitude may be zero:
y=H[eȷωt]=Aeȷϕeȷωt
y=H[eȷωt]=Aeȷϕeȷωt
So the Fourier transform is a useful tool for analyzing linear, time-invariant systems.
Digital signal processing (DSP) vs. Analog signal processing (ASP)
The theory of Fourier transforms is applicable irrespective of whether the signal is continuous or discrete, as long as it is “nice” and absolutely integrable. So yes, ASP uses Fourier transforms as long as the signals satisfy this criterion. However, it is perhaps more common to talk about Laplace transforms, which is a generalized Fourier transform, in ASP. The Laplace transform is defined as
X(s)=∫∞0x(t)e−st dt,∀s∈C
X(s)=∫0∞x(t)e−st dt,∀s∈C
The advantage is that one is not necessarily confined to “nice signals” as in the Fourier transform, but the transform is valid only within a certain region of convergence. It is widely used in studying/analyzing/designing LC/RC/LCR circuits, which in turn are used in radios/electric guitars, wah-wah pedals, etc.
If the discrete time Fourier transform of x[n] is X(w) then what is the discrete time Fourier transform of x[-n+6]?
bad, not useful
what is the reason for amplitude get Half while converting Time domain to frequency Domain ………
Various dimension of real life signal in digital signal processing
Great post! Have nice day ! 🙂 rnwnf
Really I am Happy to get this web to read!
here we mention important aspects of Fourier transforms and discrete Fourier transforms as say prof dr mircea orasanu and prof horia orasanu specially in case of some differential equations and partial differential equations
also the Fourier transform can be used for other situations as heat and wave equations as say prof dr mircea orasanu and prof horia orasanu
I have a biological data, that repeats itself. how can we use Fourier transform and how it will be useful in extracting any information from that data
Hello Archana … if your data can be represented as sine or cosine waves or signals then you may use Fourier transform to enhance and extract data.
I believed that an FT IR spectrophotometer has improved signal to noise ratio because of the Fourier Transform?
Is that correct?
Archana, if you have a continuous time signal it can be represented as a discrete time signal, and with FT your DT signal will represent a sequence of identical samples. You will just need to extract a sequence to analyse your signal. It repeat itself every 2*Pi, and that will be sufficient. However, the frequency is analysed in rad/s instead of Hz, or can also be analysed with normalized frequency.