Physicist: A commenter from the original post was kind enough to point out a massively bone-headed mistake. My bad. In the calculation to figure out how long it would take the Sun to cool I had used Fourier’s law of thermal conduction. What I should have used was the Stefan–Boltzmann law of thermal radiation. So that calcu-estimation would have been perfectly valid if the Sun were floating in an expanse of very cold, and opaque, material and not valid if the Sun were floating in a whole lot of nothing. Sadly, the universe has taken effectively none of my constructive suggestions, and the Sun persists with being in space. After a revisit (included in the answer gravy below) it looks like we’d still have plenty of time to leave the planet, but longer time scale things would be done (continental drift, presidential campaigns, etc.). Life has existed on Earth for about 4 billion years, but interesting, multicellular life only exploded onto the scene about half a billion years ago. Assuming that this is because the Sun wasn’t doing it’s job at the time (the Sun gets brighter over time, and was dimmer in the past), that puts a floor of about 95% of its present output necessary for complex life. If fusion stopped, we’d be there in a little over a million years.
Science is based on the little-acknowledged axiom that not a single one of us is particularly smart, but that there’s a good chance that somebody out there is busy not making mistakes today (and who tomorrow may rely on you). To that end, what follows is a more direct calculation, for those of you interested in the details.
Answer Gravy:
The Stefan-Bolzman law says that the flow of heat out of the Sun should be 
Plugging this into the Stefan–Boltzmann law:
Fans of calculus can tell you that the solution of this is:
![\begin{array}{ll}\dot{T} = -\left(2\times 10^{-26}\right)T^4\\\Rightarrow \frac{dT}{dt} = -\left(2\times 10^{-26}\right)T^4\\\Rightarrow T^{-4}dT = -\left(2\times 10^{-26}\right)dt\\\Rightarrow -\frac{1}{3}T^{-3} = -\left(2\times 10^{-26}\right)t +k\\\Rightarrow T^{-3} = \left(6\times 10^{-26}\right)t +k\\\Rightarrow T = \left[\left(6\times 10^{-26}\right)t +k\right]^{-\frac{1}{3}}\end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D%5Cdot%7BT%7D+%3D+-%5Cleft%282%5Ctimes+10%5E%7B-26%7D%5Cright%29T%5E4%5C%5C%5CRightarrow+%5Cfrac%7BdT%7D%7Bdt%7D+%3D+-%5Cleft%282%5Ctimes+10%5E%7B-26%7D%5Cright%29T%5E4%5C%5C%5CRightarrow+T%5E%7B-4%7DdT+%3D+-%5Cleft%282%5Ctimes+10%5E%7B-26%7D%5Cright%29dt%5C%5C%5CRightarrow+-%5Cfrac%7B1%7D%7B3%7DT%5E%7B-3%7D+%3D+-%5Cleft%282%5Ctimes+10%5E%7B-26%7D%5Cright%29t+%2Bk%5C%5C%5CRightarrow+T%5E%7B-3%7D+%3D+%5Cleft%286%5Ctimes+10%5E%7B-26%7D%5Cright%29t+%2Bk%5C%5C%5CRightarrow+T+%3D+%5Cleft%5B%5Cleft%286%5Ctimes+10%5E%7B-26%7D%5Cright%29t+%2Bk%5Cright%5D%5E%7B-%5Cfrac%7B1%7D%7B3%7D%7D%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=0 "\begin{array}{ll}\dot{T} = -\left(2\times 10^{-26}\right)T^4\\\Rightarrow \frac{dT}{dt} = -\left(2\times 10^{-26}\right)T^4\\\Rightarrow T^{-4}dT = -\left(2\times 10^{-26}\right)dt\\\Rightarrow -\frac{1}{3}T^{-3} = -\left(2\times 10^{-26}\right)t +k\\\Rightarrow T^{-3} = \left(6\times 10^{-26}\right)t +k\\\Rightarrow T = \left[\left(6\times 10^{-26}\right)t +k\right]^{-\frac{1}{3}}\end{array}")
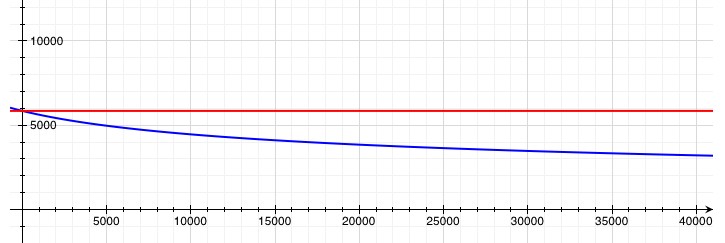
Here k is an “integration constant”, and it’s set so that the temperature right now (at t=0) is what it should be: 5878. Also, t is in seconds in σ. To fix that, just multiply t by 31,500,000,000 (the number of second in a thousand years) to change it to millennia.
The surface temperature in °K vs. time in thousands of years.
So all together, if fusion were to stop today, the Sun’s surface temperature should be about ![T = \left[\left(6.3\times 10^{-19}\right)t +5\times 10^{-12}\right]^{-\frac{1}{3}}](https://s0.wp.com/latex.php?latex=T+%3D+%5Cleft%5B%5Cleft%286.3%5Ctimes+10%5E%7B-19%7D%5Cright%29t+%2B5%5Ctimes+10%5E%7B-12%7D%5Cright%5D%5E%7B-%5Cfrac%7B1%7D%7B3%7D%7D&bg=ffffff&fg=000000&s=0 "T = \left[\left(6.3\times 10^{-19}\right)t +5\times 10^{-12}\right]^{-\frac{1}{3}}")
Hi
If the fusion stops, I heard that the star would start shrinking due to gravity.
so the volume is reduced. Is this effect considered in the equation? please let me know.
You’re right, and it definitely isn’t taken into account here. I ignored that effect by taking into account laziness, but for the first percent or two of temperature loss it shouldn’t be a big effect.
Is there any way to detect that fusion in the sun has stopped? IF it takes millions of years to notice could the effect occur without us knowing?
Pingback: Q: If fusion in the Sun suddenly stopped, what would happen? | Ask a Mathematician / Ask a Physicist
The original post mentioned this briefly. There are a handful of facilities around the world that can detect and study solar neutrinos, which are produced at a few points during the fusion process. Unlike regular matter and light, neutrinos almost never interact with matter, so they exit the Sun and are detected immediately.
And yes; the “barely interacts with matter” thing does make neutrinos hard to detect, but it can be done.
Call me a moron, but wouldn’t we lose the light produced in the approximately 8 minutes it takes for light to get from the now dead sun to the earth, and then we would be engulfed in darkness?
Nope!
The light we get from the Sun is “thermal radiation”, which is light created by virtue of the Sun being hot. The Sun shines as long as the Sun is hot.
Actually, I think the contraction of the sun would matter. The volume of the sun is (somewhat) linear with respect to temperature, right? That means that a small decrease in heat should release an amount of gravitational energy which is vaguely proportional to it, right? Doesn’t that effectively make the heat capacity larger?
would the shrinkage from gravity cause it to heat up (or at least slow the cooling)?
The effect of gravitational collapse is definitely significant (enough to change the answer you got by many orders of magnitude). And the primary reason for that is that as the sun collapses, gravitational potential energy is converted to heat.
For an illustration of how significant the energy from gravitational collapse is: The current gravitational binding energy of the sun is 6.9*10^41 J (i.e. if a very dilute gas cloud with the same mass and composition of the sun were to collapse into the current configuration of the sun, it would release 6.1*10^41 J of energy). And the sun is currently radiating 3.95×10^26W of power. Divide the two and you get roughly 50 million years.
The sun has been shining for about 5 billion years, so roughly 1% of the energy output by the sun so far came from the gravitational collapse of the gas cloud forming the sun, with the remaining 99% coming from nuclear fusion.
And since gravitational potential energy goes as -1/r, there is a LOT more gravitational potential energy available. The sun can keep collapsing until it becomes white-dwarf sized, at which point electron degeneracy pressure will stop the collapse.
Wouldn’t the effect be the same as the sun running out of “fuel” which it can fuse? I believe that is a normal stage in the evolution of stars and I would think the sun would turn into a white dwarf. See http://en.wikipedia.org/wiki/White_dwarf
The Sun will basically shrink, then grow and swallow the Earth in 6 months
Plus, the math proves it
Wouldn’t gravitational collapse from the lack of fusion generate a shockwave that would destroy the earth?