Physicist: If all you had access to was the remaining particle, you’d never know the difference.
The way entanglement is often described in popular media makes it sound like voodoo; there’s some kind of magical connection between two or more particles, and doing something to one instantly affects the other. From this point of view it might seem as though you could learn something about the inside of black holes by dropping entangled particles into them, or maybe the outside particle would start acting black-hole-ish.
In practice (reality), entangled particles don’t have any kind of connection with each other, they’re just correlated in a funny way. In quantum physics things can be in multiple states, such as being in multiple places or multiple energy levels. This is called a “superposition“. In classical physics things can only be in one state (I can’t tell you where my keys are, but they’re definitely not in more than one place).
So, say I’ve got some paper bags and one red and one blue marble. Classically, the marble is either red or blue, but not both. In quantum mechanics you could prepare a state that’s a superposition of red and blue.
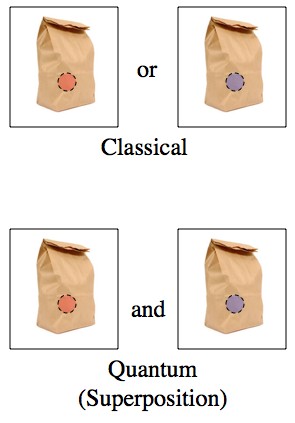
Top: the marble is definitely either red or blue.
Bottom: the marble can be in a superposition of red and blue.
Oddly enough, you can’t describe the world by describing the state of each particle individually. You have to include states that involve multiple particles that are in multiple states. Bringing a second bag into the picture, and putting one of the two marbles into each, we find that there are two possible states: red/blue and blue/red. In quantum mechanics, there’s no problem having a combination of these two states as well. Notice that since there’s only one marble of each color, the bags are correlated; if you know what’s in one, then you know what’s in the other.

Top: if one bag has a red marble, the other has a blue and vice versa.
Bottom: if one bag has a red marble, the other has a blue and vice versa. However, both bags have both red and blue. In the same way that a single particle can be in multiple states, the bags together are in the states “red/blue” and “blue/red”.
There’s more detail about what exactly entanglement is and how it behaves here, but suffice it to say, when things are correlated and in a superposition of states they’re entangled. So finally, with that background we can take a look at what happens when you destroy or just take away half of an entangled pair.
A black hole, in addition to all of its other weird properties, does a really good job doing exactly that. For all practical (experimental) purposes, dropping a particle into a black hole destroys it plenty. By watching the black hole afterward, it would be impossible to recover information about the one particle you dropped in. So, what you’re left with is a single particle that’s still in a superposition of states.

Destroying or sufficiently scrambling half of an entangled pair leaves a single particle in a not-entangled superposition.
This, by the way, is what you have even if you don’t destroy the other particle. Without access to both halfs of an entangled pair, there’s no way to determine if they’re entangled at all.
There was a big debate between some of physic’s heavyweights over whether or not things that fall into black holes are genuinely destroyed, including all of their information, or if information is somehow preserved. After a few decades of debate, the consensus today is: no, information is conserved. This has lead to some new ideas like black hole entropy, Hawking radiation, holography theory, and black hole computation (this last one is a little more far-fetched than the others). In theory, if you somehow managed to keep track of absolutely every detail of everything that fell into the black hole, and then managed to collect most of the Hawking radiation produced by the black hole over its entire life time (which is much, much greater than the age of the universe), then you could in theory have a pretty good chance of correctly guessing which “marble” fell in.
But, for all intents and purposes, if you have an entangled pair of particles and you drop one into a black hole, you’ll be left with one particle that is still technically entangled to the other, but it doesn’t matter. It’ll behave like any other particle.
Answer gravy: There are buckets more to be said about breaking entanglement, and the statistics of entangled pairs (and halfs of entangled pairs), including the exact nature of the superposition of the remaining particle. Way too many buckets to fit into one article. However! There’s a great resource that goes into ludicrous detail here. The stuff relevant to this post is in chapter 4.







Wait, I’m confused. How can the lifetime of the black hole be much greater than the age of the Universe?
That was poorly written on my part.
An run-of-the-mill black hole would take around 1069 years to completely evaporate, which is about 100,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 times older than the present age of the universe.
I’m confused as to how you can prove a superposition without a connection between two particles. I understand that they are not connected physically, but because they behave that way it makes no sense to me that they are separate or distinguishable from eachother…
It’s a little subtle. Basically, you prepare a huge number of particles identically, and then look at their statistics. This is how almost all of the great experiments in quantum physics are done.
Particles in a “pure state” behave in a very predictable way (or at least a measurement can be found in which they behave predictably), and particles in a “mixed state” are always at least a little random. In the case of a “maximally entangled pair” each particle, on its own, is in a mixed state and is completely random regardless of measurement, and yet taken together the two particles form a pure state. This is the subtlety I wanted to avoid in the post.
By the way, none of that should make any sense at all, so don’t stress. The last link in the post does talk about it in detail (although, looking at it again, it helps a lot to have read chapters 2 and 3 already, and to have a little back ground in quantum mech).
Whenever someone talks about Quantum Mechanics I always get a little wierded out because they keep saying that it shouldn’t make any sense at all but it makes plenty of sense to me once the terminology is explained and I’m pretty sure that means that I’ve operating on some kind of serious misconception.
As I understand it, I think this post is incorrect when it says that a particle in the superposition (|0> + |1>)/sqrt(2) is indistinguishable from having access to the first particle of the pair (|01> + |10>)/sqrt(2).
To see this, subject the first particle of the pair to the unitary transformation
|0> -> (|0> + |1>)/sqrt(2)
|1> -> (|0> – |1>)/sqrt(2)
If we have a particle that is not entangled, so it is described simply by (|0> + |1>)/sqrt(2) and we apply this transformation, we get the state |0>, so that we are certain to find 0 as the result of a measurement.
On the other hand, if our initial state is (|01> + |10>)/sqrt(2) and we apply the same transformation, our final state is
(|01> + |11> + |00> – |10>)/2
When we measure the first bit, we get 0 and 1 with equal probability. Thus, it is possible to determine whether the particle is entangled.
In fact, this entanglement is exactly what “making a measurement” means. Suppose we have a right a left slit in a double slit experiment. If we send some photons towards the slits, we might call going through the left slit 0 and the right slit 1. Then if we set it up right, the particle can have equal amplitudes for both slits and be in the state (|0> + |1>)/sqrt(2). Allowing the particle to be detected on a screen beyond the slits acts in much the same way as our example unitary transformation. We see interference on the screen, which is analogous to always measuring 0. However, if we have a detector at the slits that measure which slit the particle went through, that detector becomes entangled with the photon, and we now have the state |0L> + |1R>, where L and R represent the state of the detector when it knows the photon has gone through the left or right slit respectively. So long as the detector has perfect information – as long as L and R are orthogonal – we no longer see interference at the screen. This is how measurement destroy interference.
In regards to the previous comment by Mark Eichenlaub I would love to know the physicists response to his ideas about the collapse of the wave function in the double slit experiment and if it is in fact the particle entangling with the measuring device?
I know entanglement takes very specific situations to take place, but could this be an explanation for the collapse of the wave function?
It doesn’t make much sense though. If the detector is not there, then the photon can go through both slits and act like a wave. Once you put the detector there then the photon should still act the same, unless you have retrocausality taking place whereby the photon goes through both slits, is measured and then entangles itself with the detector and then goes back to acting like a wave. How can the photon KNOW to act differently?
There’s a post here that tries to talk about that a bunch.
outside a blackhole there is a region of no retunr i.e event horizon.if 2 particles so said ”tangled”(cuz particles can only be in interaction to one another at only one point) were having numerous paths available in space outside the event horizon they may move in any direction breaking thier contact but when either one of them crosses event horizon( where all the paths availabe in space will be directed towards centre of a blackhole )it will fall into it not necesserally ”tangled” due to reason given above.larger blackholes are deformations in spacetime ,cant evaporate.
Why not to assume that the entangled particles are actually physically connected (like 2 balls on either side of a stick)? in such case no info passes from ball A to Ball B (thus no violation of speed of light, causality, locality). When you move one ball the other moves the same due to the connecting ‘stick’ between them, not due to ass of info. The fact that at the moment you can not detect the ‘connecting stick does not mean that its not there
Inside Black Holes http://youtu.be/yMRYZMv0jRE?t=38m00s ; a equals rb theory
what if we throw an object with > or equal to speed of light ,opposite to rotation of earth then would the object travel to past or would no change occur
The Physicist, delving a bit into hypotheticals for a moment, if you wouldnt mind. There are theoretical uses for entanglement, for this question, long rang instant communication. Could you use a so called Q-phone(I had to make a pun somewhere, forgive me) to observe conditions on the opposite side of the event horizon? It would seem to me that if a particle is entangled, that position, or location of a particle should not affect its ability to ‘communicate’ with the other. As I understand black holes(which I may be woefully misinformed about) particles do not simply cease to exist past the event horizon. Is this incorrect? What do our theories say on this hypothetical situation? I understand that the idea itself may violate causality, but please, humor me. Am I incorrect in stating that position and forces do not influence the entanglement of a particle(assuming shielding from decoherence), in the sense that no classical force can disrupt it?
It might be that gravity cold be explains with some entanglement also..
Now we know about Highs and the gravity could be a phenomenon in that field… Than layers of universe and it is time for fuzzy logic
the force that’s between the entangled particles moves faster than light, can it escape the pull of a black hole? can we use that force to transmit data out of a black hole?
I don’t know if this is the right thread or even forum to ask this, so I hope you’ll bear with me and consider my question simply as an intellectual curiosity, as I very much enjoyed reading your posts, linked sources and feedback from the community.
I assume that several particles can be entangled? From what I could gather the answer was yes but correct me if wrong.
If so, and here’s the first question, could the phenomenon of consciousness have a root in a larger quantum structure, where certain substructures are shared widely among groups (plants, animals), narrowing down to different species and eventually to individual organisms?
What I have in mind is a sort of God, which we can call a quantum server for science sake, distributing common ‘software’ among clients through the phenomenon of quantum entanglement (ie laptops on a network, or humans/animals), that provides a common interface (happiness, sadness, anger) and the general building blocks for cognitive development. Then as each instance is used in different ways it evolves individually through its life cycle, not to mention biological influences (nature vs nurture).
Finally, asking from a physics perspective, is there any known quantum mechanism to provide feedback to that God (server) from the individual nodes (plants/animals) containing unique information from their individual experiences, influencing and changing that core information that was universally distributed, so that the accumulation evolves that distributed system over time, giving Darwin a kick up the ass?
In summary, could a massive structure of particles, containing some entangled particles, create new entanglement relations from non entangled particles that belong to that same structure and sub structure?
@Danny
I don’t really know, but that’d make a great science fiction story!
Talk 2 Bill Gates U all will controlled soon just look at the stylites that where sent into space just 2 control U don’t take the mark of the Beast 4 it’s here know trust me so u die it’s a much better place then hell
I was looking for a seemingly absurd hypothesis that stated that if an entangled electron was captured by a black hole, and the electron it is entangled with escapes and orbits the black hole once, the electron would see a copy of itself. If that same electron orbits the black hole twice, it would then an infinite number of copies of itself. It sounds so blatantly false that I was hoping to get feedback from this particular post and thread. Thanks in advance.