Physicist: Contrary to its exciting name, quantum teleportation doesn’t involve any physical stuff suddenly disappearing and then reappearing somewhere else. Instead it’s a cute, clever, technique for transferring an unknown quantum state of one system (usually a single particle) to another, specially prepared, system. That sounds a lot cooler and more interesting than the reality. Before even getting into quantum teleportation, I’ll describe how to do “classical teleportation”, and you can judge whether “teleport” is even the appropriate word. This is great at parties (or, more likely, Dr. Who marathons at your mom’s house)!
Classical teleportation:
i) Get three coins (hereafter called A, B , and C), and set up B and C to be the same side up (but which side is up should be completely random).
ii) Flip A.
iii) Compare A and B. If they’re the same, then leave C alone. If they’re different, then turn C over.
iv) What was the heads/tails state of A is now the state of C.
B and C start the same. If A and B are the same, then C and A are already the same. If A and B are different, then flipping C will make A and C the same. This works independently of the heads/tails configurations (as long as B and C start the same), so you don’t even need to know what faces are up.
What’s deeply spooky about this is that you can set it up so that the state of A is transmitted to C, without ever knowing what the states of any of the coins are. In step one make B and C the same, then while holding them together, turn them over several times until you’ve lost track of how many times you’ve done it, then cover them. They’ll be the same, but you won’t know which side they both have up. Do the same sort of thing in step three: bring A and B together, turn them over several times, then see if they’re the same or different.
Or just get someone else to do it for you.
The “teleportation” comes in because you can move C as far away as you like. Once you compare A and B you can then shout (or, for a long distance teleport, call on the phone) “same” or “different”, and whoever has C can leave it alone or flip it over. The unknown state of A has been teleported to C. Notice that, until you tell C’s owner about the result of the same/different measurement, the state of C has absolutely nothing to do with the state of A. This is the big limitation of teleportation and why it isn’t faster than light; you have to communicate the results of the measurement, and that communication is through ordinary, not-faster-than-light channels. Without that communication C remains random and has nothing to do with A.
Whether or not this trick qualifies as remarkable, or even deserves the moniker “teleportation”, is a matter of personal preference. That said, this brand of teleportation can send physical objects from place to place exactly as effectively as an email can.
Quantum teleportation is not this. Not this at all.
Quantum teleportation has the same limitations and works very similarly.
Answer gravy: And here’s how. There are several teleportation schemes and, believe it or not, this is the simplest.
The basic idea is the same as the coin trick; you start with two particles, B and C, that are entangled. Then you bring in particle A that’s in an unknown state and compare it to B (in a way that doesn’t involve directly measuring the states of either). Then the results of that comparison are communicated, and C is altered.
A “qubit“, is like a regular “bit” (or a coin), except that instead of just 0 or 1 (heads or tails) it can be in a combination of both. What is physically meant by 1 or 0, or how a qubit is manipulated, depend on the system involved. It could be electron spins manipulated by magnets, or photon paths manipulated by beam splitters, or a dozen other things. Doesn’t really matter.
The notation here is a little tricky, but stay with me. In what follows “
That √2 is there because when you actually do a measurement, the probability of finding a particular state is the coefficient squared. This is called the “Born Rule“, and don’t worry about it. Those √2’s are mostly just clutter.
How to quantum teleport the state of A onto C.
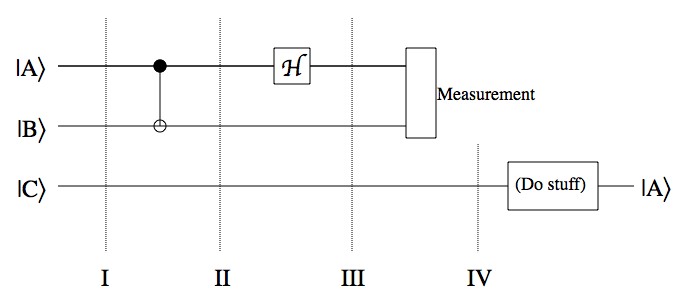
The initial state of all three qubits, “I” in the picture above, is:
Where the state of A, 
Notice that after the CNot gate the qubits can no longer be factored apart, the way the state at I could be factored. This is symptomatic of entangled systems. Next comes the “Hadamard Gate”, which only exists for quantum systems. CNot gates can be done in a regular computer, but the Hadamard Gate is all quantum, baby. Here’s what it does: 
This can be rearranged a bit,
Now when A and B are measured, they can have one of four possible results, 00, 01, 10, and 11. When a measurement is made, then what remains are all of those states consistent with the measurement. For example, if A is measured to be 1, then the state remaining is 
Each of the four results will mean that C is left in one of four states:
If the person in charge of C (the Custodian?) is then told the results, no matter how far away they are, they can perform some basic fixes. For example, if the result is 00, then they leave the state alone. If the result is 01, they run C through a Not gate (which switches 0 and 1). For the others a “Phase Gate” (another quantum-only kind of logic gate) is used, which takes 
Here’s the important bit. Just like the “classical teleportation” above, without knowledge of what the results of the AB measurement were, the person in charge of C (the Controller?) can’t turn C into the original A state. If they were to measure C, without doing any of the fixes, they’d find that the probability of getting a zero or a one is exactly 50%, instead of |α|2 and |β|2 which it should be (again, by the Born rule). Each of the four measurements are equally likely, and the chance of getting a “1” is the sum of chances from each state: 0.25(|β|2+|α|2+|β|2+|-α|2) = 0.25(1+1) = 0.5 (since |β|2+|α|2=1).
You may suspect that there’d be some way to manipulate C, without getting the results of the measurement, that would allow you to overcome this lack of information. Turns out: nope. It’s much harder to see why, and it dips into quantum information theory, but the proof is fairly “straightforward”. This is just for those of you who really feel like looking this stuff up, so it’ll be fast.
The “probability density matrix” for C, before any information is received, is ![\left[\begin{array}{cc}\frac{1}{2}&0\\0&\frac{1}{2}\end{array}\right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B%5Cbegin%7Barray%7D%7Bcc%7D%5Cfrac%7B1%7D%7B2%7D%260%5C%5C0%26%5Cfrac%7B1%7D%7B2%7D%5Cend%7Barray%7D%5Cright%5D&bg=ffffff&fg=000000&s=0 "\left[\begin{array}{cc}\frac{1}{2}&0\\0&\frac{1}{2}\end{array}\right]")
So once again, without ordinary communication, nothing about A is conveyed to C, and if you only had access to C, you’d never know that a measurement was even done.
*Not really. When quantum systems interact they become entangled. From inside of a system this looks like “wave function collapse” which causes no end of paradoxes and problems, but from outside of the systems involved interactions don’t cause collapses, just entanglement. There’s a whole post about this brain trip here.
The other really cool thing about quantum teleportation is that when particle A is teleported, it can be entangled with a further quantum system Q, and that entanglement “survives” the teleportation process. That was a mind-bending realization…
Sorry if this is a dumb question, do we at some point learn what alpha and beta were?
You say for example “if the result is 00, then they leave the state alone”. So how do we get from C being in the state of a|0> + b|1> to 0?
Or wait, a and b are related to probabilities of whatever original A was. So, still looking at the first result in that table, you could still get either 0 or 1 for C. Even tho the A in your AB reading is 0, because that’s not the original A but something that came out of the Hadamard thing?
Am I on the right tracks at all?
@R9: Nope! However, through a lot of repeated measurements of identically prepared states we can get close. It’s a lot like finding out if a coin is heads/tails 52/48 percent of the time. It takes more than one flip.
@R9: The tracks you’re on sound like the right tracks!
I have a different form of the ‘communication’ in that the test of B always reveals the state of C so I comment here just to relieve me of my confusion. That the test is always available and is completely certain. The test on B is always before the test on C but not necessarily greater than the light time for the distance apart of the two tests. Then as the test rsult of B is revealed the state of C is set and revealed moments later in that test on C. Now it might appear that the result of B has to be sent to the site of the test on C before the ‘information’ carried in B & C is communicated. But the only information that is needed is the lenngth of that light time distance in time. And then to use the same tests and sequences to transmit a ‘key’ that had already been moved to the B test site.
The problem is my concept that a test on B sets C instantly and the test can be chosen to set B on one state or another reliably. So I just have to work out why I wrong and the answer given above is more correct.
Thank you.
Just to make clear, because I don’t have a ‘test’ which sets the states of the particles in the entanglement without disturbing the entanglement for the purposes of the communication and, but less important, no test to discover the state of a particle without disturbing that state in the test I cannot use the entanglement to move information over the entanglement faster than light. Now the trick would be to prove that this is always going to be the case and that no tests could be devised that would read states without disturbance and set states without disrupting entanglement. But you admit that your answer is not that exhaustive.
If B and C are entangled, then no measurement on the entangled state can have a definite result. If you could decide the result of the measurement before making it, then you could convey information. Unfortunately that isn’t the case.
The procedure in the last so-dense-it’s-practically-useless paragraph applies to entangled states in general to show that information can’t be conveyed directly.
My head is still spinning. This sounds awesome. So does particle tunneling really work like throwing a brick thru a glass and the brick lands intact on the other side without damaging either the glass wall or the brick?
Also how does all this spooky stuff tie in with the Heisenberg Uncertainty Principle?
Quantum Teleportation doesn’t have too much to do with the Uncertainty Principle. If you really cross your eyes, then you could argue that the randomness of the measurement of A and B is a manifestation of Uncertainty.
Quantum tunneling is yet another very different effect, that does involve things passing “impossible barriers”.
So why can’t you purposefully make a change to “coin” A and have someone record the quantum entangled “coin” C. Would this be faster than light communication?
That change to A has no effect on B.
I assume the “phase gate” you give is for the result 01 but n0t for 11 which seems it should be !0>goes to !1> and !1> goes to -!0> (Sorry, no vertical lines or arrows on my keyboard).
The problem I have in thinking about this ‘communication’ is precisely that the entagled A & B is the same state. Then a measurement will determine simultaneously A & B but not necessarily communicate any information. But that the measurement can occur at the location of A and yet determine B that may by then be some distance way. Still no ‘communication’ occurs. The notion I have stuck in mind is that the outcome of the measurement may be fixed. Then the state of B would also be fixed even if there is no intention to communicate. And then use this ‘fixed measurement’ as many times on sequences of As & Bs until a communication occurs. So what I’m worried about is how I got the notion that the quantum mechanical measurement can be fixed. Someone must have said somewhere that ‘we can make the state of A by the measurement a certain value.’ A statement which I must have taken at face value without thinking. I’ll read what you have written again and see if I can understand their ‘unique’ state fixing quantum mechanical observation.
Very nice explanation, thank you, each time I read it over it makes more sense, that’s a good thing. Could you relate these examples to Bell’s inequality, in the first classical example it must be obeyed but violated in the quantum case, I presume due to the mixed states? Second question, in the few papers I’ve read trying to understand the situation it is often stated the quantum result is a real blow to “local realism”. After reading your explanation the blow seems to be to predetermined states as with the coins in the classical case. Reality and quantum mechanics, where ever you happen to be located seems just fine, am I missing something or just hopelessly lost? Thank you for any help here.
http://news.bbc.co.uk/1/hi/sci/tech/3811785.stm
so I have to wonder what’s going on!
this is good article.
here is the best explanation. https://www.youtube.com/watch?v=zsWKZY2RR28
sorry I gave wrong link. here is the correct one.
go to the library to requst basher quantum phsyics.
Is another form of quantum teleportation quantum tunnelling? Say of photons http://en.wikipedia.org/wiki/Hartman_effect . in this instance a particle disappears at one point and reappears at another. The transit velocity can exceed the speed of light. I don’t understand why this cant be used to transmit information faster than the speed of light, any comments please?
@richard dow
Quantum tunneling is a different effect. But even in tunneling, the particle doesn’t “jump” faster than light. Mathematically, the particle’s wave function acts more like it’s “oozing” through barriers.
Hi. You have a great site here.
And I have a few questions regarding entanglement.
Let’s say that B and C are entangled. Let’s say that state we are interested in is spin or polarization or something we can change. Can we change those states on purpose?
Can we for example set the spin of B to 1 on purpose?
If B and C are entangled, will C show spin 0 after measurement?
@Zexx
Entangled particles aren’t “connected”, they’re correlated. It’s a little like you an a friend having identical letters; you’ll find that if you both look at them they’ll be the same, but if you change yours it has no affect on your friend’s (other than the letters no longer being correlated).
Same sort of thing with entangled particles.
Looks like your conjecture that A can’t influence B is wrong. It can, and instantly (faster than light).
http://www.pnas.org/content/110/4/1221.abstract
Pingback: Q: What is the “monogamy of entanglement”? | Ask a Mathematician / Ask a Physicist
In your explanation on the answer gravy section. Isn’t B and C supposed to be entangle first. But your initial state I has C completely separated by B. You start with entangle A and B. Where did B and C get entangled.
@leo
Exactly right, B and C need to be entangled first. I didn’t include that step because entanglement is generally treated like a resource, kinda like how discussions about cars don’t usually include how to create gasoline.
That said, there are a lot of different ways to produce entanglement. For photons, one of the more common methods is spontaneous parametric down conversion.