Physicist: For those of you not hip to the calculus groove, here’s what’s going down: The derivative of Y with respect to X, written 
If you describe volume, V, in terms of the radius, R, then increasing R will result in an increase in V that’s proportional to the surface area. If the surface area is given by S(R), then you’ll find that for a tiny change in the radius, dR, 
You can think of a sphere as a series of very thin surfaces added together. This is another, equivalent, way of describing the situation. Each layer adds (surface area of layer)x(thickness of layer) to the volume.
You can think of this like painting a spherical tank. The increase in volume, dV, is the amount of paint you use, and the amount of paint is just the surface area, S(R), times the thickness of the paint, dR. This same argument can be used to show that the volume is the integral of the surface area (just keep painting layer after layer).
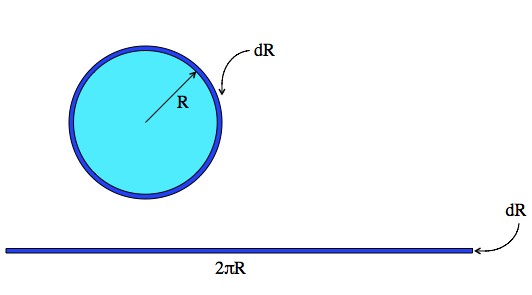
It’s a little easier to keep track of what’s going on with circles.
If you increase the radius of a circle by a tiny amount, dR, then the area increases by (2πR)(dR).
The same “derivative thing” holds up for the circumference vs. the area of a circle. The change in area, dA, is dA = (2πR)dR. So, 
This, by the way, is one of the arguments for using “τ” instead of “π”. τ = 2π, so the area of a circle is 
Answer gravy: By the way, this argument is only exact when the thickness of the new layer “goes to zero“. Basically, the top of the new layer is a little longer/bigger than the bottom of the new layer. So if the area is 
This extra little 
Cool. Wonderful answer to my question.
It happens only in calculus. I only thing I would like to say is thanks to Newton for his ingenious discovery of Calculus !
Very cool. I never thought about this before. But after this explanations it fits together so easily. Thank you
“Volume is the integral of surface area.”
To me, that makes so much more sense that “surface area is the derivative of volume.” Either way, this answers something I’ve been wondering about for a while. thanks man.
It’s easy to visualize in 1D, too. The sphere of radius r and center x is an interval (x-r,x+r), which has ‘volume’ 2r and ‘surface area’ 2: the two endpoints is the boundary. And you can get the former by integrating the latter in the obvious way.
Hyperspheres somewhat less easy, though.
Pingback: Q: Why is the area of a circle equal to πR2? | Ask a Mathematician / Ask a Physicist
not to mention the derivative of the circumference is 2 pi which is the amount of radians equal to 360 degrees
Thank you for this wonderful explanation. However, I don’t know calculus. So can you explain some of these relationships between radius, circumference, area, circle, sphere surface area, and sphere volume in other terms, possible algebraic or geometric?
To me, pi is the factor that accounts for the curvature of a circle as opposed to the straight lines of a square. That is, instead of four times the side of a square, which gives you the perimeter of that square, you use pi times the side(side being equal to diameter of inscribed circle) to give you the circumference of the inscribed circle.
ie: circumference = 2πr = πD perimeter = 4D Circle/Square = πD/4D =π/4
Should not this relationship, somehow, carry through to a sphere vs a cube??
@Tsi:
There is no algebraic explanation for it given that it’s a circle, or namely, a curve.
Say we have a cube C with an inscribed sphere P in it. We know V(P)=4pi*r^3/3 and V(C)=s^3, with s=2r=d, so that V(C)=(2r)^3=8r^3. If you want the ratio of the volume of P to the volume of C, then:
V(P)/V(C)=(4pi*r^3/3)/(8r^3)=4pi/(3*8)=pi/(3*2)=pi/6
If you want to do the same for the area as you did with the circles and squares, then:
S(C)=6s^2=6(2r)^2=24r^2; S(P)=4pi*r^2. You want the ratio, so:
S(P)/S(C)=4pi*r^2/24r^2=pi/6, which equals the ratio in volumes as well.
Circumference and perimeter are not directly related to surface area here nor to volumes, so that’s why pi/4 cannot be brought over. However, because the surface areas are directly related to each other via intergration/differentiation, we can still see a common ratio. The are of a circle differs from the area of a sphere, and so does the area of square from that of a cube. If you were to obtain circumference from a sphere based on surface area, for instance, the formula would be (after much simplification) C=8pi*r, which is 4 times bigger than 2pi*r . Taking the perimeter of a cube based on its surface area, would give us P=48r, which is 6 times bigger than the usual 8r.
Although, you could make the case that because the circumference is now 4 times as big, and the perimeter six times as big, you could use proportions to relate the ratios for sphere:cube and circle:sqaure by 4/6=2/3. Since you obtained pi/4, then the ratio of sphere:cube must be 2/3*pi/4=2pi/12=pi/6, which is what I obtained earlier. So, with the right calculations an proportions, you could relate the ratio of circumference:perimeter to the ratio of sphere’s volume: cube’s volume. Very interesting question.
For everyone, to understand better
About the part he said
“If you describe volume, V, in terms of the radius, R, then increasing R will result in an increase in V that’s proportional to the surface area.”
Means that V/S=R/3, which means the volume and area have a linear relation, even though both are not linear.
And it can be extended to the 1 and 2 dimensions, which are circumference and area, respectively.
A/C=R/2, which, the same way, means area and perimeter have a linear relation, even though area is not linear and perimeter is linear.
To the point: linear is just a concept and it’s relative, like derivative, we need to have another variable to relate with. Knowing V and S have a linear relation => dV/dS=K. And the same way, A and C have a linear relation => dA/dC=K2.
why isn’t the area of the sphere also 2 times the antiderivative of the surface of a circle. the way I calculated it , I found it to be 4 time it.
@anime cheikh med:
What do you mean ‘also’ 2 times the anti-derivative? The relationship between a particular type of measurement of a sphere to same type of measurement of a circle is always 4, never 2. The volume of a circle would be V=pi*r^3/3 since A=pi*r^2 and V = anti-derivative[A(r)*dr]. Of course, this always turns out to be zero, because the difference in the radius is zero since circles are only two dimensional; that is, the third dimension of a circle, when measured, is z = 0. Note, however, that the theoretical volume of a circle is 4 times smaller than the volume of a sphere, which is V=4pi*r^3/3. Perhaps the better question to ask is: why, in general, is the ratio of a sphere to a circle, both with equal radius, always equal to four?
Circles with thickness become cylinders: V = pi*r^2*h. If we were to put a sphere on the inside of this cylinder with the same radius, then we would figure out that h=d=2r. Thus, V=2pi*r^3. Now you see that the ratio of the volume of a sphere to the volume of a cylinder is 2/3.
The area of a cylinder is A=2pi*r^2 + 2pi*rh = C(r+h) = C(r + 2r) = 3rC. The area of a sphere is A=4pi*r^2 = (2pi*r)*2r = 2rC. The ratio of the area of a sphere to the area of a cylinder is curiously also 2/3. This happens due to the natural differentiation relationship between volume and area. If we have sphere P and cylinder D, then we can calculate their volumes, areas, and circumferences respectively. That means we can also calculate their ratios. V(P)/V(D)=K, where K is some constant. Thus V(P)=K*V(D). If we differentiate both sides, we obtain dV(P)=K*dV(D). The K stays because of the coefficient rule of derivatives. Differentiating each volume formula respectively will simplify into dV=S*dr, so S(P)*dr=K*S(D)*dr. The drs will disappear since they are the same on both sides. This is why the relationship between measurements of both figures remain the same. Do not forget that circles are just cylinders with zero height.
I want to add some information that may be interesting even if useless.
I wrote a response above talking about relationships between measures of the same kind on different circular figures with equal radius. We established that circles are cylinders with h=0 and that dV = S*dr. We also know that the ratio of spheres to circles is 4, while the ratio of a sphere to a cylinder with h=d is 2/3.
What I have noticed is that both figures, when circumference is calculated as a derivative of surface area, yield a circumference formula that multiplies the real circumference by some number. This number, we will call it “scale”, represent it by K, and it is given as a relationship. This scale will depend on the height of the cylinder. Thus K is in reality a function of height that multiples the real circumference to produce surface area. K(0) = 1, for circles, thus C=2pi*r just as it should be. For cylinders with h=r, K=4, since it has the same surface area formula as an sphere. For cylinders with h=2r, we know that S=6pi*r^2. Differentiating both sides will yield C=12pi*r. Dividing then both sides by 2pi*r yields K(2r)=6. For h=4r/3, when the volume of the cylinder is the same as of the sphere, K(4r/3)=14/3. We need to try find out why does K change with respect to height — which at the same time, we will treat as a function of the radius.
Keep in mind that the circle is cylinder with h=0 and that the area of a cylinder is given by A=2pi(r^2+r*h). Differentiating both sides gives us dA/dr=2pi(2r+r*dh/dr+h)=2pi(r[2+dh/dr]+h)=2pi*r(2+dh/dr)+2pi*h=C(2+dh/dr)+2pi*h. We have now derived a formula for dA/dr, which is the apparent circumference, which includes K in it. Now, note that h is a linear function of the radius — or at least in our examples, the function is linear. Thus h=xr, where x is the slope that will produce height from radius. With that in mind, we know that dh/dr=x. Now we can substitute in, and things become much more clear: dA/dr=C(2+x)+2pi*xr=C(2+x+x)=(2x+2)C. Dividing both sides by C now yields K: 2x+2, where x=dh(r)/dr. We know this simplifies to K(0)=2(0)+2=2. Though this differ from our original established value, we need to keep in mind that cylinders have two circular faces. Hence, if h=0, we will have no lateral face, only two circular faces. The formula yields the circumference of both circular faces. One circular face would then be half of that, thus K(0)/2=1. This verifies part fo our formula. For every other case, h>0, thus K(x)=2x+2, x=dh/dr. In order to formally express this, we convert K into a piece wise function: K(x)={0 => x=0, 2x+2 => x>0|x=dh(r)/dr}. Now, using the previous values for h, we can obtain x, and verify that this equation is true in absolutely every case:
h=r => x=1 => K(1)=2(1)+2=4, which we already defined as true.
h=2r => x=2 => K(2)=2(2)+2=6, which we already defined as true.
h=4r/3 => x=4/3 => K(4/3)=2(4/3)+2=14/3, which we already defined as true.
Actually, we can correct the anomaly that occurs at h=0. Setting x=-1 solves it: this implies that h=-r; therefore, r=-h. A negative height places the second circular face of the cylinder in a non-existent plane, eliminate this second face and leaving us with one circle, for a factor in the circumference formula. At h=0, while t=both circular faces are the exact same circle, the formula still recognizes that they are two circles in the same plane due to zero height. This ensures that K(x)=2x+2, x=dh(r)/dr holds true for a circle.
We have found an equation that explains why do tridimensional objects yield circumferences increased by some constant factor despite having their circumferences equal to that of a circle with equal radius. Although spheres are not cylinders, there is a direct relationship between the surface area and the volume of spheres and cylinders, which is why it also works for spheres and for cones (cones also have the same relationship with cylinders; that was discovered by Archimides).
No one ever talks about the fact that the product of the circumference of a circle (one dimension) the area of any ball of ‘n’ dimensions will give the area of the n+1 cover of a ball in n+2 space. Why would 2piR be a universal multiplier?