Physicist: This question usually comes in the form of “are complex numbers real?” or “are negative numbers real?” or something along those lines. Turns out you can answer all of these questions at once (if you make up a nice enough definition for what “real” means).
If you think of “realness” in terms of what can be touched, or observed, or measured, then numbers (all kinds of numbers) are clearly not real. That is, numbers don’t phyiscally exist anywhere. No beachcomber will ever discover a new number during the practice of their venerated craft. That said, many people would say that “natural numbers” (which are 1, 2, 3, …) are real in the sense that you can find examples in nature of 3, because you can see (for example) 3 turtles together. Hence the name: natural numbers. By the same note, imaginary numbers don’t exist, because you’ll never see turtles (where
) in nature.
Numbers (math in general really) are all about describing patterns. Regular numbers are great at describing some things (like how many turtles are around), but there are a lot of patterns in nature that can’t be so easily described and require different kinds of “mathematical objects”, like negative numbers, non-integer numbers, complex numbers, matrices, polynomials, lots of stuff.
“3” seems to be a nice and solid property of the group of turtles in the picture above, and “3” seems pretty “real” as a result. You can move the turtles around, rename them, paint them, whatever, and you’ll still have 3. But there’s nothing terribly special about the property of having a certain number of things. Something like a knot, for example, has properties that are very real but are better described by polynomials. The “Alexander-Conway polynomial of a knot” stays the same no matter how you change the knot (any change that doesn’t involve cutting).
By the way, this isn’t particularly advanced math and you can learn it yourself!
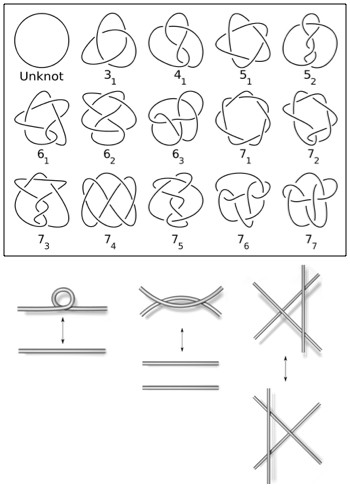
All of the simplest knots, expressed with the least number of crossings, and the “Reidemeister moves” which change what a knot looks like, but don’t actually change the knot itself. Each of these knots (and a lot more) have their own polynomial.
So (and this is the answer), if things in math are “real” because they describe simple properties of things we can see, then natural numbers are no more or less real than polynomials. The same kind of argument can (probably) be made for all of the other weird structures in mathematics. It’s just that the number of turtles is a much more obvious property than, say, the topology of a turtle’s plumbing (polynomials or lists of numbers), or its age (real numbers), or its ancestry (graphs). The quantum mechanical wave function of a turtle (or anything else) is described using complex numbers, because trying to do quantum mechanics without complex numbers is practically impossible. About as hard as counting turtles without the (obviously “real”) natural numbers.
The turtle picture is from here.








I find it helpful to think of math as a language. It’s descriptive, it’s a property of intelligent minds trying to understand and quantify things, but without intelligence around it ceases to exist.
Numbers are abstract entities and counting is the physical act representing those entities. We can’t count anything, including turtles, without them. One doesn’t see the number ‘3’ walking along the beach only the representation(s). But human beings don’t use numbers in the first instance but ‘classes’. We have to classify something before we do anything else; ‘that looks like a table’, ‘this is a turtle’ etc.
This is just the way we think and this is where Set Theory was used to explain numbers at the fundamental level. On the philosophical level it remains undecided as to whether this was successful or not.
But then what is Existence? One could say that numbers do exist and become reality when the are written down but then if we admit THAT then we would also have to admit Unicorns and other fiction become reality when the too are drawn.
I am sure the debate will go on and on.
The argument for numbers not being real comes from the fact that numbers are ideas, but we only think of them as ideas because they are a clear, and generic idea.
If people realized that “Car” is an idea all the same, they would probably change their mind. A car is just an arrangement of many different things, a pattern. In reality, a car is actually many different atoms and molecules in a large pile, and literally wouldn’t be any different if it were disassembled or melted or crushed, other than that the pattern is changed. In the same way, three is the same thing, a pattern, except lacking a physical orientation, or object description, which we tend to add on later.
So cars and numbers are just as real as one another.
I would like to point out that many people, inlcuding myself, consider “0” to be a natural number. Just saying. 🙂
Most of us would agree from the photo within the physicist`s answer that there are three (abstraction?) turtles (another abstraction?) in a human (abstraction) hand (abstraction). The question posed was whether numbers are real, I looked up the definition of “real” which is commonly defined as “actually existing as a thing”, looked up “exist” (etymology is: to step out, to emerge) and “thing” (defined as: that which is considered to exist as a separate entity). To expand on the original answer, you could say: do the concept of numbers exist in reality, or are they merely mental abstractions (definition: existing in thought but not having a physical existence)(etymology: from latin “to drag away, detach, divert”)
Now back to the photo, the things identified as “turtle” and “human” are common name labels for a repeating pattern, in Biology more rigorously classified into taxonomic ranks (Kingdom, family, genus, species, etc..) however it would be enlightening to delve into what is commonly known as “the species problem” in the biological sciences – which is a large topic unto itself, but in summary is an existential problem of there not being a clear cut definition of “species”, that most of these identified life forms on the planet refuse to conform to the general definition of a reproductively-isolated group of organisms. It might be easier to perceive “turtle” and “human” as abstracted from the concepts of “species” and “organism”…. a little harder to perceive “hand” and “three” as abstracted from the concept of “existence”…. you could contemplate the constant and continuous exchange of molecules, atoms, energy, that occur into your hand from the outer environment, and vice-versa. What seems to be a solid barrier between “hand”, “turtle” and “environment” are distinctions that aren’t based in reality, just in our minds. Maybe there is no such thing as inside and outside, that the two are really one, just one continuous flow of matter/energy in what we could call “the environment”? On the other hand, the mere fact that we can perceive with our minds in this way should be self-evident proof that these concepts have a basis in reality. ? Science quickly meets philosophy whenever the axioms within science are consciously examined.
Numbers were made to describe our environment and universe. So numbers aren’t real, in the same sense that a word is real. The object that a word describes is real, but the word itself is made by the human mind and imagination. Numbers can be treated in the same way.
Numbers are as real as the point on the wave that can be measured.
Numbers are concepts. humans think in terms of classes and groups of objects rather than in terms of the objects themselves or specific properties (unless that property is common to some class).
in that sense it is far easier to construct ‘groups’ or ‘classes’ of objects that come singular (1), or in pairs (2), or in triplets (3) and so on. this maps to mathematical objects nicely; most easily to set theory.
details aside we think of natural numbers as a set of all the possible groups we can visualize that objects can be found in, ie, countable quantities. negative numbers are a simple expansion (integers) as are rational numbers (class of objects that needs two integers to describe). and let’s be frank, even amongst those who know what transcendentals and irrationals are and represent, we can’t give a clear answer to their reality. but again, they can be found in nature (phi / golden ratio for instance; irrational yet “natural”).
A number is a symbol for a spike on a graph or a point on a wave. It is a frequency point where a wave can be measured.
Hello,
No. Numbers are not real but can have a real effect on our lives if we assign them real values. The perfect example is the acceptance of something invented called money, and to go along with it, the assigned money value for everything.
It has been taken for granted to be real so we are all poor because it tells us most of us cannot afford anything far beyond what is necessary for us to survive. And only because we can ‘buy’ those things to keep us alive. All this is because we have believe a lie, that the fantasy numbers floating in the sky are real, so they control us.
There seems to be a relationship between numbers, philosophy, infinity and perhaps physics. Seeing and feeling air is not a natural task. We can see water vapor, dust and leaves, in “air”. We can hear sounds in air or feel changes in pressure and detect the effects of the movement of air. In a stillness of pure atmospheric gasses, perhaps within an enclosed, clear, container it could be debated whether or not “air” is present. It is only by breathing, barometric pressure, atomic weight, deflection or absorption of colors and a multiplicity of scientific testing that will determine that air is present. Things that can be seen and counted using natural numbers may give a conceptual perception of uncounted living things or non-living items. If you see three female mammals, how do you count their developing fetus’ soon to be born? They are present, though not seen. The products referred to as “Russian dolls” do not all visually appear when nested, so they cannot all be counted. These demonstrate that even natural numbers are both real and a conception.