The original question was: Here’s my current dilemma: how does one rigorously prove the invariance of the space-time interval? In Taylor & Wheeler’s Spacetime Physics, they basically show one very good example of the invariance, then they instruct the reader to take it as gospel (In case you don’t have their book completely memorized, go here and read pg 22-25). They then use the interval’s invariance to develop the Lorentz transformation. I did a smidge of research online, but I can’t find an argument that doesn’t use the LT to prove the interval’s invariance. Is it possible to establish the LT without the invariance of the interval?
Physicist: It’s worth noting real quick that this post is aimed at people who have recently taken intro relativity. That said, if you’re hip with pre-calc, then you’re ready for the basics of special relativity (like this post).
The regular distance, D, between two things located at the points (X1, Y1, Z1) and (X2, Y2, Z2) is found using D2 = (X1-X2)2 + (Y1-Y2)2 + (Z1-Z2)2. This is basically just the Pythagorean theorem.
But when relativity came along it became important include time, T, along with the the three spacial coordinates, X, Y, and Z. An “event” is something that happens at a particular place and time. So, event 1 happens at (X1, Y1, Z1, T1) and event 2 happens at (X2, Y2, Z2, T2). The timespace interval, S, is found using S2 = (X1-X2)2 + (Y1-Y2)2 + (Z1-Z2)2 – C2(T1-T2)2 = D2 – C2(T1-T2)2, where C is the speed of light and D is the regular (space-only) distance between the events.
What’s tremendously exciting is that not only does the interval stay the same when you change your coordinates through a rotation (regular distance does too), it stays the same when you change your coordinates through motion. This property is why the spacetime interval is so stunningly useful, but it’s also a little tricky to prove. You can prove it using only the fact that the speed of light is always the same (regardless of how you’re moving). What follows isn’t a particularly slick proof, but it works alright.
Things moving at different speeds disagree about where and when things happen. For example, if someone drives by in a car with a blinking turn-signal, they’d say that each of those blinks are happening in the same place (since the driver is moving with the car, and the lights are built into the car, the signal lights are all stationary to the driver), but someone on the side of the road would say that the blinking light is tracing out a dashed line in space (the blinks happen in different places as the car drives by). The driver and the pedestrian are said to be in different “reference frames” and, for example, we could accurately say things like “the distance between the blinks in the driver’s frame is zero”. So, when you’re trying to remember how things can be in different places in different frames or even what frames are, just think: driver/pedestrian.
When considering different coordinate systems we indicate the difference using apostrophes, like this: (X, Y, Z, T) vs. (X’, Y’, Z’, T’). In (almost) everything that follows the Y and Z coordinates will be ignored, since including them just clutters up the math. So events will be written “(X, T)”.
There are three cases to consider:
Light-like, S2 = 0
When two events, (X1, T1) and (X2, T2), are “light-like separated” they’re far enough apart and happen long enough apart that a light beam could travel from one to the other, with no time to spare. Event one could be a photon being emitted, and event two could be that photon hitting something. So, which implies that C|T1-T2| = |X1-X2| which implies that 0 = (X1-X2)2 – C2(T1-T2)2. But, if the speed of light is always exactly the same, then in a different frame of reference
.
Not much to this case. If things are light-like separated, then the interval is always zero, and 0 = 0. Done.
Time-like, S2 < 0
How can a squared number be negative? Don’t worry about it. It’s never necessary to actually solve for S, so S2 serves just fine.
When two events are “time-like separated” they’re close enough together in space, and far enough apart in time, that by traveling at the right speed you can make both events be in the same place. The “blinking turn signal” example is a bunch of time-like separated events, and the driver sees them happening in the same place.
In order to use the fact that light travels at the same speed in all reference frames it’s important to include a light beam in your example. In the “primed coordinates” we make the events happen at the same place at different times, and in the non-primed coordinates the events happen wherever.
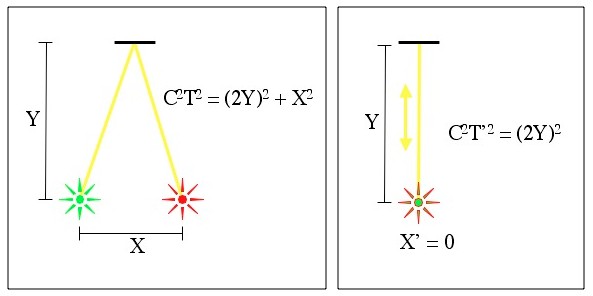
Two events (green and red stars) linked by a beam of light starting at one, bouncing off of a mirror, and arriving at the second.
The total distance traveled by the light beam in the first frame is (by the Pythagorean theorem) , and at light speed the time it takes to cover this distance can be found with
.
In the second frame (with primed coordinates) the total distance traveled is just 2Y, so
What this means is that the interval measured in any frame is the same as the interval measured in the frame where the events happen in the same place (and S2 = -(2Y)2). So, the interval is the same for any frame.
Alternatively, you could make the argument that since Y is unaffected by movement in the X direction, is constant since Y doesn’t change.
Space-like, S2 > 0
Two events are “space-like separated” when they’re far enough apart that light doesn’t have time to travel from one to the other. In time-like separated events there’s a (unique) velocity that you can move at so that both events happen in the same place. In space-like separated events there’s a (unique) velocity that you can move at so that both events happen at the same time (and in different places).
In “spacetime diagrams” the time direction is up and the space direction is left/right (only one space direction, X, is included). The statement that light always travels at the same speed becomes the statement that light rays always trace out 45° angles (or it does with properly chosen units, and otherwise it always traces out the same angle).
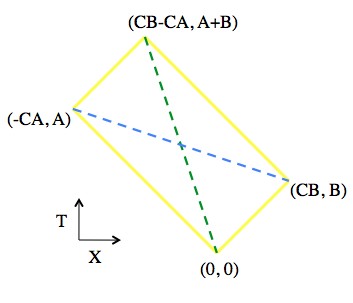
A rectangle made of light beams. The bottom point emits two light pulses. After some amount of time (A and B) each is reflected back, and they meet up at the top corner.
A cute property of the rectangle above is that the diagonals are negatives of each other (when measured with the spacetime interval). Here comes a proof!
For the green dashed line, S2 = (CB-CA-0)2 – C2(A+B-0)2 = -4C2AB.
For the blue dashed line, S2 = (CB+CA)2 – C2(B-A)2 = 4C2AB.
Now, what elevates this fact from “interesting” to “useful” is the knowledge that time-like separated events preserve the interval (last section), and this new fact about the diagonals can be used to show that the interval stays the same for space-like separated events.
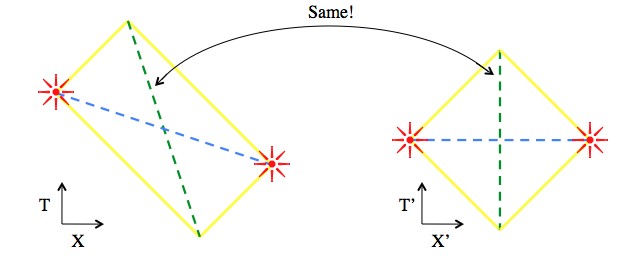
The green lines in these pictures are time-like, and the blue lines are space-like. Since the interval between the two events (blue line) is the negative of the green line, and since we already know that the green lines have the same interval, then the blue lines must have the same interval. This means that the interval between two space-like separated events stays the same when you change your frame.
So, the (space-like) interval between two events in a given frame is the negative of the interval between a particular point in the past (which could send a pulse of light to both events) and a particular point in the future (which could receive a pulse of light from both events). Since these points are time-like separated, we already know that changing frame keeps it the same. Changing frame doesn’t change the relationship between the four events in terms of how light travels between them, so we get another rectangle and another set of diagonals. In the new rectangle the time-like diagonals are the same, so the space-like intervals are the same.
Once you’ve got the spacetime interval in your physicist’s toolbox you can almost immediately derive things like time dilation, length contraction, the twin paradox, the list goes on.







Does anyone think for a second that disagreement “about where and when things happen,” would ever be accepted in traffic court, or anywhere strict rules of evidence are properly enforced?
The driver who, speeding down the road, would say of their blinking turn-signal that “each of those blinks [is] happening in the same place”, would seem unlikely to pass a driver’s exam. Conversely, have we ever heard anyone, including physicists, make a claim that the blinkers are moving relative to the car & driver? Pedestrian, driver, and radar operating traffic cop do not disagree as is claimed, suggesting a better analogy for the basis of justification might appear to be in order.
I disagree. To say that each blink is happening in the same place means that each blink is happening in the same place relative to where the driver is sitting, i.e., relative to the frame of reference defined by the moving driver.
I’m having trouble following the algebra in the Time-like case.
For the first frame, as I understand it S^2 = X^2 + (2Y)^2 – (CT)^2, just following the basic formulation above.
You derive from pythagoras -(2Y)^2 = X^2 – (CT)^2
I put these together and get S^2 = 0, not -(2Y)^2 !!
Actually I’m wondering if I’ve just managed to prove to myself that S-S = 0. Feel free to disregard this if I’m being stupid.
Ok I thought some more and I don’t understand how this works without setting S to 0. 🙁
This is extremely helpful and extraordinarily clear. I’m a physics teacher and you’ve really distilled this information in a teachable way. I thank you greatly for your very well-worded post!
Due to tests having shown that light is always measured as having the velocity of 300,000 kps in any frame of reference, it also, if examined properly, proves that all objects with mass are constantly in motion within the 4 dimensional environment known as Space-Time, and they do so at the speed of light. This leads to the invariance of the space-time interval.
Taking this constant motion into account, a logical full analysis of motion will lead you to having a full understanding of Special Relativity, along with leading you to completing an independent creation of all of the equations that are related to Special Relativity. No education in physics is required at all, other than knowing that the speed of light is the fastest speed possible.
Once done, the physicists will ignore your work due to you having exceeded their accomplishments via pure simplicity.
See http://goo.gl/fz4R0I for what physicists are yet to expose to you.
Pingback: Q: Since the Earth is spinning and orbiting and whatnot, are we experiencing time wrong because of time dilation? | Ask a Mathematician / Ask a Physicist
In all of the above discussion, it is assumed implicitly that the transformation equations are linear. Einstein justifies this by saying that space is isotopic and homogeneous. Would anyone like to comment on how homogeneity and isotropy of space guarantee that the transformations are linear?
I’m not quite sure what the original respondent hoped for in a rigorous proof of the invariant interval, but anyway, here’s my take on the problem.
When Bill walks past the trash can, he sets his stopwatch to zero; and as he approaches the Big Tree, his watch reads “twenty-five seconds”, say.
Since all observers must obviously agree on these readings we call them “invariant” and they have been used to characterize a mistaken value, the “invariant interval”, supposedly given by the watch. This idea contradicts the principal feature of Special Relativity, according to which no clocks measure intervals whose value is independent of some choice of observer. In other words, the intervals clocks do measure, if any, are not invariant.
Call me an old skeptic, but in general it should not be possible to evoke an “absolute” entity simply by establishing mathematical relations between terms. Somewhere along the line, as they say, the rabbit has to get into the hat; and Minkowsi Spacetime is no exception to this rule.
@Stuart G, the stopwatch in question will actually measure the total distance in 3+1 space that it’s moved. This is an invariant quantity–anyone who observes Bill’s motion will be able to see that “the distance in spacetime between where Bill started the stopwatch and the point where he passed the tree was about 1.5 gigameters.” What they won’t be able to agree on is the distance and time components of that vector displacement.
The Time-Like example appears to be Light-Like.
Unless I have misinterpreted it, the two events are a beam of light leaving one point, travelling at the speed of light (as it tends to do) across a distance of 2Y and taking exactly 2Y/C seconds for the journey. Doesn’t that meet all the requirements of Light-Like separation?
@Alan Garrod
If you point a flashlight at the Moon it takes the light about two seconds to get there, reflect, and come back (it’s unlikely any photons would actually get back to you, but if they did: two seconds).
The two events that are timelike separated are 1) you sending the light and 2) you receiving the light. You can tell that these are timelike separated, in part, because a good way of telling the events apart is by looking at your watch.
Thanks, NXTAngl, but you seem to have misunderstood my point, (11 Mar, 2016) which is intended to address the original question as to whether it is possible to prove that the so-called spacetime interval, is invariant.
I intended to suggest that this interval may be entirely imaginary, in the sense of being fictitious, (since I do not see how it is possible to prove otherwise). For example, note that Physicist depends on the idea of the constancy of the speed of light for his explanation above; but Einstein has argued carefully that this was merely a “stipulation” on his part.
Certainly observers will agree that a clock reads “two” whenever it reads two, “three” when three and so on. This much follows from presentations in the literature, but how can you prove that the invariance of the interval amounts to anything more?
Pingback: Q: What is dark energy? | Ask a Mathematician / Ask a Physicist
Hi, Can you please explain why did you draw a rectangle in the “space like” and can you explain why 45° angles and After some amount of time (A and B) each is reflected back, and they meet up at the top corner.
In “spacetime diagrams” the time direction is up and the space direction is left/right (only one space direction, X, is included). The statement that light always travels at the same speed becomes the statement that light rays always trace out 45° angles (or it does with properly chosen units, and otherwise it always traces out the same angle).
A rectangle made of light beams. The bottom point emits two light pulses. After some amount of time (A and B) each is reflected back, and they meet up at the top corner.
@Stu G: There seems to be confusion. no is saying or would say that clocks measure invariant intervals. In fact, they don’t. Two different observers would see two different time intervals. They would also measure two different distances between the events. However, when each of them plugs in their values into the spacetime interval equation the delta S^2 would be same. This is not a clock measurement but a 4 dimensional distance calculation. The time interval and distances are observer dependent.
Pingback: Q: In relativity, length contracts at high speeds. But what’s contracting? Is it distance or space or is there even a difference? | Ask a Mathematician / Ask a Physicist
I’m probably too late to the party, but when you say things like “if S^2 < 0 you can travel at a certain velocity to make both events happen at the same place" aren't you already presupposing some information about the Lorentz transformation? How do you justify this statement strictly from the relativity principle?