The original question was: The five platonic solids (tetrahedron, cube, octahedron, dodecahedron, and icosahedron) are often used in games to make 4, 6,8,12, and 20-sided dice respectively. However, if you renumber the dice using nonnegative whole numbers you can create other pseudo-N-sided dice.
We will call one or more platonic solid dice a “pseudo-N-sided die” if, when we roll them and find their sum they can add to all numbers 1 through N and do so with equal probability. For example:
A cube can be renumbered to be a pseudo-2-sided die.
Two cubes can be renumbered to be a pseudo-12-sided die
Two icosahedrons can be renumbered to become a pseudo-100-sided die
Using any number of platonic solid dice, what is the smallest pseudo-N-sided die you cannot make?
Physicist: A 7 sided die is the smallest that can’t be made using other relabeled dice added together. If you’re not familiar with these games, a “d6” (“dee six”) is the completely standard, cubic die that’s labeled 1 through 6. “2d6” means roll two of these and add them together (like craps).
You’d hope that 1d12 = 2d6, but unfortunately that isn’t the case. Some numbers are more likely to come up (7) and some are less likely (12) and for fair dice each number should be equally likely.
If a sum of properly labeled polyhedral dice can simulate a fair die that would be labeled (1, 2, …, s), then we’ll call s a “D number”. So Right off the bat, labeling the regular polyhedra normally (1,2,3,…), it’s clear that 4, 6, 8, 12, and 20 are D numbers.
The five regular polyhedra: d4, d6, d8, d12, and d20.
Labeling these differently, you get all of their divisors as well. A d6 labeled (1,1,2,2,3,3) is exactly the same as a d3 (as far as generating random numbers is concerned). So, the D numbers are D = {1 (a “doom die”), 2, 3, 4, 5, 6, 8, 10, 12, 20}.
From left to right: a d12, d1, d2, and d3.
The trick usually used for making a d100 (rather than getting one of those giant goofy ones), is to multiply one d10 by ten and add the second. So, 1d100 = 10(1d10-1) + 1d10.
“96” as represented on two d10’s. d10’s exist because people want to generate numbers between 1 and 10, but they are not regular polyhedra. That said, this could be done with two d20’s labeled 1 to 10 twice.
Doing the same to the weirdly labeled dice you can simulate any fair d(xn), where x is any D number. For example, the dice to get a d81 are: (0, 27, 54), (0, 9, 18), (0, 3, 6), and (1,2,3).
So that expands the list substantially (infinitely). The D numbers now include D = {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 16, 20, 25, 27, 32, ….}
You can also get dice of the form d(abc…) where a, b, c are D numbers. For example, to create a d30, you could use either 1d30 = 5(1d6-1) + 1d5, or 6(1d5-1) + 1d6. The dice you could use to get this might be (0, 5, 10, 15, 20, 25) and (1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4,5,5,5,5). You can also get fair d30’s by cheating a little, and building a polyhedra using the same face, but two different kinds of points.
A d30, or “rhombic triacontahedron”, is not a regular polyhedron because it features both 3-edge vertices and 5-edge vertices.
So, every divisor of a D number is a D number, and every product of D numbers is a D number. Rather than listing them, it’s much easier to say: the D numbers are those that can be formed using any combination of the primes 2, 3, and 5. Numbers like this comprise a lot of the lower numbers (9 out of the first 10), but quickly become more and more uncommon (33 out of the first 100). Sadly, there’s no way to construct a fair die with any other prime factor. So, there’s no d7, d11, d13, d14, d17, d21, d22, d23, d26, … The chance that a random, very large, number is a D number is effectively zero.
It turns out that these are the only D numbers. The reason is that, ultimately, you’re dealing with the 5 regular polyhedra, and they determine the size of the “state space”. For example, 2d6 has 36 states (36 = 62). No matter how cleverly the two dice are labeled, those 36 states can never be fairly divided into, say, 5 or 7 outcomes.
The state space for 2d6. Each of the blue squares comes up with equal probability.
The same idea holds true for any number that has prime factors other than 2, 3, and 5, so none of them can be D numbers.
There are of course standard tricks to almost simulate other dice. For example, if you needed to roll a 1d7, what you’d probably do is roll a 1d8 and declare that “8 is a re-roll” (common sense like that is poison to the exotic dice market). In practice, the “re-roll” technique means that real dice can be used to perfectly simulate any non-D-numbered die. For example, you can use a coin to choose between three people by flipping it two or more times: “HH” for Alice, “HT” for Bob, “TH” for Carol, and “TT” for “go again”.
But very technically, it’s impossible to simulate a fair d7 using fair polyhedral dice (same is true for an non-D-number). The best you can do is have seven possibilities that are all equally likely, and an eighth (or more) that is less likely. For example, if you allow up to three rolls, then the only way to have not selected a number from 1 to 7 using 1d8 is to have rolled three 8’s in a row; a chance of 1 in 512. If you could re-roll forever, then the chance that you’ll always roll an 8 is zero. However, if you plan to do anything with your life (other than to accurately simulate one roll of a single d7 using a d8, while also living forever), then at some point you’ll have to stop rolling dice. No matter how long you spend trying, there’s a tiny chance that you never stop seeing 8’s. Therefore, a d8 can never quite simulate a d7, because there’s always a “null-result”. That said, if you see an 8 more than 15 times in a row, then congratulations: you are now the most lucky person ever!
This has nothing to do with the question, but: In two dimensions every die is available; a square is a d4, a septagon is a d7, a tridecagon is a d13, etc. But that’s boring.
In four dimensions the D numbers are the same, because the available dice would be a d5, a d8, a d16, a d24, a d120, and a d600. This is more kinds of dice than can be found in any other dimension! Four dimensions is kind of a paradise for mathematics; just enough wiggle room that surprising stuff shows up, but not so much that it’s boring.
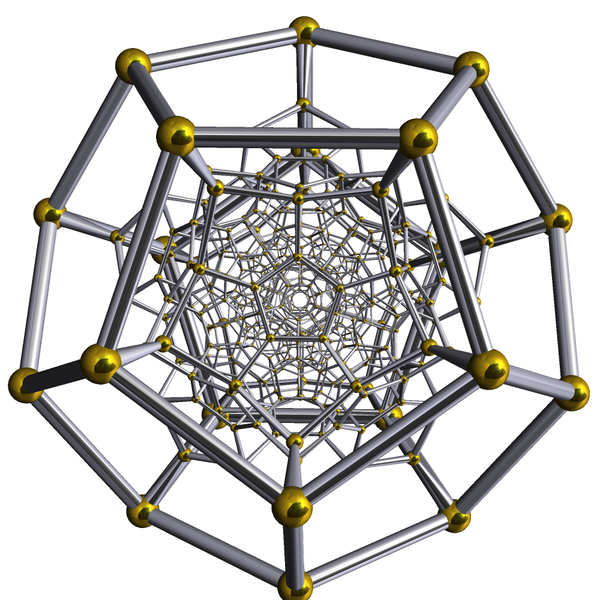
The d120. If you put a light right above one of the faces of a giant, clear d12 you get a funky shadow on the ground. If you do the same (analogous) thing to the d120 in four dimensional space, you get a “shadow” that looks like this. The “faces” of the d120 are the cells contained by the edges and (weirdly enough) the exterior itself.
In X-dimensional space (X=5,6,…), the only dice are the d(X+1), the d(2X), and the d(2^X). These are the higher-dimensional versions of the d4, d6, and d8. So, you can have a d13, but you’d have to go to at least 12 dimensions. In fact, if you want a die with X sides, you just need to be a nerd in (at most) an X-1 dimensional universe.
The purple dice picture is from here.
Excellent summary of solids by Physicist.
However, it is perfectly simple to make a d7 by renumbering. You simple take an octahedral, 8-sided, die, and put ‘re-roll’ on the 8. While, in principle, it is possible to roll an infinite series of ‘re-rolls’, it is just as possible for the die to land indeterminately an infinite number of times. Both are highly unlikely. However, as long as a d8 produces a number from 1-7 with 8 ignored, it will always produce a fair 1-7.
It’s also possible to use 2d6 to produce the numbers from 1-12 fairly. However, this is not done by adding them, but rather by using one die to determine whether or not you add six.
Die one: 1-3 means add 0 to die two, 4-6 means add 6.
Die two: 1-6 with 0 or 6 added, based on the result of die one.
What would be interesting to know would be whether you can formally demonstrate that a fair 7 sided die could not be constructed, or that it could be. Clearly this could not be a platonic solid. Trivially, you can construct a seven sided prism (by projecting a seven sided flat shape) and then rolling it like you would roll a pencil. By exploiting the possibilities of irregular faces, though, could a die-shape, rather than a roller shape, be constructed in such a way that it produced equal probabilities of landing on any side?
But if you can make a fair dice for a multiple of 7, e.g. d35 or d56, doesn’t that mean that effective, d7 can be constructed?
That’s absolutely true, however fair multiple-of-seven-sides dice can’t be made either.
It is possible to create a 14-sided face-transitive polygon and therefore by extension a 7-sided die:
Take the seven points of the form
(cos(2*pi*i/7), sin(2*pi*i/7), 0)fori in [0, 7]. Add another two points(0, 0, 1)and(0, 0, -1). Now you have nine points: take their convex hull.This gives you a double pyramid, with a seven-sided regular polygon as the base for both pyramids, where the two pyramids are glued together.
This polygon has 14 sides. For two faces of this polygon, there is a symmetry operation that moves one face to the place of the other face: if both faces belong to the same pyramid, a rotation will suffice, otherwise, a mirror flip exchanges both pyramids.
Therefore, the polygon is face-transitive, which means that it can serve as a fair die (since all faces are interchangeable, as a physical object the polygon has the same probability for each face to land on that face).
More generally: take an n-sided regular polygon, construct a double pyramid over this polygon with 2n sides, and now label the faces 1, 2, …, n, 1, 2, …, n: you constructed an n-sided die for arbitrary n.
Hi Everyone. Thank you for this terrific forum, for the question, the well-thought out answer, and all the comments. Having analyzed polyhedral/geodesic structures in the past, being bit of a logician with my information science background coming to fruit and partial to probability, and this whole discussion reminding me of way back when I was learning about finite state automata… well, I just had to comment.
One can certainly take an octahedral die and mark one face as “do over”. That works for d7, but I think there is a much easier way. I started to post a little while ago, but retreated to a piece of paper to mull things over, at least with a simple example, and I actually believe I have a solution.
I was considering the equal contribution of each of N number of dice of dX (X is the d number of the dice) to a total sum, and confused myself for a moment concerning the relative frequencies of the respective sums, as they are not equal between the sums between 2 and 12, say, of two (N=2) six-sided (X=6) dice. But, my original idea was to take the mod(N)+1 of the sum, such that the answer will be a natural number from 1 to N. My thinking was that, since each die contributes equally to where the sum lies within the modular space, which essentially constitutes a N-gon, that the final state of the modulo(N) (which side/vertex one was on) would be evenly distributed. As I look at it more (it’s been about an hour or two) I’m evermore convinced that this is completely valid, and corresponds, essentially, to having a six-dimensional hyper-triangular die with seven five-dimensional hyper-faces. It’s evenly distributed, and you don’t need six dimensions.
If we look at throwing two regular dice(N=2, X=6), out of 36 (6^2) possible rolls, we have 1 chance for a sum of 2, two for a 3, three for 4, four for 5, five for 6, six for 7, then five, four, three, two and one for 8, 9, 10, 11 and 12, adding to 36 possible outcomes. Since we have two dice we’re looking at mod(2), so let’s add them and see how many end up in mod(N)=0 (even) and how many in mod(N)=1 (odd).
Mod(N)=0: 1+3+5+5+3+1= 18
Mod(N)=2+4+6+4+2=18
That works. It doesn’t prove my point, but stands as an example. I’ll get to proving it later when I’m a little clearer.
It would appear that, given N number of dice of ANY number of sides, we have equal possibilities of the sum being in any of the N number of modulo states, from 0 through N-1. That is a general solution to this problem. If we throw seven of any type of dice, take the mod(7) of that sum, and add 1, we get an even distribution of the seven numbers 1 through 7. This IS just like sitting though a week’s worth of finite state automata while the teacher confused the people that hadn’t got it, more and more, until she got to finding out whether a natural number was divisible by 7, and I couldn’t pay attention to her anymore and started to scribble. All we needed was N states, no matter what N was. The general solution was simple. She handed out a sheet based on my lesson the next day. Anyway….
Of course, I also like the highly irregular dice with 7 or fourteen sided pyramids on each oblique face. I’ve always liked those…
Please feel free to email. I’d love to discuss this further, or almost anything else of interest to intelligent folk. Like I say, I have other discoveries regarding these shapes, and also need to know more about the specifics of the fourth dimensional analogues. Also, ask me any question, whatsoever. It’ll at least be an interesting conversation, I’m sure.
Thanks again,
and much Peace and Love,
Tony
@Tony “Bones” Orlow
and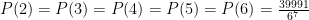 
, which is as close to perfect as it’s possible to get in this case.
Clever! However, your method still runs into issues with the fact that the number of possible “raw results” can never be divisible by 7 (for example). If the number of states were NX, then this could work, but since the number of initial states is X^N (X=2,3,5 or any combination) there’s no way to fairly distribute among 7 outputs. For example, using (7d6 Mod 7)+1 you’ll find that
{;O DOH!
Thanks!
I see exactly your point. That’s why you’re The Physicist (even though this is really combinatorics), and I’m the algorithm guy. Basically all I did was smooth it out as much as possible by making it circular through modulo arithmetic, but without being able to divide the set of equally probable outcomes from regular dice into 7 (or whatever d value), it’s never going to be a truly even distribution in a single throw of the dice. Gotcha. 🙂
However, I would suggest that this slight discrepancy can be immediately eliminated during a game of multiple throws, if the previous modulo value is included in the subsequent sum before taking the next mod. This would smooth out the distribution, and could be preceded by a throw, or some draw of d number of cards or straws. I guess it doesn’t matter exactly how many dice or what kind one throws, as long as the potential sum of a throw is a decent multiple of whatever d one is trying to simulate, and the results are smoothed out as described.
Does that make sense?
Thanks, and keep up the good work!
Tony
You can use 3(3d)-2 to get a result of 1 through 7… Or 2(3d)-1 for 1 through 5… or 5(3d)-4 for 1 through 11. The 3d 8 use looks rather like a three-sided football,each side being a 1×2 unit rectangular face incised at opposite ends with an opposing 90° arc. /)
(/ sort of like this.
Mathematically that’s D=[D-1]/2 (3d) -[D-3]/2. Sorry my diagram above didn’t translate well.
Hi Mr Haumesser. I don’t think 3(3d)-2 will work to simulate 1 to 7. There are 27 possible combinations (3^3) but there are only 7 possible outcomes. Since 7 doesn’t divide into 27, there will be uneven distribution of 1 to 7. In fact there is only 1/27 chance of getting a 1 (1,1,1) and also only 1/27 chance of getting a 7 (3,3,3). And there is a 7/27 chance of getting a 4, more than any other number.
I submit a fair d7 can be simulated with a d12 and any d(even) in the following way.
The d2 determines the interpretation of the number plan on the d12.
When the d2 is even, then the d12 (numbered 1 to 12) is interpreted as (1,2,3,4) = 2; (5,6,7,8) = 4; and (9,10,11,12) = 6.
When the d2 is odd then d12 (1,2,3)=1; (4,5,6) = 3; (7,8,9) = 5; (10,11,12) = 7.
Q.E.D.
Maybe a fair d7 could be represented in base 2 notation, discarding the zero result. Seven is represented by 111, so you could flip a coin three times – once for each binary digit. If you get three tails, start over.
John Stevens, while your answer does get far closer to fair, it is not quite fair. The probability for 2,4,6 ends up being 1/2 * 4/12 = 1/6, and the probability for 1,3,5,7 ends up being 1/2 * 3/12 =1/8, making this combination much closer to fair, but not quite fair.
The main problem with this approach is that 7 cannot be evenly divided by 2, which is what would ultimately need to happen to make any mapping to an even-faced die work.
John Schuhr, while this approach does work, it is ultimately no different than rolling a d8 and declaring that the 8 is a reroll. However, this does open up a different mathematical possibility if you construct Turing machines.
Since a d2 could be converted to binary, and computers run on binary, it is possible to create a Turing machine with them. Now that you have a Turing machine, you could program it to simulate a triangular dice in 6 dimensions, which would give you 7 sides. Since in N dimension you could have a d(N+1), and a Turing machine could theoretically simulate any of these higher dimensions, it is possible to simulate a dN, where N is any natural number, using only d2s. While this method is inefficient and means that many of the d2s would not be rolled randomly (the ones actually used to construct the Turing machine & program it) it proves that it is possible.
I would be very interested if someone found a way to simulate a d7 with only d2s without needing a Turing machine.
What is unfair about rolling 7d20 ÷ 20 for a pseudo d7? I appear blind to an obvious counter argument or explanation. 🙁