Physicist: Nopers! Although that would be an amazingly cool super-weapon.
Physics can be pretty complicated, but what makes physics different from lesser sciences, like Calvinball, is that physics has rules that are absolute. While the consequences can sometimes be difficult to predict (technically, platypi are a direct result of fundamental physical laws), the rules themselves tend to be pretty straightforward. In the case of relativity there are two big starting rules:
#1) All of physics works exactly the same whether you’re moving or sitting still. So, in absolutely every way that counts, there’s no difference.
#2) The speed of a passing light beam is always the same.
There are a lot of bizarre things that fall out of that second rule (generally in not completely obvious ways). Among them is the fact that the equations Newton figured out for momentum and energy, 
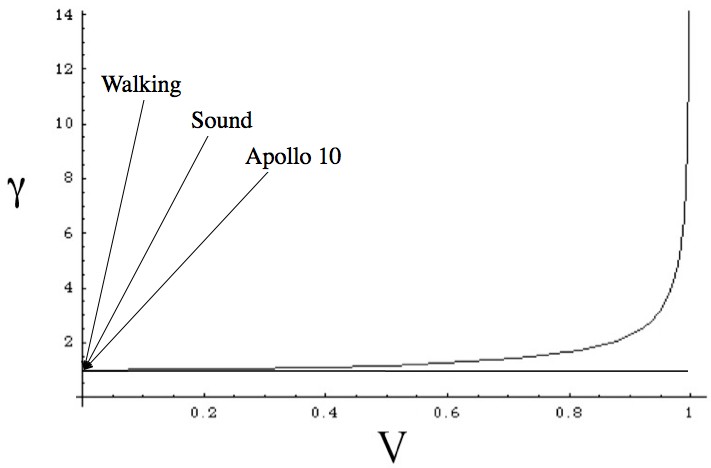
Values of gamma vs. fraction of light speed. Being close to 1 at low speeds means that the “error” from relativistic effects is very small. Apollo 10 is the fastest (Earth relative) any human has ever moved.
So finally, here’s the point:
So long as the particle or object in question isn’t currently slamming into anything that’s moving differently (or “relatively”), then you can just apply rule #1. No matter how fast or slow something is moving, it will always behave exactly the same way it would if it were sitting still. So, if you accelerate a rock to 99.99999999% of light speed (or thereabouts), then it will do exactly what a rock at 0% of light speed does: be a rock. A fast rock, sure, but it wouldn’t suddenly do anything a regular rock wouldn’t. I’m not knocking rocks, they’re fine and all, it’s just that they’re not black holes, which are terribly exciting.
It turns out that gravity is way more complicated than Newton first proposed. The same set of theories (special and general relativity) that accurately predicted that fast objects will behave more massive from our “stationary” perspective, also predicted a whole mess of weird things about gravity. Including the fact that gravity itself always obeys rules #1 and #2. So if a thing isn’t a black hole when it’s sitting still, then it isn’t a black hole when it’s moving.
So, but while it’s there, the things it’s moving past will be drawn towards it by gravity, with an escape velocity greater than the speed of light, but it will be moving so fast that it will just leave their spaghettified bodies in the proverbial dust?
So I guess the follow-up question would be, from an outside observer’s perspective, would it ever appear to become a black hole, since its apparent mass could be arbitrarily increased by bringing it closer and closer to the speed of light? What happens when the apparent mass becomes something ridiculously huge?
Calvinball!!!!!!!!!!!!!! You sir are badass. Physics and Calvin and Hobbes this is too much awesome
To become a black hole you need a certain ‘density’ of mass in a certain volume, going past whats known as the Schwartzchild radius….as you go faster your mass increases, but your length also increases, this spreads the ‘new’ mass over a larger area, so no density increase and no black hole 🙁
@Edward: The mass isn’t actually increasing, it’s just that \gamma*m looks like it’s more massive in Newtons laws. It actually means that kinetic energy doesn’t work the way Newton says it does. It has an extra term, which in Newtons approximation would look like a mass-term. But it really isn’t. It is energy that is conserved if there is a collision though.
Your length does not increase. Not to you, and not to the outside observers who see it decrease.
I think a force is prasent in space opposite to g. force . Comment on it…
relativistic speed questions usually can be resolved by keeping tabs on the gamma term. while most quantities increase with speed (multiplied by gamma), the time elapsed for relativistic objects decreases relative to stationary observers (divided by gamma).
an object moving so fast as to appear as massive as a black hole, would need an enormous gamma term. but, the rate at which time passes for that object, would be reduced by the same amount… a gamma of 1000 means an approximate speed of %99.9999995 of the speed of light. it would mean an object moving that fast would appear to be 1000 times more energetic or massive than it actually is, but at the same time it takes it 1000 times as long to interact with anything (cruedly speaking). if you were to imagine this object beaming light forwards, in terms of power output, the energy per time quantity increased while the time quantity decreased, yielding the same rate value – energy and time are conserved this way quite nicely.
an object moving faster would appear to be more massive yes. equivalently it would appear to age less. if you imagine falling into the gravity of this near-light-speed object that gained black-hole mass proportions (assuming the mass of a stellar black hole, 3x our sun), you would not notice a stronger gravitational field!
the simplified explanation is this: as you’re falling into (onto?) the passing object, your rate of time will have to (eventually) reduce to that of the surface of the passing object. because it is in motion, the mass and time of the object are altered by gamma, so while you would experience a stronger gravitational field, you would experience it over a longer duration, compared to falling into a true gravitational field of such strength. on the whole the two effects should balance, so we can conclude that regardless of the motion of an object the apparent gravitational strength (as agreed by all observers) should remain constant, consistent with relativistic emission power/rate calculations for light, since gravity too propagates at light speed.
If two objects moving near the speed of light relative to each other crashed into each other could they produce a black hole?
@Anders
Possibly/probably!
If a black hole is moving at the speed of light would it become a super black hole?
My problem regarding speed augmenting mass is:
why does the photon going at the speed of light doesn’t have mass”
Why does the neutrino going at almost the speed of light does have so little mass.
Speed really doesn’t seem to produce mass in those cases. Unless its acceleration that produces mass; but then what happens to it when accelaration cease and speed settles?
in the opposite way, is black hole is really something that moved/moving as fast as light?
As a complete novice I have ask this. If your traveling the speed of light, are you not light yourself?