Physicist: First, don’t gamble unless you can be sure you won’t get caught cheating or you enjoy losing money.
Games of chance come in two flavors: “completely random” and “not quite completely random”. It’s not always obvious which is which, and it often barely matters. A good way to tell the difference is to imagine showing the game as it presently is to Leonard Shelby (that guy who can’t form new memories from Memento). If after extensive investigation he always has the same advice (“I don’t know, bet on red?”), then the game is memoryless. “Memoryless” is a genuine fancy math term, and refers to systems where the future results are unaffected by the past results.
Leonard Shelby from Memento. If a game resets and doesn’t “remember” anything, then there’s no overall pattern, and no way to “outsmart” it. For these games Leonard is on an equal footing with everyone else.
Say there are some folk playing a really simple game called “guess the number”. You guess a number, roll a die, and if you guessed right you win. For all its pomp and glitter, this is essentially what gambling is. Don’t gamble.
Now say that a few rounds have already been played, and on the fourth round a 3 is rolled. Lenny would experience that fourth round differently than most other people.
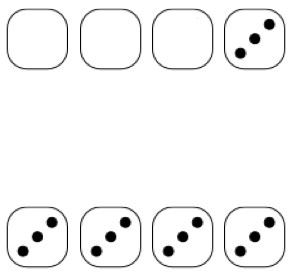
The same series of rounds as seen by someone without memory (top) and as seen by someone with memory (bottom).
Lenny sees a 3 and moves on with his life. He knows that a 3 is as likely as any other number, so he isn’t surprised. It’s only those of us burdened with memory who see “patterns” in these random numbers (fun fact: this is called “apophenia“). Someone who had seen the first rounds churn out a string of 3’s might think that the fourth round will be less likely or more likely to be a 3. However, assuming that the dice are fair, it turns out that Lenny’s intuition is better than ours; the roll of each of the dice is completely independent all of the other rolls.
The chance of getting these four 3’s in a row is 
What we expect to see is what fancy math folk call a “typical sequence“; big jumbles of numbers with no discernible rhyme or reason. Every string of (fair) rolled dice is equally likely and while randomly emerging “patterns” will occasionally show up, they don’t change the math and can’t be predicted. Of course, they do make for better stories.
This is from xkcd. Clearly.
Games like craps or roulette are memoryless, which means that notions like “hot tables” and “runs” are completely baseless. On the other hand, games like blackjack are not quite memoryless. Since the cards are pulled from the same shoe if you sit and watch the cards for long enough you can predict which cards will be drawn next slightly better than someone who hasn’t.
Lotteries are also memoryless. So, assuming the lottery is fair, the only way you can increase your probability of winning is to buy more tickets (but please don’t). Number order and choice make no difference whatsoever. Unfortunately, assuming that the lottery is fair is a big assumption, that isn’t necessarily true. Keep in mind that lotteries, like all organized gambling institutions, are not created so that someone will win, they’re created so that everyone will lose.
If you want to win a lottery, far and away the best way to do it is to set one up yourself (which is illegal almost everywhere there are laws). Not to put too fine a point on it, but people who run big lotteries and casinos are massive ——-s. Gambling is seriously bad news, pretty much across the board (the owners do well).
Statistically speaking, this is a better use for your money than any form of gambling.
There are much better ways to throw away money than playing the lottery. Before you think about giving away no-strings-attached money to people who don’t need it, consider trying: “cashfetti” cannons, recreating that scene from Indecent Proposal, money origami, lighting cigars, lining animal pens, breaking chopsticks, and eating it to gain it’s power.
A lot of folk have written in asking for mathematically-based gambling advice and, details aside, here it is: Don’t. The only way to win is not to play.
Getting off of the strategy topic, because yeah there is no valid strategy for making money in any game where you’re playing against the house (although this article does ignore the question of more skill-based games where you’re playing against other players with a house rake): If the total amount of enjoyment person A gets out of, say, spending $50 on a stamp or coin collection, on books, games, movies, comics, or whatever entertains them is equal to the amount of enjoyment person B gets out of spending time at a casino with a strict $50 bankroll, then aren’t they equally valid options? How is losing $50 at a casino and getting enjoyment out of the time you spent at the casino “throwing your money away” any more than spending $50 on any other hobby or past time? Yes, if you have a problem with gambling or you can’t set yourself a strict bankroll limit, then it’s questionable. But that’s hardly true for most people. There’s an awful lot of groundless moralizing in this article, and I say this as someone that has only ever once been to a casino.
Lotteries are a bit less random than you imply. Because of two factors: choice of number and choice of when to enter.
First, people choose lottery numbers. Payments are split between people who choose the same number. Thus a number which only you have chosen pays more than a number chosen by many people. Thus, if you can predict which numbers people will not pick, you can improve your winnings. A simple way of approximating this is to use a random number generator (like random.org)
Second, people choose when to buy tickets. The full game not just buying a ticket once. It is frequently played as follows: the house annoinces a pot value, everyone chooses a number and pays to play that number. The house takes a portion of everyone’s money and puts the rest in the pot. Then the house chooses a number all the people who chose that number split the money in the pot. If no one chose the number the pot remains untouched and the game is repeated. This allows the pot to grow arbitrarily large which can make lottery tickets occasionally be worth the price. So, the full strategy is not “not to play” but “not to play until the numbers get big enough.” (Which, as you will see below, is essentially never.)
In general, a lower-bound on the expected payout (assuming I calculated correctly) is ((p+t c)/n)/(n/t) = (p t + c t^2)/(n^2) where p is the starting pot, n is the number of numbers that can be drawn (choosing 3 numbers from 0..99 in order would have n=100*100*100=1,000,000), t number of tickets sold and c is the amount added to the pot for each ticket. For example, the Ohio megamillions game (ignoring the fixed prizes) has n=258890850. They don’t state c, but we can estimate it is larger than 1/3. So, you can make a slight profit when p > (201073416641167500 – t^2)/(3 t). If we assume that 20 million tickets are sold for each drawing at $1 per ticket, you make a profit on average at a jackpot of about $3,344,556,944. Of course, the variance is so high, you’ll never see that very small profit in your lifetime. (If the jackpot were that big every time and you played 2x/week 50 weeks/yr for 50 years 0.002% chance (1 in 50,000) of winning.)
In all, don’t bother. If you need the excitement, invest $1/day in an index fund. Then listen to the daily stock report. If the S&P 500 went up, you win (yay!), and if it went down, you lost (cry). And after 50 years, you’ll probably have at least twice the $18,000 you put into it (even after subtracting taxes and inflation)
I’ve heard similar arguments about probability and intelligent design. Not to step on religious toes, but can the “probability of life being formed is equal to a 747 being made from a twister” be “thrown out” with the same logic as the dice roll?
Love Life and Prosper
@Locutus
First, how the earliest life forms formed is still a very open topic. “We don’t know, but we’re working on it so be cool for, like, five minutes” is a totally valid answer in every science. Second, “life” itself is very difficult to define. The simplest self-replicating structures don’t need to be particularly sophisticated (by aeronautical standards).
But no, this dice thing doesn’t apply.
I don’t agree with the statement, “The only way to win is not to play.” I buy a lottery ticket once in a while. I fully understand the odds, I can afford to lose the money and understand I probably will. On the other hand, I also know that someone is definitely going to win, and if I don’t play, it definitely won’t be me. Buying 1 ticket multiplies my odds of winning the jackpot *infinitely*, from 0, to 1 in 12 million; buying a second ticket only doubles my chances at most, so I only ever by 1.
@Scott
Without buying a ticket, you can still win. Someone else can buy you a winning ticket. You can find a winning ticket on the sidewalk. You might say: those are incredibly unlikely events; but so is winning. So, your expected value from not buying a ticket is actually positive whereas your expected value from buying a ticket is negative.
@Eric
I’m not denying you can win without buying a ticket, I’m simply refuting the statement, “The only way to win is not to play.”
The expected value from buying a ticket is only negative when you measure the value in terms of monetary returns (and you don’t win more than you paid). Using your reasoning, there is no point in buying a theatre ticket, because its value to you is negative in monetary terms. But – like a theatre ticket – part of the value for me is the entertainment factor. Also, if nobody buys a ticket, then there is no jackpot to win, so one could also take the enjoyment of seeing it as their small part towards somebody else’s fortune.
If the payout is less than the odds of winning times the cost of a ticket, all money spent buying tickets is wasted.
Example: tickets are a dollar each, half the money spent on tickets goes in the pot, and the odds of winning are 1 in 10 million.
To win, $10 million must be spent, and $5 million is the prize. Is that REALLY a win? If you believe it is a win, I would like to sell you all my $10 bills for the bargain prize of $20 apiece. I have as many as you want to buy, but there is a minimum purchase of 1000 units. Please let me know if you would like to cash in on this excellent deal.
I am quite comfortable saying ‘You give me the money you spend on a ticket and I will pay out if your numbers come up’. I am more likely to die in my car on the way to work than I am at having to pay out.
Really informative article post. Really thank you! Really Great. best cricket betting app