Physicist: This famous equation is a little more subtle than it appears. It does provide a relationship between energy and matter, but importantly it does not say that they’re equivalent.
First, it’s worth considering what energy actually is. Rather than being an actual “thing” in the universe, energy is best thought of as an abstract (there’s no such thing as pure energy). Energy takes a heck of a lot of forms: kinetic, chemical, electrical, heat, mechanical, light, sound, nuclear, etc. Each different form has it’s own equation(s). For example, the energy stored in a (not overly) stretched or compressed spring is 
The useful thing about energy, and the only reason anyone ever even bothered to name it, is that energy is conserved. If you sum up all of the various kinds of energy one moment, then if you check back sometime later you’ll find that you’ll get the same sum. The individual terms may get bigger and smaller, but the total stays the same.
For example, the equation used to describe the energy of a swinging the pendulum is 
In fact, it isn’t obvious that all of these different forms of energy are related at all. Joule had to do all kinds of goofy experiments to demonstrate that, for example, the sum of gravitational potential energy and thermal energy stays constant. He had to build a machine that turned the energy of an elevated weight into heat, and then was careful to keep track of exactly how much of the first form of energy was lost and how much of the second was gained.
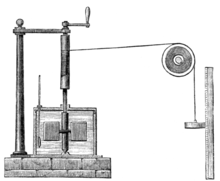
As the weight falls, it turns an agitator that heats the water. Joule’s device couples the gravitational potential of the weight with the thermal energy of the water in a tank. The sum of the two stayed constant.
Enter Einstein. He did a few fancy things in 1905, including figuring out a better way of doing mechanics. Newtonian mechanics had some subtle inconsistencies that modern (1900 modern) science was just beginning to notice. Special relativity helped fixed the heck out of that. Among his other predictions, Einstein suggested (with some solid, consistent-with-experiment, reasoning) that the kinetic energy of a moving object should be 
Up to about 40% of light speed (mach 350,000), 
So, that was Einstein’s contribution. Before Einstein, the kinetic energy of a completely stationary rock and a missing rock was the same (zero). After Einstein, the kinetic energy of a stationary rock and a missing rock were extremely different (by mc2 in fact). What this means in terms of energy (which is just the sum of a bunch of different terms that always stays the same) is that “removing an object” now violates the conservation of energy. E=mc2 is very non-specific and at the time it was written: not super helpful. It merely implies that if matter were to disappear, you’d need a certain amount of some other kind of energy to take its place (wound springs, books higher on shelves, warmer tea, some other kind); and in order for new matter to appear, a prescribed amount of energy must also disappear. Not in any profound way, but in a “when the pendulum swings up, it also slows down” sort of way. Einstein also didn’t suggest any method for matter to appear or disappear (that came later). So, energy is a sort of strict economy (total never changes) with many different currencies (types of energy). Einstein showed that matter needed to be included in that “economy”, and that some things in physics are simpler if it is.
While it is true that the amount of mass in a nuclear weapon decreases during detonation, that’s also true of every explosive. For that mater, it’s true of everything that releases energy in any form. When you drain a battery it literally weighs a little less because of the loss of chemical energy. The total difference for a good D-battery is about 0.015 picograms, which is tough to notice especially when the battery is ten billion times more massive. About the only folks who regularly worry about the fact that energy and matter can be sometimes be exchanged are high-energy physicists.
Cloud chamber tracks like these provided some of the earliest evidence of particle creation and have entertained aged nerds for decades.
As far as a particle physicist is concerned, particles don’t have masses; they have equivalent energies. If you happen to corner one at a party (it’s not hard, because they’re meek), ask them the mass of an electron. They’ll probably say “0.5 mega-electronvolts” which is a unit of energy (the kinetic energy of a single unit of charge accelerated by 500,000 volts). In particle physics, the amount of energy released/sequestered when a particle is annihilated/created is typically more important that the amount that a particle physically weighs (I mean, how hard is it to pick up a particle?). So when particle physicists talk shop, they use energy rather than matter. For those of us unbothered by creation and annihilation, the fact that rest-mass is a term included among many different energy terms is pretty unimportant. Nothing we do or experience day-to-day is affected by the fact that rest-mass has energy. Sure the energy is there, but changing it, getting access to it, or doing anything useful with it is difficult.
The cloud chamber picture is from here, and there’s a video of one in action here.
Super well written! At least, I found it far more informative and entertaining than I thought the question could allow.
You write: “About the only folks who regularly worry about the fact that energy and matter can be sometimes be exchanged are high-energy physicists.”
Does this mean we should think of E=mc^2 as related or belonging together with these so-called “symmetry breakings” that notoriously differentiated forms of physical forces when the Universe cooled below a corresponding threshold temperature some short while after the Big Bang?
If someone presented me with a narrative according to which “inflation” is a time after the Big Bang whence E=mc^2 is fully realized while its manifestations today are like remnants, secondary effects, how would this be misleading?
I would not have called E the Kinetic Energy. To my mind, Kinetic Energy would be (MC^2)/(1-(v/c)^2)^.5 – MC^2, so it goes to zero at V=0, and the residual is Rest Mass Energy. Your E then is the total energy.
Boris, current cosmology suggest that energy and matter were freely converting back and forth under E=MC^2 throughout the inflationary period, and until the temperature dropped enough that there was no longer enough energy floating around to easily create particle pairs.
The interesting asymmetry is related to why we did not end up with exactly the same amount of matter as anti-matter.
Matter is an illusion of energy. As our physical bodies are also part of the illusion, we can’t see it for what it is. Like an optical illusion, the thing (in this case matter) isn’t there, we just assume it’s there and are so accustomed to and immersed in the illusion that we are unable to see it.
Einstein derived the E=mc^2 rule from special relativity and the simple conservation of mass /energy laws, so you don’t need to understand general relativity to follow Einstein’s argument: Any high school student with an understanding of algebra, simple physics (conservation of energy, conservation of mass) , and the special theory of relativity should be able to follow his argument to its logical conclusion.
from project gutenberg
http://www.gutenberg.org/ebooks/5001
“The principle of relativity requires that the law of the concervation
of energy should hold not only with reference to a co-ordinate system
K, but also with respect to every co-ordinate system K1 which is in a
state of uniform motion of translation relative to K, or, briefly,
relative to every ” Galileian ” system of co-ordinates. In contrast to
classical mechanics; the Lorentz transformation is the deciding factor
in the transition from one such system to another.
By means of comparatively simple considerations we are led to draw the
following conclusion from these premises, in conjunction with the
fundamental equations of the electrodynamics of Maxwell: A body moving
with the velocity v, which absorbs * an amount of energy E[0] in
the form of radiation without suffering an alteration in velocity in
the process, has, as a consequence, its energy increased by an amount
E[0]/{sqrt(1 – (vv/cc)}”
i’ve wondered whether this allows light to spontaneously become matter (neutral mesons most likely)…
because if it does… suppose you had a powerful laser on the front of a spaceship that has accelerated ludicrously close to the speed of light, and turns on the laser. to some passing observer in a relative rest frame, the photons could be doppler-blueshifted to such an extent that their energy is sufficient for matter to form. in that case, what does that mean for the photons from the spaceship’s frame of reference?
Matter creation is generally pair production, and those matter / anti-matter pairs could be just about anything energetically possible.
Quantum mechanically, you can even produce them without available energy, generally described as virtual particles.
My quick intuition is that the observer would see blue-shifted photons but at a much lower density (clock slow on the ship so photon emission rate slowed & different apparent spacial densities), so both would end up with consistent measurements.
@Cryptographer
hence the laser requirement – the photons are not being emitted one at a time, many would be emitted in phase and in groups. may not be the best example but my point remains:
if you have two photons who interact in one frame of reference and create matter, there will always be a receding frame of reference where the energy was not sufficient. counter-intuitively the matter would appear to be more massive due to recession velocity, with less energetic photons going in (from the receding frame of reference). i have no idea how to reconcile this situation because it is unavoidable so long as photons can interact to create matter under some circumstance.
after much re-reading, i think what i’ve stumbled on is a variant of the unruh effect (and if not it is still a fascinating read). that boils down to the fact that an accelerating observer would see a vacuum (non-empty, just lowest state) with different energy than an inertial / stationary observer.
can’t find much info on it though… is there any intuitive approach that explains why you would (if the theory is correct) observe vacuum blackbody radiation while in an accelerating frame only?
Your explanation incorrectly conflates mass-energy equivalence in general with the rest mass-energy of fundamental particles (that being only one example), and also suggests falsely that this was Einstein’s original discovery. You can see this is not correct by noting that while it is true that mass decreases when a battery loses chemical energy, no fundamental particles are destroyed in the process.
What E=mc^2 means is that mass is a measure of the energy content of a body, not an additional form that enters into a conservation equation. To state it simply, when a body loses energy E, its mass decreases by E/c^2. In the chemical energy example, there is a definite amount of chemical energy stored in the battery which is lost as these chemicals react to produce electricity. In this process energy is conserved in the simple sense: the electrical energy gained is equal to the chemical energy lost. Since mass is a measure of energy content of a body, the battery with less chemical energy now has a smaller mass. Nowhere does the {delta}mc^2 energy (corresponding to the smaller rest mass) enter into the conservation equation. Nor are any particles created or destroyed. The battery has exactly the same number of electrons, protons, and neutrons as before, they are simply re-arranged. This shows that: (i) mass cannot be considered an additional form of energy along with kinetic and potential energies, and (ii) E=mc^2 is a general law that does not specifically concern the creation and destruction of particles.
Einstein’s statement of E=mc^2 did not have to await the discovery of antimatter to have relevance. In his original paper, he uses an example of a body at rest emitting light with energy E, and shows that relativity demands that the mass of the body decrease by E/c^2. There is no mention of energy changes associated with matter appearing or disappearing.
Now, it so happens that matter/anti-matter can be created or destroyed and in these processes it is useful to think of mc^2 energy in the way you describe. Based on the original interpretation though, the implication is that the rest mass of a particle is not a sort of “frozen” energy, but a measure of some other other interaction associated with the existence of the particle. In modern quantum field theories, certain particles gain mass by interacting with the Higgs field (of the now famous Higgs Boson). The idea is that the electron for example, should be massless, but effectively acts massive due the energy of the Higgs interaction.
So indeed the meaning of E=mc^2 is subtle, and I feel the general conclusion should be that it means mass is measure, rather than a form, of energy.
So in short what is the 2 or 4 words explain this e=mc² energy mass speed of time?
The question can be answered in three words – we don’t know. To that one might add, we may know in fifty years.
The concept of not yet knowing something is crucial to physics. If one doesn’t admit that a question is unanswered, the chances of finding an answer for it go way, way down. People like Einstein and Newton were prepared to admit the gaps in our knowledge. So they left room for new ideas.
In modern physics, a good physicist will do the same, while a bad one will say or imply ‘that’s just the way it is’, when they should say ‘we don’t know, but we may know in fifty years’. Bad physicists just can’t conceive of the idea that there is physics out there we don’t yet know about.
can someone that understands this well email me I would love to learn more.
– bluesbumcharlie@gmail.com
I was told recently by a scientist that kinetic énergy was the product of the motion of mass. That kinétic énergy didn’t produce the motion of the mass as I thought.
So I asked him what kind of energy was responsible for the translation from “rest-mass” to “mass in motion”. I didn’t get any answer.
As for energy being “abstract”. If I refer to the Big bang, witch occured at 10^-43 sec after time zéro, because a volume of any kind couldn’t appear before thatb (Planck’s lenght), the “explosion” was one of space-time and not of matter (matter came in the universe some time after that “explosion”).
And since the Big bang was a manifestation of “motion” in all directions creating à volume of space-time, I fell that the Big bang could be the result of a “release” of kinetic energy that accumulated during Planck’s era. Simple spéculation based on logic, of course.
OK my teacher said that for it to be correct(meaning E=mc2) e has to go up and so does m but c2 stays the same.plzzz help i dont get it.thx for any help 🙂
We also have hv or hf as hv=E=mc^2
This is for electromagnetic radiation.
h is Planck’s constant; and v or f is the frequency of the radiation.
hv, therefor, equals mc^2.
hv=mc^2
I want to know about
1) does all the matter have the energy when there are in rest? ( 1kg wood and 1kg iron has same energy )
2) Can we say by the equation (E=mc^2) Eisenstein say that mass can’t travel more then light’s velocity ?.
3) this isn’t directly related but some what related , what is the speed that we need to travel if we need to go back to the past and future ?
I nitpick your language. E=MC2 does NOT say the two are the same thing. I agree with that. But instead of “same thing” you chose the word “equivalent”, I think that’s EXACTLY what Einstein is saying. Since one can be changed into the other in a definite predictable way we can say they are equivalent. (Like Einstein’s great principle of General Relativity: Gravity and acceleration can be treated as the same thing. And, he calls it his equivalence principle. In fact he is quoted as once saying that he wished the word “relativity” had never been used. Instead he wanted it to be equivalence or unchanging things. Observers cannot agree about the speed of an object (it’s relative), but they CAN agree about the length of the space time vector being the same for all observers.
Thank goodness though that you didn’t say that because the formula included the speed of light that explains why we get SO MUCH energy out of a tiny mass. The problem being that “so much” and “tiny” are arbitrary adjectives with no scientific meaning at all (largER has meaning, largEST does not).
Anyway, it’s trivial to create a new SI that defines the speed of light as 1 putting the formula in a much more intuitive form: E=C (though you need to control the dimensions of the result).
E=MC2 stands for energy , mass, and what?
@Cindy Lu
C is the speed of light.
c must be a very large number, but in popular use (layman) it is always expressed as a ratio: distance / time. If time & space are different things it would seem this ratio can never be a number that can properly be squared and multiply m. [x apples per y oranges.] Before it can be a “top heavy fraction” an equivalence must be known, yes?
So is it correct e=mc^2 incorporates equivalence of time & space? Can it be expressed as one number, or why not?
Must thank JT Rubin for great contribution to understanding with original ‘splain.
I mean can c be expressed as one number (if any doubt).
C is a speed, so it’s always expressed as a ratio of distance traveled to the time it takes to travel that distance. You can tell that both the distance and time are necessary, because if you try to change either or both, then the value of c changes. For example, in meters and seconds c=2.99×10^8m/s. In furlongs and fortnights c=1.80×10^12Fur/For.
@The Physicist
Sorry. Thought I was clear I know it’s a ratio. That is cause of my question, not answer. If my question opaque, I try this way:
Speed is a ratio and value but not a number. To treat it as “fraction” would ignore that the numerator and denominator are values for different things. Or are they? That was my ultimate question.
Maybe you can “divide” number of meters by number of seconds and get a number, but how does that make any sense? Note, if distance in miles, result is different! This is not changed if mass is multiplied by distance, result divided by time.
So I considered if the formula is not for computation at all but only expresses a *relationship*, as any ratio does. This seems unsatisfactory as I have read of accepted verifying experiments in which the units of energy (joules) are measured and the result is “correct”. But if the joules are a number, so must be the right side. No?
E = mc^2 :
m : mass, in kilograms (kg) = 1 kg or ( 1 x 10^0 kg)
c^2 : velocity of light (squared), in meters per second (m/s) = ( 9 x 10^16 m/s)
E : Energy, in joules (J) = ( 9 x 10^16 J)
m x c^2 = E
m ( 1 x 10^0 kg) x c^2 ( 9 x 10^16 m/s) = E ( 9 x 10^16 J)
NOTE: 1 kg of matter = ( 9 x 10^16 J) of energy
ALL matter is made of atoms that contain “nucleons” , term for protons and neutrons
Each nucleon contains ( 1.5 x 10^-10 J) of energy
ALL matter is the same in terms of the number of nucleons per kg,
and a 1 kg mass of ANY matter consists of ( 6 x 10^26 nucleons)
All the energy in 1 kg of matter:
( 6 x 10^26 nucleons) x ( 1.5 x 10^-10 J) = ( 9 x 10^16 J)
NOTE: 1 kg of matter = ( 9 x 10^16 J) of energy
A smaller version, where 1 gram (g) = 0.001 kg ( 1,000 g per kg):
1 g of matter has ( 6 x 10^23 nucleons) x ( 1.5 x 10^-10 J) = ( 9 x 10^13 J) <<
E = mc^2: m ( 1 x 10^−3 kg ) x c^2 ( 9 x 10^16 m/s ) = E ( 9 x 10^13 J) <> Fission: splitting a heavier atom ( 92 Pu-239 ) into two lighter atoms
( 54 Xe-134 and 40 Zr-103).
>> Fusion: binding two lighter atoms ( Tritium and Deuterium ) into a heavier atom
( Helium).