Physicist: A nearly equivalent question might be “how can you prove freaking anything?”.
In empirical science (science involving tests and whatnot) things are never “proven”. Instead of asking “is this true?” or “can I prove this?” a scientist will often ask the substantially more awkward question “what is the chance that this could happen accidentally?”. Where you draw the line between a positive result (“that’s not an accident”) and a negative result (“that could totally happen by chance”) is completely arbitrary. There are standards for certainty, but they’re arbitrary (although generally reasonable) standards. The most common way to talk about a test’s certainty is “sigma” (pedantically known as a “standard deviation“), as in “this test shows the result to 3 sigmas”. You have to do the same test over and over to be able to talk about “sigmas” and “certainties” and whatnot. The ability to use statistics is a big part of why repeatable experiments are important.
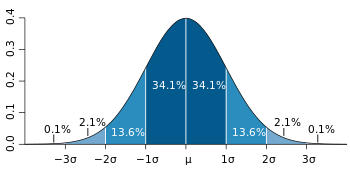
When you repeat experiments you find that their aggregate tends to look like a “bell curve” pretty quick. This is due to the “central limit theorem” which (while tricky to prove) totally works.
“1 sigma” refers to about 68% certainty, or that there’s about a 32% chance of the given result (or something more unlikely) happening by chance. 2 sigma certainty is ~95% certainty (meaning ~5% chance of the result being accidental) and 3 sigmas, the most standard standard, means ~99.7% certainty (~0.3% probability of the result being random chance). When you’re using, say, a 2 sigma standard it means that there’s a 1 in 20 chance that the results you’re seeing are a false positive. That doesn’t sound terrible, but if you’re doing a lot of experiments it becomes a serious issue.
The more data you have, the more precise the experiment will be. Random noise can look like a signal, but eventually it’ll be revealed to be random. In medicine (for example) your data points are typically “noisy” or want to be paid or want to be given useful treatments or don’t want to be guinea pigs or whatever, so it’s often difficult to get better than a couple sigma certainty. In physics we have more data than we know what to do with. Experiments at CERN have shown that the Higgs boson exists (or more precisely, a particle has been found with the properties previously predicted for the Higgs) with 7 sigma certainty (~99.999999999%). That’s excessive. A medical study involving every human on Earth can not have results that clean.
So, here’s an actual answer. Ignoring the details about dice and replacing them with a “you win / I win” game makes this question much easier (and also speaks to the fairness of the game at the same time). If you play a game with another person and either of you wins, there’s no way to tell if it was fair. If you play N games, then (for a fair game) a sigma corresponds to excess wins or losses away from the average. For example, if you play 100 games, then
1 sigma: ~68% chance of winning between 45 and 55 games (that’s 50±5)
2 sigma: ~95% chance of winning between 40 and 60 games (that’s 50±10)
If you play 100 games with someone, and they win 70 of them, then you can feel fairly certain (4 sigmas) that something untoward is going down because there’s only a 0.0078% chance of being that far from the mean (half that if you’re only concerned with losing). The more games you play (the more data you gather), the less likely it is that you’ll drift away from the mean. After 10,000 games, 1 sigma is 50 games; so there’s a 95% chance of winning between 4,900 and 5,100 games (which is a pretty small window).
Keep in mind, before you start cracking kneecaps, that 1 in 20 people will see a 2 sigma result (that is, 1 in every N folk will see something with a probability of about 1 in N). Sure it’s unlikely, but that’s probably why you’d notice it. So when doing a test make sure you establish when the test starts and stops ahead of time.







We could talk about dice or coins.
We expect a +/- 3.5 sd fluctuation on a fair device.
We should determine if we positive play or we just take past data because we don’t want to fool ourselves.
Example: you and your friend have played 100 times on a coin. 65/35 favoured tails. Tails reached +3sd. You give me this sample. I scan it and find this event. I had 2 choices to find a fluctuation, heads or tails. This same fact means different theories for you and me.
I would not be confident of this +3sd(0.3%) as you would be.
I decide to make a new 100 test.
Tails 55, heads 45. +1sd. So, a 32% event again to tails.
I am not satisfy, lets make a bigger test. 1000. Tails 532(+2sd), heads 468.
So, in what condition we are now?
We tested +1sd in 100 and +2sd in 1000 for tails.
A)What is the chance of this event to be random?
B)how do we get more confidence adding a new +1sd on 1000 test for tails?
C)could we use the first sample (65 tails, 35 heads), the one we consider past results, to take is as a prior probability to use Bayes rules?
Best regards
once if you know the the correct feel and hand weight . twice if you are an amateur. The “loaded” dice will roll to the left or right after a supposed dead stop.
Well, I think there are some things that are certain, i.e., proved:
Normal healthy humans have two arms and two legs. Certainty: 100%. Proved!
The Sun is larger than the Moon. You don’t have to measure it 100 times to tell.
Evolution is fact.
There are no unicorns serving in Congress.
Matter is made of atoms.
Time slows down when things move faster. More precisely, a clock on a platform traveling by will appear to move more slowly than one you are holding. OK, maybe this is a 1000 sigma determination. I wouldn’t bet against it!
Gravity exists. As Richard Dawkins says, and I’m paraphrasing from memory here, ~”anyone who doesn’t believe in gravity is invited to jump out of a 10th-story window.~”
Evolution is certainly not a fact. Nice try though.
Since the game has only been played once then how can you tell.
Science has to do with repeatable observations
Cynthia Wiley – Guess you didn’t read the article
Stephen Simpson – “Evolution is not a fact.”
Isn’t it now?
What is “Evolution”? It is a progression, sometimes biological, sometimes, societal, scientific, political, education, even business, it is the progression by which the subject is given increased opportunity for success. Evolution is not guaranteed to go forward, or even at all under certain circumstances, this is true, evolution is by means a force of necessity, most of the time, necessity takes us forward, on rare occasions not at all or even in reverse, depending on the needs of the subject, but evolution takes time, sometimes there isn’t enough time (sorry dinosaurs) and there are consequences, but the “Fact” remains, evolution is a fact, not a guarantee, but a fact nonetheless.