The original question was: … the formula for kinetic energy is 
Worse, you would think that momentum would go up hand in hand with kinetic energy, when the formulas above instead show the latter going up much faster due to the exponent. This also doesn’t make sense.
I’m sure you can do some math to show why it has to be this way, but can you explain in non-math terms why kinetic energy and momentum behave this way?
Physicist: This is pretty unintuitive. In fact, historically this was a whole thing. Buckets of profoundly smart folk argued and debated about whether velocity (momentum) or velocity squared (energy) was the conserved quantity. Turns out it’s both. The difficulty is first that energy can change forms and second that up until the 20th century lab equipment was terrible (and often home-made).
Force is mass times acceleration: F=ma. If you apply a force over a time you get momentum and if you apply force over a distance you get energy. Acceleration times time is velocity, so it should more-or-less make sense that force times time is momentum: 
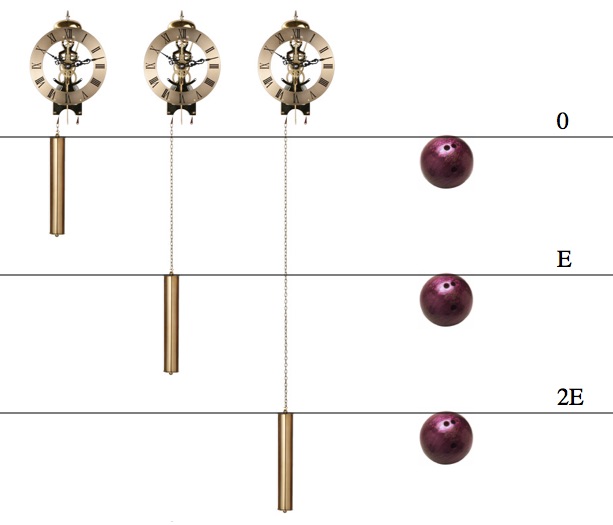
Whether it’s lowered slowly or falling freely, a weight gains the same amount of energy. If it falls twice as far it gains twice the energy.
A decent way to think about force and kinetic energy is to consider a falling weight. Gravity applies a constant force and thus a constant acceleration. If you tie a string to that weight you could power, say, a clock. Every meter it’s lowered it provides the same amount of energy, so lowering it 2 meters provides twice the energy as lowering it 1 meter.
Now imagine the weight free-falling that distance (instead of being slowly lowered). After the first meter it’ll already be moving, so it’ll fall through the second meter faster and in less time. The velocity gained is acceleration times time, so since it spends less time falling through that second meter, the falling weight spends less time accelerating and gains less speed.
But it still has to gain the same amount of energy every meter it falls. Otherwise weight-powered clocks would act really weird (a chain twice as long would yield only √2 as much energy). That means that at higher speeds you gain the same amount of energy from a smaller increase in speed. Or (equivalently) once you’re moving faster, the same increase in speed produces a greater increase in energy. This sometimes seems to produce paradoxes, but doesn’t.
The change in energy is greater for the same change in speed for different starting speeds.
With a little work and some calculus (see the answer gravy below) you can make this a lot more rigorous and you’ll find that the relationship between energy and velocity is exactly 
If it bothers you that energy doesn’t scale proportional to velocity, keep in mind that we’ve got that covered: momentum. Ultimately, both momentum and energy are just names for numbers that can be calculated and for which the total never changes. That which we call momentum by any other name would be as conserved.
Answer Gravy: Energy or work is force times distance: E=FD. When all the variables are constant finding the work done is just a multiplication away. However, when the variables aren’t constant finding the work done requires integration. The question of this post is one of the big reasons behind why calculus was originally invented. If you want to learn intro physics then please, for your own sake, learn intro calculus first. It is so much easier to talk about position, velocity, and acceleration (intro physics) when you can say “acceleration is the derivative of velocity and velocity is the derivative of position”. If you start physics with just a little calculus background, then you and your physics professor will high-five at least twice daily. Guaranteed.
Instead of a single distance with a constant force, we chop up the distance into lots of tiny pieces dx long and add them up. So a better, more universally applicable way of writing “E=FD” is 
What we’ll calculate is the energy gained by an object that starts at rest, is pushed by a force F(x) over a distance D, and moves from position x=0 at time t=0 to position x=D at time t=T.
![\begin{array}{ll} E=\int_0^D F(x)\,dx \\[2mm] =m\int_0^D a(x)\,dx & \textrm{(F=ma)}\\[2mm] =m\int_0^T a(t)\frac{dx}{dt}\,dt & \textrm{("Variable substitution". Chain rule for integrals.)}\\[2mm] =m\int_0^T a(t)v(t)\,dt & \textrm{(Velocity is the time derivative of position.)}\\[2mm] =m\int_0^T \frac{dv(t)}{dt}v(t)\,dt & \textrm{(Acceleration is the time derivative of velocity.)}\\[2mm] =m\int_0^T \frac{d}{dt}\left[\frac{1}{2}(v(t))^2\right]\,dt & \textrm{(Chain rule for dervatives.)}\\[2mm] =m\left[\frac{1}{2}(v(T))^2-\frac{1}{2}(v(0))^2\right] & \textrm{(Fundamental theorem of calculus.)}\\[2mm] \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D++E%3D%5Cint_0%5ED+F%28x%29%5C%2Cdx+%5C%5C%5B2mm%5D++%3Dm%5Cint_0%5ED+a%28x%29%5C%2Cdx+%26+%5Ctextrm%7B%28F%3Dma%29%7D%5C%5C%5B2mm%5D++%3Dm%5Cint_0%5ET+a%28t%29%5Cfrac%7Bdx%7D%7Bdt%7D%5C%2Cdt+%26+%5Ctextrm%7B%28%22Variable+substitution%22.+Chain+rule+for+integrals.%29%7D%5C%5C%5B2mm%5D++%3Dm%5Cint_0%5ET+a%28t%29v%28t%29%5C%2Cdt+%26+%5Ctextrm%7B%28Velocity+is+the+time+derivative+of+position.%29%7D%5C%5C%5B2mm%5D++%3Dm%5Cint_0%5ET+%5Cfrac%7Bdv%28t%29%7D%7Bdt%7Dv%28t%29%5C%2Cdt+%26+%5Ctextrm%7B%28Acceleration+is+the+time+derivative+of+velocity.%29%7D%5C%5C%5B2mm%5D++%3Dm%5Cint_0%5ET+%5Cfrac%7Bd%7D%7Bdt%7D%5Cleft%5B%5Cfrac%7B1%7D%7B2%7D%28v%28t%29%29%5E2%5Cright%5D%5C%2Cdt+%26+%5Ctextrm%7B%28Chain+rule+for+dervatives.%29%7D%5C%5C%5B2mm%5D++%3Dm%5Cleft%5B%5Cfrac%7B1%7D%7B2%7D%28v%28T%29%29%5E2-%5Cfrac%7B1%7D%7B2%7D%28v%280%29%29%5E2%5Cright%5D+%26+%5Ctextrm%7B%28Fundamental+theorem+of+calculus.%29%7D%5C%5C%5B2mm%5D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{ll} E=\int_0^D F(x)\,dx \\[2mm] =m\int_0^D a(x)\,dx & \textrm{(F=ma)}\\[2mm] =m\int_0^T a(t)\frac{dx}{dt}\,dt & \textrm{(\"Variable substitution\". Chain rule for integrals.)}\\[2mm] =m\int_0^T a(t)v(t)\,dt & \textrm{(Velocity is the time derivative of position.)}\\[2mm] =m\int_0^T \frac{dv(t)}{dt}v(t)\,dt & \textrm{(Acceleration is the time derivative of velocity.)}\\[2mm] =m\int_0^T \frac{d}{dt}\left[\frac{1}{2}(v(t))^2\right]\,dt & \textrm{(Chain rule for dervatives.)}\\[2mm] =m\left[\frac{1}{2}(v(T))^2-\frac{1}{2}(v(0))^2\right] & \textrm{(Fundamental theorem of calculus.)}\\[2mm] \end{array}")
When we say the object started “at rest” we mean “v(0)=0”. Whatever v(T) is, it’s the velocity of the object when we’re done. So, the energy gained by an object that starts at rest and is pushed up to some speed v is
Huzzah for calculus!
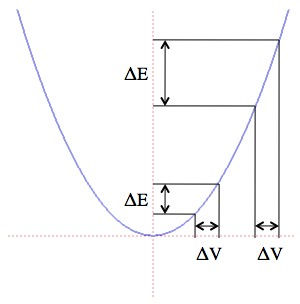
The explanations for the kinetic energy formula sound pretty good. However, in a science such as physics, you need more. The scientific method sets aside personal bias and in its place, it requires that a prediction be tested. This has never been competently done for the kinetic energy formula, or for work (force x distance) for that matter. If you are going test these ideas using the scientific method, you cannot drop something from a height and say, “hey, the work done to an object is equal to the change in the kinetic energy of the object and so we are good.” Why? Well, there are two reasons. The first is that this experiment begins by assuming that work is a valid scientific idea. It is an assumption easily countered (see workenergytheorem.com). More importantly, if the idea of kinetic energy and energy in general are to have any meaning, you have convert chemical or electrical energy into kinetic AND THEN see if the kinetic energy formula is valid. Unfortunately, the kinetic energy formula, or some version of it, has been around since Newton and so, no one believes it possible that this simple formula is wrong. Oh by the way, Newton would argue against the current kinetic energy formula (a fact easily verified via today’s internet). If you want to know with absolute certainty, not just go with whatever everyone else believes, visit my website (workenergytheorem.com) where visitors will learn just how work and the kinetic energy formula came to be and a lot more. Remember, there was a time when “everyone knew” the world was flat and another time when the universe was deemed to exist in a static state; these ideas are no longer held because they were overturned by science. And for the record, everything on my website can and should be verified; it does not require anyone to take anything on faith unlike the lessons taught as fact in physics 101.
The calculus proof can be bypassed with simple math just using f=ma, x=(1/2)at^2 in the formula work energy equals force times distance giving
KE = fx = (1/2) m a^2 t^2
Then use v=at gives usual KE = 1/2m v^2
The physicist intuitive explanations are good. Also there are intuitive arguments too requiring speed squared using simple collisions with symmetries , or time invariance, or jumping reference frames.
Also I think we intuitively know from experience in physical world that fast objects really do pack a disproportionate punch. Disproportionate being the key.
In car accidents for example we know crashing into a wall at 100 mph is going to be much worse than simply twice as bad as crashing at 50 mph. At 50 you may break one bone whereas at 100 you would be happy to just break four bones. Each break absorbing equal energy.
I’m sure there are lots more such practical and semi intuitive examples.
A high school, non-calculus, version of an answer is this:
Imagine pushing a mass m with a constant force F through a distance d. By Newton’s second law, the acceleration will be
a = F / m
From kinematics, we have the formula
v^2 = 2ad
Substituting for a:
v^2 = 2 (F / m) d
Rearranging,
Fd = 1/2 m v^2
Larry gives the typical textbook derivation. It uses the formula v^2=2ax which is not very memorable. I think it is neater via the wholly equivalent proof using the basic and famous x= one half “a” times “t” squared.
@Bob Berenz:
The thing that’s wrong with your argument is that they have actually tested this formula before. They have proved this formula is correct (or is it). It has also been proven, altogether with the theories of relativity by Albert Einstein, that the formula only holds true for very low speeds. For speeds lower than 66 000 km/s, it holds true within 0.1% of v, while it holds true for within 1% of v when the speeds are lower than 120 000 km/s. The actual formula is given by Einstein’s equation: KE=mc^2/(sqrt\1-v^2/c^2\)-mc^2, which, as a Taylor series, is expanded into mc^2(v^2/2c^2+3v^4/8c^4+5v^6/16c^6…)=(mc^2)(v^2/2c^2)+(mc^2)(3v^4/8c^4)+(mc^2)(5v^6/16c^6)…, which is approximated simply to (mc^2)(v^2/2c^2) at relativistic low speeds (the other terms are divided by a power of c^2, which makes their value incredibly small unless v is close to c). Reducing (mc^2)(v^2/2c^2) obviously becomes simplified to simply 1/2*mv^2, which only holds true for very low speeds, but it is however, a very goo enough approximation whatsoever.
QUESTION: All, on this subject (focusing on Pabl0 Jeynes answer, stating x = 1/2 a t^2), I am an aeronautical engineer, and I am growing a strong interest in Work & Energy based analysis. I am evaluating all of the KE = 1/2 m V^2, U=1/2 k x^2, u = 1/2 E epsilon^2, and dynamic pressure, p = 1/2 rho v^2, where V, k, E, and rho are all constants (I am loving all of you physics folks). I am now puzzled about x = 1/2 a t^2 (from integrating d^2 x/dt^2 = a). If I substitute (x = 1/2 a t^2) into a PE=mgh, I get a strange looking PE=mg(1/2 g t^2) = 1/2 m (g^2) (t^2). Is this correct? My question is, how does (x = 1/2 a t^2) nicely into an energy equation of the form of KE, U, u, and p up above? It almost looks like x = 1/2 a t^2 by itself is an energy equation, but if W=U=Fx, then W=U=x = 1/2 F a t^2, (using a or g) but then what kind of constant is F times a?
I’m not disputing the principle of kinetic energy, but the example of a clock driven by a falling weight is not helpful. In actual clocks of this kind the descent of the weight is controlled by an escapement mechanism, regulated by a pendulum or balance spring, which only allows the weight to descend in short equal periods of time. In effect, the weight is always moving at an equal speed, so there is no acceleration to be taken into account. The fact that such clocks can keep good time therefore does not prove anything.
@Gregory Kress,
If you have W = 1/2Fat^2, you could use Newton’s second law and write F = ma, and replace to get W = 1/2ma^2t^2. x = 1/2at^2 assumes that you have constant acceleration, so that the acceleration times the time gives the velocity, i.e, v = at. Therefore, v^2 = a^2t^2, and so you can use this to obtain W = 1/2mv^2, which is just the kinetic energy formula. Note that this assumes that you start off at 0 velocity so that the change in kinetic energy is just your final kinetic energy.
Same thing for potential energy. Assuming you start off with 0 potential energy and fall, you get 1/2mg^2t^2, and since v = gt, U = 1/2mv^2, which is just energy conservation.
Interesting comment above about the car crash. What’s worse, crashing into an identical car that’s still (without breaks applied) when you’re travelling 100mph, or having a head on crash with that car when you’re both travelling 50mph? Apart from secondary issues I’d have expected them to be as bad as each other, though there’s twice as much energy in the first crash?
@ Danshyl and all,
Oh, thank you!! You have restored harmony to my world. I was always curios how to relate PE=mgh to KE=1/2mv^2. I didn’t understand why PE was energy, but it didn’t have a 1/2 or a component^2. I guess I always did accept that W=E=Fd, where F=mg and d=h. However, now understand the derivation:
1. a = dv/dt
2. dv = a dt
3. integrated, v = a t
substituted into:
4. v = dx/dt
5. dx=v dt = a t dt
6. integrated, x = 1/2 a t^2
Substituted into Potential Energy, PE = mgh = mgx
7. PE = m g (1/2 a t^2) = m a (1/2 a t^2), where g = a
8. PE = 1/2 m a^2 t^2 = 1/2 m (a t)^2
Substituting in expressions 3 above, v = a t,
9. PE = 1/2 m v^2 = KE
Raise a weight and pin it into place to create PE=mgh. Pull the pin, the weight falls, accelerates, increases velocity, and becomes KE=1/2mv^2. Energy is conserved!! I love it. I probably learned that in Physics in high school, but for got it since I was so concerned that I was going to pass EnglishIV because I hadn’t finished reading Tom Sawyer. However, I am just an engineer, did I break any rules of math or physics in my derivation?
Hey @Andy B , there is indeed twice the energy in the first 100-0 crash, before the crash. After the crash there is still energy as assuming the same size cars one has decelerated from 100 down to 50, while the other gains energy going from 0 to -50. If you do the calcs you find there is still half the energy left in the system so the energy loss is the same, so the damage is the same. That’s why they talk of closing velocity.
I admit, I did have to think about it a bit and fire up the spread sheet!
Stu H
I have other intuitive ideas:
1) a balance, with one plate twice as long as the other, would require twice the weight on the sort plate in order to maintain equilibrium. If the sort end starts moving 1 mm (=L1 *α) downwards, the long end would start moving 2 mm (=L2*α) upwards, in the same span of time. So we can imagine that F*ds is the amount of (constant) energy, and not F*dt.
2)In an euclidean space, an object moving Sx on the x axis, and moving simultaneously Sy on the y axis, would result in moving a total of s=√(Sx²+Sy²), and moving with contant velocity of v= √(Vx²+Vy²)
But imagine that the objet only moved Vx on the x axis at first, being Vy=o then. If you applied a Fy force on the y axis, until the object reach certain Vy on that axis.
To the initial amount of Energy (which was a function of Vx), we have to ADD the amount of the energy gained with the force Fy (which is a function of Vy). So, the addition of E(Vx)+E(Vy) should be equal to the total Energy (which is a function of v), thus being E(v)= E(Vx)+E(Vy), that implies the energy should be a function of square velocity in Euclidean spaces.
@JM Garcia. Totally agree! I had thought similar things using pulley gear ratio, and your second point interestingly connects into Pythagoras into the basis for kinetic energy formula which I noticed before is quite necessary and needs Pythagoras to be dependant on component squares in any number of dimensions which of course is true. So energy conservation sort of forces Pythagoras to use squares and not for example work with cubes in 3D, etc. (Admittedly this is a kind of reverse logic)
Can’t remember how his came my way, but looking back it does occur to me that the original question was looking for a non mathematical, inuitive explanation. There’s an awful lot of maths in the replies!
So imagine you’re car breaks down and you have to push it. First you have to get the thing moving. This takes hardly any energy. You have to push hard you it won’t puff you out. You are not walking or running, just pushing. You get to 1 mph and your are still only moving slowly and mostly just pushing. Now let’s skip a few mph. You get to 5 mph. It’s almost a run. You want to get to 6 mph, just 1 mph more. In order to do this you have to push just as hard as you did to get the thing from 0-1 mph, while running!
That’s a lot more energy you have to expend.
Another way to think of it is in terms of power. Force * velocity. (Sorry, maths). When the car is static there is no power, only force. Until the car actually moves there is no power or energy expended. Every mph added requires more energy to achieve, so for the same power each extra mph take longer to happen.
Regards to all!
Extra energy required for each increase in mph due to extra air resistance from increased speed….also with velocity loss at lower speeds comes a slower velocity loss than velocity loss at higher speeds…trajectory tables show that difference
“Extra energy required for each increase in mph due to extra air resistance from increased speed….also with velocity loss at lower speeds comes a slower velocity loss than velocity loss at higher speeds…trajectory tables show that difference” – Charlie
Space has pretty much no air resistance but yet it takes more energy to increase in speed and another thing Science is used in kph