Physicist: Yes!

Just to be clear, we’re not talking about this. This is cheating.
Mathematicians are pretty good at talking about things in spaces with any number of dimensions. Sometimes that math is fairly easy and even intuitive. For example, a line has 2 sides (ends), a square has 4 sides, a cube has 6 sides, and a hypercube has __* sides.
Ordinary knots (that you can tie with string) can only exist in exactly 3 dimensions. It’s impossible to create a knot in 2D since every knot involves some amount of “over-and-under-ing” and in 2D space there’s none of that. Because it makes the math more robust, mathematicians always talk about knots being tied in closed loops rather than on a bight. In part because once you’ve connected the ends of your string the knot you’ve got is the knot you’ve got, and that invariance is very attractive to math folk.
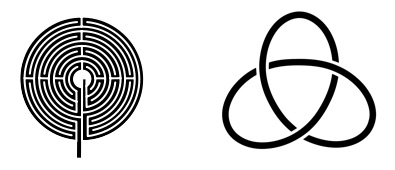
Left: In two dimensions, no matter how complicated and convoluted your string is it can never be tied in a knot. Right: Even the simplest knot requires at least three over-under excursions into three dimensional space to get around self-intersections.
In 2D, if you have a dot inside of a circle, it’s stuck. But if you have access to another dimension (“dimension” basically means “direction”), then you can get the dot out. In exactly the same way, if you can “lift” part of a regular knot into a fourth dimension it’s like opening the loop and you’re free to untie your knot in the same way you’d untangle/untie anything. Afterwards you just “lower” the segment of the string back so that it all sits in 3D and now you’ve just got a loop of unknotted string (very creatively, this is called an “unknot”). So, you’ve managed to untied your knot without worrying about self-intersections and all it took was an extra dimension.
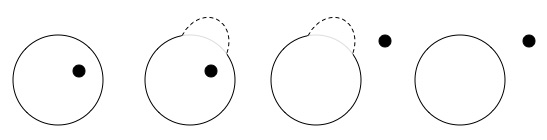
In 2D a dot can be stuck inside of a circle, but if we have the option to “lift” part of the circle in a new direction then the dot can get out. From the perspective of the flat denizens of 2D space, this looks like part of the circle being removed.
All that was just to say: be excited, the way you tie your shoes is only possible in universes similar to (with the same number of dimensions as) our own. You can’t tie a knot in a string in two dimensions and a knotted string in four (or more) isn’t really knotted at all.
The way we talk about ordinary knots is in the context of a loop (tie your knot and then splice the loose ends of the string). The generalization of a loop (a 1-sphere) to higher dimensions is first the surface of a regular sphere (a 2-sphere), then the surface of a hyper-sphere (a 3-sphere) and so on. An N-sphere can be tied in a knot in N+2 dimensional space.
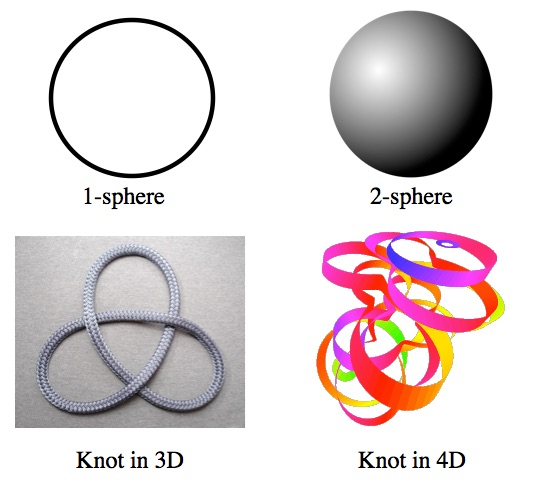
An N-sphere can be tied in knots in N+2 dimensions. 1-spheres can be tied in knots in three dimensions (these are known colloquially as “knots”), which means that they can actually be created. 2-spheres (the surface of a ball) can be tied in knots in four dimensions. The image here is only a cross-section of such a knot.
It turns out that if you have an ordinary knot, you can use it to create a higher dimensional knot. There are a several ways to do this. There’s “suspension“, which usually doesn’t work (the created knot is often not a “manifold“, which is kinda cheating), and there’s also “spinning” which always works.
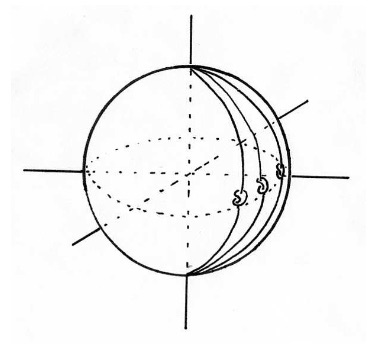
The basic idea behind spun knots.
To create a “spun knot” you rotate it in a higher dimensional space and collect all of the points that it sweeps through. The picture above is more symbolic than applicable. In this picture a knot in 3D is spun to create a sphere that’s still in 3D space, but with a funky-shaped tube running around its equator. That’s not a knot (knot at all). This process needs to be done in four dimensions, where the added direction allows you to get around the self-intersection problem, but the basic idea is the same. So for every knot that you can tie with a loop of rope in 3D, there’s a knot you can tie with a hollow sphere in 4D.
And yes: you can keep going into higher and higher dimensions using the same idea.
While you can’t directly picture a four dimensional knot, you can create cross-sections (the same way a 2-dimensional being might picture 3-dimensional objects using cross-sections). This video (~0.4MB) shows 3D cross-sections of a rotating 4D knot. But be warned: that video is, for lack of a better word, groovy.
Sometimes a group of scientists will get really involved with a particular subject and kinda disappear up their collective butts for a while (especially mathematicians). Eventually one of them will emerge like a prairie dog and bark “fellow dudes and dudesses, we should really send a message to the world so they don’t worry about us” at which point a summarizing paper such as this or this is written (about higher dimensional knots in this case), in an attempt to convey to a slightly broader audience what they’ve been doing.

Mathematicians after a long think.
The tied sheets painting is by Teun Hocks and is from here.
The 4D knot picture and the video are from here.
The spun knot picture was lifted remorselessly from the second paper mentioned earlier.
*8







So how do we tie our shoes in 10 dimensions?
Or to put it another way: what are the implications for string theory ..
It’s a trap!
Number of sides of a hypercube? There would be 16 vertices and 32 edges. How can that represent 8 sides? Is a side to represent a two-sided flat sheet? Confusion reigns! OR, if dimensions represent projections, then each dimension would add 1 two-sided flat sheet….
The study of knots is an interesting application of higher (than three) dimensions. One might wonder if higher dimensions are truly real, or merely a figment of mathematics, if one will pardon the term.
It may also be interesting to recall the history of applying extra dimensions to physics. Basically employing at least one extra dimension (to describe time in SR, special relativity) was first suggested by Hermann Minkowski, Einstein’s former college teacher in mathematics. Extra dimensions worked so well in SR, the cork was pulled, and the genie’s been out of the bottle ever since. We continue to be enthralled by imagining that extra dimensions are not only real, but absolutely necessary. And they are sometimes, at least mathematically, if not intuitively in a heuristic sense.
But originally requiring a 4th dimension for time might be (and might have been) entirely unnecessary. In a way we have already eliminated this by noting any observed dimension is really spacetime. So logically we could say time and dimension appear not only congruent, but essentially the same single property. This brings us back to describing our universe in just 3D spacetime… up, down and sideways (xyz).
As an example, suppose one had a pocketwatch that (in uniform motion) ran at exactly the same rate as Big Ben. One might stand directly below Big Ben and set this pocketwatch to exactly the same time as Big Ben. Then one might proceed to hike out into the countryside, stop and look back. With incredibly accurate attention to detail, one would find that distant Big Ben now reads ever so slightly slower than the nearby pocketwatch. We might assume this “historical view” to be due to the “speed of light” delaying our Big Ben view over the increased distance.
But the dilema comes when we ALSO notice Big Ben also appears smaller (in the x, y axis) than it did before (Actually inversely-proportional-to-the-square-of-the-distance, smaller). Of course it does… we all observe the same. And off-hand, this might be assumed to be very ordinary “relative size”, merely the illusionary result of the architectural vanishing point.
The architectural vanishing point is normally thought of as a non-contender in “real” relativity. But now how do we know the spacetime dimension (z) between us and Big Ben is a linear dimension, if the others (x,y) appear not? How can we measure any z axis exclusively relative to ourselves? Perhaps the z dimension also steadily decreases inversely-proportional-to-the-square-of-the-distance. That would imply a permanent acceleration. And, in principle, an acceleration seems in agreement beyond special relativity. Perhaps we could call it gravity. Or the inevitable curvature of spacetime.
If this were to be so, we could put the genie back in the bottle. Frankly, the geometry of 3D has always been easier to work with, maybe less fun perhaps.
Wes
So how would a sphere look in 4d? I understand a tesseract is the 3d shadow of a 4d cube is it not? But how would a shadow of a 4d sphere look?
A 4d sphere was create a 3d sphere as a shadow.
Imagine a 3d sphere going though a line. And now a 2d circle. They go though the same (a line segment of length=0 to length=diameter of circle/sphere and then back to length=0). And a 3d sphere going though a 2d plane makes a circle that goes from r=0 to r=(r of sphere) and then back to zero. The same would happen as a 4d sphere goes through a 3d environment.
You can actually graph this.
If, you look at the super sub-atomic, the sub-atomic, the atomic, the molecular, the chemical, and the biological you should come to the conclusion that each is a reflection of its predecessor ! That being stated, if you observe heat action w/in our earth’s core, you would observe that same heat energy ebbs, flows, & returns to the core ! So, as to your question, the answer is of course !!! P.S. I hope this explanation isn’t to overly simplified but, alas I am only a ley genius !!!
Why it is always the physicist who write the articles? We need more articles from the mathematican!
Elizabeth: A side is one dimension lower than the object, ie. a hypercube as 8 sides, which are three-dimensional, ie cubes.
I would say probably in quantum realm 2d can have knots. Since we might be a hologram and we have knots, how would that otherwise work?