Physicist: Focus on the one with the highest interest rate. Get rid of it first, completely, before moving on to the next. Debt is a like spiders. If you can only kill a few at a time, kill the ones that are carrying the most eggs. That way: fewer spiders later.
Left: A dollar with a low-interest rate. Right: A dollar with a high-interest rate.
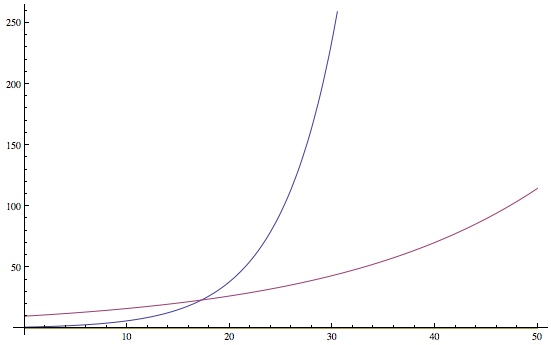
When some faceless corporation is holding your debt they generally give you two numbers: the Principal, the amount you presently owe, and the Interest, the percentage that the principal increases. Rather than just “charging rent” to loan you money, creditors do something infinitely worse: interest means your debt grows exponentially fast.
APR (annual percentage rate) is a common way to express Interest. APR is how much your debt grows every year. For example, if you owe 100 dollars ($/€/£/¥/₮/whatever) with an APR of 15%, then after a year you’ll suddenly owe 
Having debt in a few different accounts makes the situation seem more complicated, but it really isn’t. Each individual dollar increases on its own; the fact that they’re grouped in a given way doesn’t change that. If you’ve got ten buckets full of spiders, your problem isn’t having too many buckets.
The high-interest dollars are the most dangerous, not only because they make new debt-dollars, but because those new dollars have the same new-debt-creating interest rate.
Blue: $1 initially with 20% APR. Reddish: 10$ initially with 5% APR.
Even if you have a lot of Principal in a low Interest account and a little Principal in a high Interest account, get rid of the high interest stuff first. Each of those dollars will turn into more dollars sooner. Exponential functions get out of hand really fast, so the thing to worry about is the Interest Rate: bigger is much, much worse.
Although Interest is the standard way that debt is handled today, it is in no way fair. Creditors are duplicitous folk who, by and large, have the law on their side. After all, they can afford it. So double-check all of the fine print and make sure you know exactly what it says. Your debt is how they make money, so creditors don’t want you to pay all of it off. They genuinely want you to pay the absolute minimum every month and to slip up, just so they have an excuse. Your low-interest loan may not stay low-interest; credit/loan companies have come up with far more ways to trick you into a high-interest program than can be listed here.
So keep an eye on it (that is to say, don’t trust them to do it), make at least the minimum payments (don’t give them an excuse) and pay down the high-interest stuff first, as fast as you can. Every extra dollar you pay toward getting rid of the Principle in a, say, 20% interest account, is equivalent to a 20% investment (which is really good).
An accurate and thought provoking comparison. As someone who lives in Australia I wish I could convert my spiders into debt, it would be much easier to deal with.
Scraping the bottom of the barrel with the questions here. I think most of us come here to expand our knowledge, and not see basic math problems.
What have you got against spiders? They kill and eat flies, and other pests.
This basic maths expanded my knowledge. So thank you.
As we know that prime no. is that which has two factorand is divisible by itself and 1 but their factor should not be same. Here 1 has two factor itself and 1 which is same factor so 1 is considered not a prime no.
Divide
connect