Q: If the world is a giant magnet, how come we can’t build a repelling magnet that can float?

Physicist: Three big reasons:

1) The Earth’s magnetic field is hella weak

2) it’s so big and roughly uniform that there’s no reason for a magnet to go one direction or the other

3) floating a magnet in a magnetic field is a delicate balancing act even in the best circumstances.

It turns out that it’s important to keep track of more than just polarity (north/south attract, north/north and south/south repel).  To understand how magnets behave in a magnetic field you also need to consider gradient: the direction in which the field gets stronger and how fast it gets stronger.

“A magnet” or “magnetic dipole”.

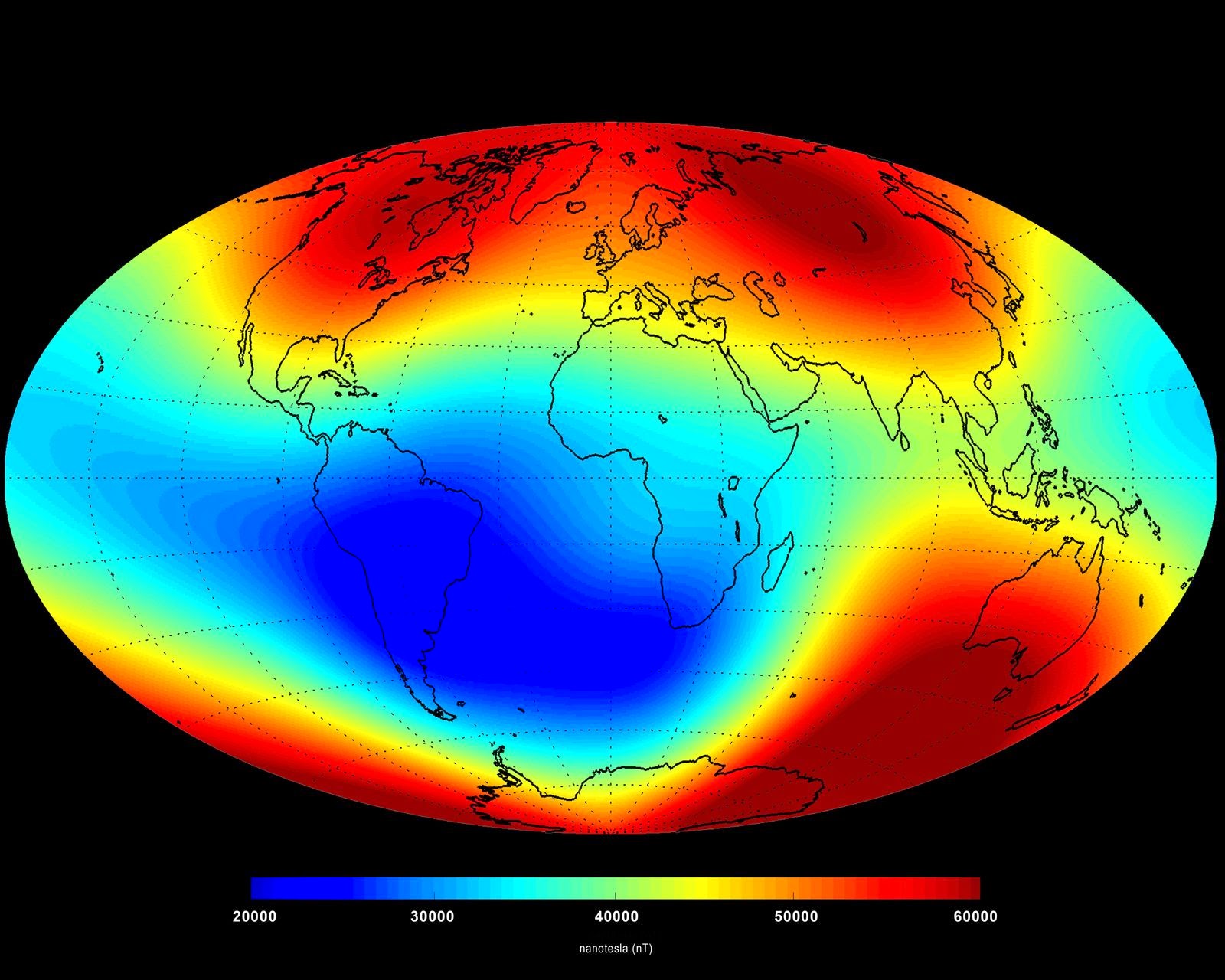
Neodymium magnets (the silver ones that seem like no big deal now, but are really impressive to magnet enthusiasts who grew up with those brittle black magnets back in the day) can support a magnetic field as high as a little over 1 Tesla at their surface.  Earth’s magnetic field is on the order of 1 ten thousandth as strong at its surface.  If you had an electromagnet with the strength of the Earth’s magnetic field, you’d barely be able to pick up paper clips with it.

You might be able to make up for the weakness of Earth’s magnetic field by making your magnet ridiculously strong (somehow), but you’ll quickly run into the second big issue: uniformity.  A uniform magnetic field doesn’t attract or repel magnets, it turns them until they line up.

Placed in a uniform magnetic field a magnet won’t move, but it will rotate to align with that field.

If you have a bar magnet, it’s north and south poles are both basically the same distance from either of the Earth’s poles.  As much as one is pulled, the other is pushed just as strongly.  That’s why compass needles line up with the Earth’s field, but otherwise stay put.  Unfortunately, there’s no way to get a magnet that’s “just north“.  Magnets always come in north/south pairs, so you’ll never get a magnet that simply moves in the direction of the magnetic field.

Fortunately for magnetophiles, physics is complicated.  You may have noticed that a pair of magnets will attract (after aligning with one another).  Despite both of them having a north and a south which will attract and repel one of the poles in the other magnet, a pair of magnets will still manage to attract each other overall.  This is because when the field drops rapidly with distance the pull the closer pole feels is greater than the push that the farther pole feels.  In mathspeak, if the magnetic moment of your magnet is and the external field is , then the force on the magnet is .  The “magnetic gradient” points in the direction in which the strength of the magnetic field increases the fastest (typically, toward the source of the field) and it is bigger for magnetic fields that change quickly over a given distance.  The bigger the gradient, the bigger the total pull (or push) on a magnet.  The Earth’s magnetic gradient is very small because it’s field doesn’t change very fast; if you move a mile in any direction right now, you’ll find the Earth’s magnetic field will be about the same.

So when subjected to a magnetic field a magnet will first rotate to line up and then move toward the strongest part of the field (“in the direction of the gradient”).  If you’re dealing with two magnets, the field is typically strongest at the location of the other magnet, so pairs of magnets tend to snap together.  Were you so inclined, you could figure this out directly by thinking about magnetic dipoles in terms of current loops (a standard way to do things in physics) and then applying Maxwell’s laws.

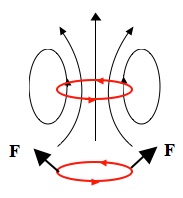
The lower current loop (simple magnet) is attracted to the region with the strongest external magnetic field.  Ultimately, this is why magnets attract each other.

Genuine magnetic levitation is a subtle art.  Earnshaw managed to figure out that there is no way to hold a magnet fixed in space using other magnets.  There a couple of cute exceptions which, by and large, are not helpful in the case of levitating in Earth’s magnetic field.

Left: Diamagnetic water floating in the weakest (but still very strong) part of a magnetic field. Middle: A gyro-stabilized magnet in a peculiarly-shaped field.  Right: A regular magnet held in place by the super-conducting puck below it.

Some materials have properties that only show up in very strong fields.  In particular, diamagnetic stuff (such as water) will flee to the region with the weakest field, which can be in open space.  But this typically requires a field on the order of a hundred thousand times the strength of Earth’s, confined to a very small region.  For only several million dollars we can levitate frogs (and also do important fundamental research or whatever).  This isn’t helpful because it requires both a big magnetic gradient and a powerful field.  Even for the most extreme diamagnetic materials, Earth’s field falls well short.

The “carefully crafted” field needed to levitate a magnetic top.

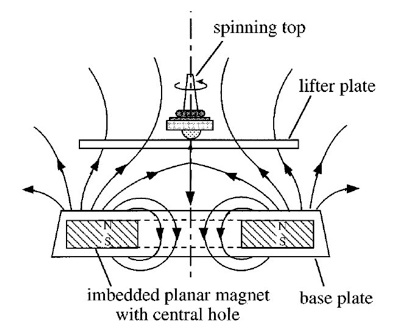
You can also violate Earnshaw’s theorem by removing the “fixed” requirement.  Levitating tops want to flip over and fly toward their magnetic base, but as long as they’re spinning in a properly shaped field, they’re gyro-stabilized.  If the top starts to tip, gyroscopic forces cause its axis (which points in the same direction as its magnet) to tip in such a way that it is pushed upright and back to the middle.  It is not immediately obvious why, but interesting nonetheless.  This sort of levitation requires a very particularly crafted, hourglass-shaped, magnetic field (again, with a large gradient).  Not at all like Earth’s.

Type II superconductors expel magnetic fields but, if forced, they’ll allow the field through in “flux tubes”.  The greater the field, the greater the number of tubes.  It takes a little energy to create or destroy each tube, so superconductors like to keep the field fixed (typically by not moving).  Excitingly, if a nearby region has the same magnetic field, then a superconductor can easily “slide” into it.

Superconductors come in a few different flavors, but the most common are type II (typically written “type II” rather than “type 2”, because physicists like to be fancy).  Type II superconductors are, for lack of a better word, “grumpy” about magnetic fields.  They expel magnetic fields from their interiors, but if you force them to be in a field (using advanced techniques such as “putting them there with your hand”), then the magnetic field lines will instead pierce through the material in tiny tubes.  In this case, rather than expelling them, the material refuses to let the magnetic field change (“Fine…  Good…  That’s exactly how I wanted the field to be.”).  It takes a little energy to create, destroy, or move these “flux tubes” so the superconductor finds itself “pinned” to the magnetic field.  Hence the name: “flux-pinning“.

But a magnetic field is a magnetic field; there’s nothing special about the field in any given place.  If the field is translationally symmetric (if you move in some direction and the field is about the same), then a floating superconductor will be free to slide in that direction.  For example, they’re able to move along tracks (friction free!) because one section of track generates the same field as the next section of track.

Even if we could build a really big “superconductor ship” and pin it to the Earth’s field, we can expect that it wouldn’t float except, perhaps, in a few very particular places.  Generally speaking, the level curves of the Earth’s magnetic field (the surfaces where it has constant strength) intersect the surface.  Ideally, we’d need the magnetic field to increase vertically (the level curves would be horizontal) so that vortex pinning would cause a giant superconductor to maintain altitude.

Best case scenario (assuming you could work with both the tiny field and the tiny gradient), a superconductor ship would experience these level curves as nested invisible walls in space that typically intersect the ground.  Worse, these “walls” aren’t terribly smooth; the Earth’s magnetic field is lumpy and variable.  You could expect your ship to constantly have to force its way through Earth’s field’s ever-varying shape.

The strength of Earth’s lumpy magnetic field.

Without some method for sliding up those “walls”, trying to use superconductors to float in Earth’s magnetic field is mostly just a way of restricting movement across Earth’s surface.  But by the time you’re doing that, you might want to consider any of the many better alternatives to levitation.

Better alternatives.

Given the methods we have for magnetic levitation, the Earth’s magnetic field is severely lacking.

The “loops in a magnetic field” picture is from here.

The “carefully crafted magnetic field” picture is from here (along with a brief discussion of how those things work).