Q: If time is relative, then how can we talk about how old the universe is?

Physicist: One of the most profound insights ever made by peoplekind is that time is relative.  This isn’t some abstract idea, mistake, or mathematical artifact.  If you have two identically functioning clocks, you can start them together, move them to different locations or along different paths, then when you physically bring them back together to compare, they will literally have registered different amounts of time.

You may be inclined to say, “sure, it’s weird… but which clock is right?”.  The existentially terrifying answer is: there is no such thing as a “correct clock”.  Every clock measures its own time and there is no such thing as a universal time.  And yet, cosmologists are always talking about the age of the universe (a mere 13.80±0.02 billion years young).  When talking about the age of the universe we’re talking about the age of everything in it.  But how can we possibly talk about the age of the universe if everything in it has its own personal time?

The short answer is: almost everything is about the same age.  The biggest time discrepancy is between things deep inside of galaxies and things well outside of galaxies, amounting to a couple parts per million (or one or two seconds per week).  Matter that has been in the middle of large galaxies since early in the universe’s history should be no more than on the order of 50,000 years younger than matter that has managed to remain in intergalactic space.  Considering that our best estimates for the age of the universe are only accurate to within 20 million years or so (0.1% relative error), a few dozen millennia here and there doesn’t make any difference.

There are two ways to get clocks to disagree: the twin paradox and gravitational time dilation.  The twin paradox a bizarre consequence of the difference between ordinary geometry and spacetime geometry.  In ordinary geometry, the shortest distance between two points is a straight line.  In spacetime geometry, the longest time between two points is a straight line.  A “straight line” in spacetime includes sitting still, so if you start with two clocks in the same place and take one on a trip that eventually brings it back to its stationary partner, then the traveling clock will have fallen behind its sedentary twin.

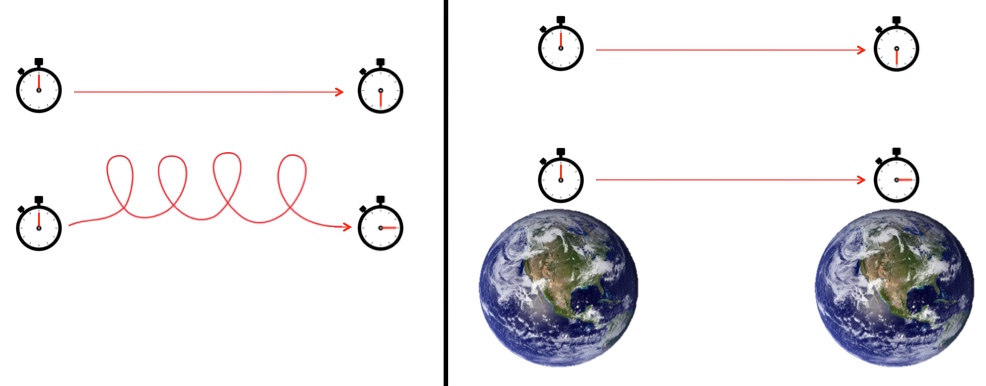
The Twin Paradox: The straighter the path taken between two locations, the more time is experienced.  Gravitational Time Dilation: Things farther from mass experience more time.

Assuming that the traveling clock travels at a more-or-less constant speed, you can figure out how much less time it experiences pretty easily.  If the traveling clock experiences amount of time and the stationary clock experiences amount of time, then (which you’ll notice is always less than t) where v is the speed of the traveling clock and c is the speed of light.  The ratio between these two times is called “gamma”, , which is a useful piece of math to be aware of.  If the traveling clock changes speed, v(t), then you’ll need calculus, , but there are worse things.

Gravitational time dilation is caused by the warping of spacetime caused by the presence of energy and matter (mostly matter) which is a shockingly difficult thing to figure out.  When Einstein initially wrote down the equations that describe the relationship between mass/energy and spacetime he didn’t really expect them to be solved (other than the trivial empty-space solution); it took Schwarzschild to figure out the shape of spacetime around spherical objects (which is useful, considering how much round stuff there is to be found in space).  He did such a good job that the event horizon of a black hole, the boundary beyond which nothing escapes, is known in fancy science circles as the “schwarzschild radius”.

Fortunately, for reasonable situations (not-black-hole situations), you can calculate the time dilation between different altitudes by figuring out how fast a thing would be falling if it made the trip from the top height to the bottom height.  Once you’ve got that speed, v, you plug it into and wham!, you’ve calculated the time dilation due to gravity.  If you want to figure out the total dilation between, say, the surface of the Earth and a point “infinitely far away” (far enough away that Earth can be ignored), then you use the speed something would be falling if it fell from deep space: the escape velocity.

By and large, the effect from the twin paradox is smaller than the effect from gravity, because if something is traveling faster than the local escape velocity, then it escapes.  So the velocity you plug into gamma for the twin paradox (the physical velocity) is lower than the velocity you’d plug in for gravitational dilation (the escape velocity).  If you have some stars swirling about in a galaxy, then you can be pretty sure that they’re moving well below the escape velocity.

The escape velocity from the surface of the Earth is 11km/s, which yields a gamma of .  Being really close to 1 means that the passage of time far from Earth vs. the surface of the Earth are practically the same; an extra 2 seconds per century if you’re hanging out in deep space.  The escape velocity from the core of a large galaxy (such as ours) is on the order of a thousand km/s.  That’s a gamma around , which accounts for that several seconds per week.

Point is, it doesn’t make too much difference where you are in the universe: time is time.

Now admittedly, there are examples of things either trapped in black holes or screaming across the universe at near the speed of light, but the good news for us (on both counts) is that such stuff is rare.  The only things that move anywhere close to the speed of light is light itself (no surprise) and occasionally individual particles of matter.  Light literally experiences zero time, so the “oldest” photons are still newborns; they have a very different notion of how old the universe is.  No one is entirely sure how much of the matter in the universe is presently tied up in black holes, but it’s generally assumed to be a small fraction of the total.

Long story short: when someone says that the universe is 13.8 billion years old, they’re talking about the age of the matter in the universe, almost all of which is effectively the same age.