Physicist: When wondering across the vast plains of the internet, you may have come across this bizarre fact, that 
An unfortunate conclusion may be to say “math is a painful, incomprehensible mystery and I’m not smart enough to get it”. But rest assured, if you think that 
Number theorists get very excited about the “Riemann Zeta Function”, ζ(s), which is equal to 
The bigger s is, the smaller each term, 
You know what this bridge would do if it kept going. “Analytic continuation” is essentially the same idea; take a function that stops (perhaps unnecessarily) and continue it in exactly the way you’d expect.
The analytic continuation of a function is unique, so nailing down ζ(s) for s>1 is all you need to continue it out into the complex plane.
Complex numbers take the form “A+Bi” (where 
That blow up at s=1 seems insurmountable on the real number line, but in the complex plane you can just walk around it to see what’s on the other side.
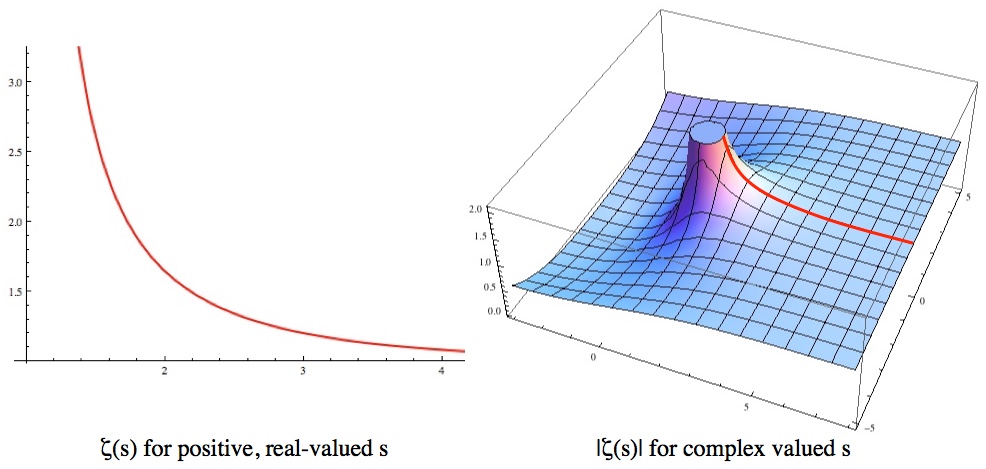
Left: ζ(s) for values of s>1 on the real number line. Right: The same red function surrounded by its “analytic continuation” into the rest of the complex plane. Notice that, except for s=1, ζ(s) is completely smooth and well behaved.
But that’s no problem for a mathematician (see the answer gravy below). You can follow ζ(s) from the large real numbers (where the summation definition makes sense), around the blow up at s=1, to s=-1 where you find a completely mundane value. It’s
So the 
This shows up outside of number theory. In order to model particle interactions correctly, it’s important to take into account every possible way for that interaction to unfold. This means taking an infinite sum, which often goes well (produces a finite result), but sometimes doesn’t. It turns out that physical laws really like functions that make sense in the complex plane. So when “1+2+3+…” started showing up in calculations of certain particle interactions, physicists turned to the Riemann Zeta function and found that using -1/12 actually turned out to be the right thing to do (in physics “the right thing to do” means “the thing that generates results that precisely agree with experiment”).
A less technical shortcut (or at least a shortcut with the technicalities swept under the rug) for why the summation is -1/12 instead of something else can be found here. For exactly why ζ(-1)=-1/12, see below.
Answer Gravy: Figuring out that ζ(-1)=-1/12 takes a bit of work. You have to find an analytic continuation that covers s=-1, and then actually evaluate it. Somewhat surprisingly, this is something you can do by hand.
Often, analytically continuing a function comes down to re-writing it in such a way that its “poles” (the locations where it blows up) don’t screw things up more than they absolutely have to. For example, the function 
f(z) can be explicitly written without a summation, unlike ζ(s), which gives us some insight into why it stops making sense for |z|≥1. It just so happens that for |z|<1, 
Finding an analytic continuation for ζ(s) is a lot trickier, because there’s no cute way to write it without using an infinite summation (or product), but the basic idea is the same. We’re going to do this in two steps: first turning ζ(s) into an alternating sum that converges for s>0 (except s=1), then turning that into a form that converges everywhere (except s=1).
For seemingly no reason, multiply ζ(s) by (1-21-s):
![\begin{array}{ll} &\left(1-2^{1-s}\right)\zeta(s)\\[2mm] =&\left(1-2^{1-s}\right)\sum_{n=1}^\infty\frac{1}{n^s}\\[2mm] =&\sum_{n=1}^\infty\frac{1}{n^s}-2^{1-s}\sum_{n=1}^\infty\frac{1}{n^s}\\[2mm] =&\sum_{n=1}^\infty\frac{1}{n^s}-2\sum_{n=1}^\infty\frac{1}{(2n)^s}\\[2mm] =&\left(\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\ldots\right)-2\left(\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{6^s}+\frac{1}{8^s}+\ldots\right)\\[2mm] =&\frac{1}{1^s}-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+\ldots\\[2mm] =&\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}\\[2mm] =&\sum_{n=0}^\infty\frac{(-1)^{n}}{(n+1)^s} \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bll%7D++++%26%5Cleft%281-2%5E%7B1-s%7D%5Cright%29%5Czeta%28s%29%5C%5C%5B2mm%5D++%3D%26%5Cleft%281-2%5E%7B1-s%7D%5Cright%29%5Csum_%7Bn%3D1%7D%5E%5Cinfty%5Cfrac%7B1%7D%7Bn%5Es%7D%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bn%3D1%7D%5E%5Cinfty%5Cfrac%7B1%7D%7Bn%5Es%7D-2%5E%7B1-s%7D%5Csum_%7Bn%3D1%7D%5E%5Cinfty%5Cfrac%7B1%7D%7Bn%5Es%7D%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bn%3D1%7D%5E%5Cinfty%5Cfrac%7B1%7D%7Bn%5Es%7D-2%5Csum_%7Bn%3D1%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B%282n%29%5Es%7D%5C%5C%5B2mm%5D++%3D%26%5Cleft%28%5Cfrac%7B1%7D%7B1%5Es%7D%2B%5Cfrac%7B1%7D%7B2%5Es%7D%2B%5Cfrac%7B1%7D%7B3%5Es%7D%2B%5Cfrac%7B1%7D%7B4%5Es%7D%2B%5Cldots%5Cright%29-2%5Cleft%28%5Cfrac%7B1%7D%7B2%5Es%7D%2B%5Cfrac%7B1%7D%7B4%5Es%7D%2B%5Cfrac%7B1%7D%7B6%5Es%7D%2B%5Cfrac%7B1%7D%7B8%5Es%7D%2B%5Cldots%5Cright%29%5C%5C%5B2mm%5D++%3D%26%5Cfrac%7B1%7D%7B1%5Es%7D-%5Cfrac%7B1%7D%7B2%5Es%7D%2B%5Cfrac%7B1%7D%7B3%5Es%7D-%5Cfrac%7B1%7D%7B4%5Es%7D%2B%5Cldots%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bn%3D1%7D%5E%5Cinfty%5Cfrac%7B%28-1%29%5E%7Bn-1%7D%7D%7Bn%5Es%7D%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bn%3D0%7D%5E%5Cinfty%5Cfrac%7B%28-1%29%5E%7Bn%7D%7D%7B%28n%2B1%29%5Es%7D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{ll} &\left(1-2^{1-s}\right)\zeta(s)\\[2mm] =&\left(1-2^{1-s}\right)\sum_{n=1}^\infty\frac{1}{n^s}\\[2mm] =&\sum_{n=1}^\infty\frac{1}{n^s}-2^{1-s}\sum_{n=1}^\infty\frac{1}{n^s}\\[2mm] =&\sum_{n=1}^\infty\frac{1}{n^s}-2\sum_{n=1}^\infty\frac{1}{(2n)^s}\\[2mm] =&\left(\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\ldots\right)-2\left(\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{6^s}+\frac{1}{8^s}+\ldots\right)\\[2mm] =&\frac{1}{1^s}-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+\ldots\\[2mm] =&\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}\\[2mm] =&\sum_{n=0}^\infty\frac{(-1)^{n}}{(n+1)^s} \end{array}")
So we’ve got a new version of the Zeta function, 
There’s a clever old trick for shoehorning a summation into converging: Euler summation. Euler (who realizes everything) realized that 
![\begin{array}{rcl} \sum_{k=0}^\infty A_k&=&\sum_{k=0}^\infty \left(\sum_{n=k}^\infty {n\choose k}\frac{y^{k+1}}{(1+y)^{n+1}}\right)A_k\\[2mm] &=&\sum_{k=0}^\infty \sum_{n=k}^\infty {n\choose k}\frac{y^{k+1}}{(1+y)^{n+1}}A_k\\[2mm] &=&\sum_{n=0}^\infty \sum_{k=0}^n {n\choose k}\frac{y^{k+1}}{(1+y)^{n+1}}A_k\\[2mm] &=&\sum_{n=0}^\infty \frac{1}{(1+y)^{n+1}}\sum_{k=0}^n {n\choose k}y^{k+1}A_k\\[2mm] \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++%5Csum_%7Bk%3D0%7D%5E%5Cinfty+A_k%26%3D%26%5Csum_%7Bk%3D0%7D%5E%5Cinfty+%5Cleft%28%5Csum_%7Bn%3Dk%7D%5E%5Cinfty+%7Bn%5Cchoose+k%7D%5Cfrac%7By%5E%7Bk%2B1%7D%7D%7B%281%2By%29%5E%7Bn%2B1%7D%7D%5Cright%29A_k%5C%5C%5B2mm%5D++%26%3D%26%5Csum_%7Bk%3D0%7D%5E%5Cinfty+%5Csum_%7Bn%3Dk%7D%5E%5Cinfty+%7Bn%5Cchoose+k%7D%5Cfrac%7By%5E%7Bk%2B1%7D%7D%7B%281%2By%29%5E%7Bn%2B1%7D%7DA_k%5C%5C%5B2mm%5D++%26%3D%26%5Csum_%7Bn%3D0%7D%5E%5Cinfty+%5Csum_%7Bk%3D0%7D%5En+%7Bn%5Cchoose+k%7D%5Cfrac%7By%5E%7Bk%2B1%7D%7D%7B%281%2By%29%5E%7Bn%2B1%7D%7DA_k%5C%5C%5B2mm%5D++%26%3D%26%5Csum_%7Bn%3D0%7D%5E%5Cinfty+%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bn%2B1%7D%7D%5Csum_%7Bk%3D0%7D%5En+%7Bn%5Cchoose+k%7Dy%5E%7Bk%2B1%7DA_k%5C%5C%5B2mm%5D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{rcl} \sum_{k=0}^\infty A_k&=&\sum_{k=0}^\infty \left(\sum_{n=k}^\infty {n\choose k}\frac{y^{k+1}}{(1+y)^{n+1}}\right)A_k\\[2mm] &=&\sum_{k=0}^\infty \sum_{n=k}^\infty {n\choose k}\frac{y^{k+1}}{(1+y)^{n+1}}A_k\\[2mm] &=&\sum_{n=0}^\infty \sum_{k=0}^n {n\choose k}\frac{y^{k+1}}{(1+y)^{n+1}}A_k\\[2mm] &=&\sum_{n=0}^\infty \frac{1}{(1+y)^{n+1}}\sum_{k=0}^n {n\choose k}y^{k+1}A_k\\[2mm] \end{array}")
If the original sum converges, then this will converge to the same thing, but it may also converge even when the original sum doesn’t. That’s exactly what you’re looking for when you want to create an analytic continuation; it agrees with the original function, but continues to work over a wider domain.
This looks like a total mess, but it’s stunningly useful. If we use Euler summation with y=1, we create a summation that analytically continues the Zeta function to the entire complex plane: a “globally convergent form”. Rather than a definition that only works sometimes (but is easy to understand), we get a definition that works everywhere (but looks like a horror show).
![\begin{array}{rcl} \zeta(s)&=&\frac{1}{1-2^{1-s}}\sum_{k=0}^\infty\frac{(-1)^{k}}{(k+1)^s}\\[2mm] &=&\frac{1}{1-2^{1-s}}\sum_{n=0}^\infty\frac{1}{(1+y)^{n+1}}\sum_{k=0}^n{n\choose k}y^{k+1}\frac{(-1)^{k}}{(k+1)^s}\\[2mm] &=&\frac{1}{1-2^{1-s}}\sum_{n=0}^\infty\frac{1}{(1+1)^{n+1}}\sum_{k=0}^n{n\choose k}1^{k+1}\frac{(-1)^{k}}{(k+1)^s}\\[2mm] &=&\frac{1}{1-2^{1-s}}\sum_{n=0}^\infty\frac{1}{2^{n+1}}\sum_{k=0}^n{n\choose k}\frac{(-1)^{k}}{(k+1)^s}\\[2mm] \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++%5Czeta%28s%29%26%3D%26%5Cfrac%7B1%7D%7B1-2%5E%7B1-s%7D%7D%5Csum_%7Bk%3D0%7D%5E%5Cinfty%5Cfrac%7B%28-1%29%5E%7Bk%7D%7D%7B%28k%2B1%29%5Es%7D%5C%5C%5B2mm%5D++%26%3D%26%5Cfrac%7B1%7D%7B1-2%5E%7B1-s%7D%7D%5Csum_%7Bn%3D0%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bn%2B1%7D%7D%5Csum_%7Bk%3D0%7D%5En%7Bn%5Cchoose+k%7Dy%5E%7Bk%2B1%7D%5Cfrac%7B%28-1%29%5E%7Bk%7D%7D%7B%28k%2B1%29%5Es%7D%5C%5C%5B2mm%5D++%26%3D%26%5Cfrac%7B1%7D%7B1-2%5E%7B1-s%7D%7D%5Csum_%7Bn%3D0%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B%281%2B1%29%5E%7Bn%2B1%7D%7D%5Csum_%7Bk%3D0%7D%5En%7Bn%5Cchoose+k%7D1%5E%7Bk%2B1%7D%5Cfrac%7B%28-1%29%5E%7Bk%7D%7D%7B%28k%2B1%29%5Es%7D%5C%5C%5B2mm%5D++%26%3D%26%5Cfrac%7B1%7D%7B1-2%5E%7B1-s%7D%7D%5Csum_%7Bn%3D0%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B2%5E%7Bn%2B1%7D%7D%5Csum_%7Bk%3D0%7D%5En%7Bn%5Cchoose+k%7D%5Cfrac%7B%28-1%29%5E%7Bk%7D%7D%7B%28k%2B1%29%5Es%7D%5C%5C%5B2mm%5D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{rcl} \zeta(s)&=&\frac{1}{1-2^{1-s}}\sum_{k=0}^\infty\frac{(-1)^{k}}{(k+1)^s}\\[2mm] &=&\frac{1}{1-2^{1-s}}\sum_{n=0}^\infty\frac{1}{(1+y)^{n+1}}\sum_{k=0}^n{n\choose k}y^{k+1}\frac{(-1)^{k}}{(k+1)^s}\\[2mm] &=&\frac{1}{1-2^{1-s}}\sum_{n=0}^\infty\frac{1}{(1+1)^{n+1}}\sum_{k=0}^n{n\choose k}1^{k+1}\frac{(-1)^{k}}{(k+1)^s}\\[2mm] &=&\frac{1}{1-2^{1-s}}\sum_{n=0}^\infty\frac{1}{2^{n+1}}\sum_{k=0}^n{n\choose k}\frac{(-1)^{k}}{(k+1)^s}\\[2mm] \end{array}")
This is one of those great examples of the field of mathematics being too big for every discovery to be noticed. This formulation of ζ(s) was discovered in the 1930s, forgotten for 60 years, and then found in an old book.
For most values of s, this globally convergent form isn’t particularly useful for us “calculate it by hand” folk, because it still has an infinite sum (and adding an infinite number of terms takes a while). Very fortunately, there’s another cute trick we can use here. When n>d, 
So finally, we plug s=-1 into ζ(s)
![\begin{array}{rcl} \zeta(-1)&=&\frac{1}{1-2^{2}}\sum_{n=0}^\infty\frac{1}{2^{n+1}}\sum_{k=0}^n{n\choose k}(-1)^{k}(k+1)\\[2mm] &=&-\frac{1}{3}\sum_{n=0}^1\frac{1}{2^{n+1}}\sum_{k=0}^n{n\choose k}(-1)^{k}(k+1)\\[2mm] &=&-\frac{1}{3}\cdot\frac{1}{2^{0+1}}{0\choose 0}(-1)^{0}(0+1)-\frac{1}{3}\cdot\frac{1}{2^{1+1}}{1\choose 0}(-1)^{0}(0+1)-\frac{1}{3}\cdot\frac{1}{2^{1+1}}{1\choose 1}(-1)^{1}(1+1)\\[2mm] &=&-\frac{1}{3}\cdot\frac{1}{2}\cdot1\cdot1\cdot1-\frac{1}{3}\cdot\frac{1}{4}\cdot1\cdot1\cdot1-\frac{1}{3}\cdot\frac{1}{4}\cdot1\cdot(-1)\cdot2\\[2mm] &=&-\frac{1}{6}-\frac{1}{12}+\frac{1}{6}\\[2mm] &=&-\frac{1}{12} \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++%5Czeta%28-1%29%26%3D%26%5Cfrac%7B1%7D%7B1-2%5E%7B2%7D%7D%5Csum_%7Bn%3D0%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B2%5E%7Bn%2B1%7D%7D%5Csum_%7Bk%3D0%7D%5En%7Bn%5Cchoose+k%7D%28-1%29%5E%7Bk%7D%28k%2B1%29%5C%5C%5B2mm%5D++%26%3D%26-%5Cfrac%7B1%7D%7B3%7D%5Csum_%7Bn%3D0%7D%5E1%5Cfrac%7B1%7D%7B2%5E%7Bn%2B1%7D%7D%5Csum_%7Bk%3D0%7D%5En%7Bn%5Cchoose+k%7D%28-1%29%5E%7Bk%7D%28k%2B1%29%5C%5C%5B2mm%5D++%26%3D%26-%5Cfrac%7B1%7D%7B3%7D%5Ccdot%5Cfrac%7B1%7D%7B2%5E%7B0%2B1%7D%7D%7B0%5Cchoose+0%7D%28-1%29%5E%7B0%7D%280%2B1%29-%5Cfrac%7B1%7D%7B3%7D%5Ccdot%5Cfrac%7B1%7D%7B2%5E%7B1%2B1%7D%7D%7B1%5Cchoose+0%7D%28-1%29%5E%7B0%7D%280%2B1%29-%5Cfrac%7B1%7D%7B3%7D%5Ccdot%5Cfrac%7B1%7D%7B2%5E%7B1%2B1%7D%7D%7B1%5Cchoose+1%7D%28-1%29%5E%7B1%7D%281%2B1%29%5C%5C%5B2mm%5D++%26%3D%26-%5Cfrac%7B1%7D%7B3%7D%5Ccdot%5Cfrac%7B1%7D%7B2%7D%5Ccdot1%5Ccdot1%5Ccdot1-%5Cfrac%7B1%7D%7B3%7D%5Ccdot%5Cfrac%7B1%7D%7B4%7D%5Ccdot1%5Ccdot1%5Ccdot1-%5Cfrac%7B1%7D%7B3%7D%5Ccdot%5Cfrac%7B1%7D%7B4%7D%5Ccdot1%5Ccdot%28-1%29%5Ccdot2%5C%5C%5B2mm%5D++%26%3D%26-%5Cfrac%7B1%7D%7B6%7D-%5Cfrac%7B1%7D%7B12%7D%2B%5Cfrac%7B1%7D%7B6%7D%5C%5C%5B2mm%5D++%26%3D%26-%5Cfrac%7B1%7D%7B12%7D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{rcl} \zeta(-1)&=&\frac{1}{1-2^{2}}\sum_{n=0}^\infty\frac{1}{2^{n+1}}\sum_{k=0}^n{n\choose k}(-1)^{k}(k+1)\\[2mm] &=&-\frac{1}{3}\sum_{n=0}^1\frac{1}{2^{n+1}}\sum_{k=0}^n{n\choose k}(-1)^{k}(k+1)\\[2mm] &=&-\frac{1}{3}\cdot\frac{1}{2^{0+1}}{0\choose 0}(-1)^{0}(0+1)-\frac{1}{3}\cdot\frac{1}{2^{1+1}}{1\choose 0}(-1)^{0}(0+1)-\frac{1}{3}\cdot\frac{1}{2^{1+1}}{1\choose 1}(-1)^{1}(1+1)\\[2mm] &=&-\frac{1}{3}\cdot\frac{1}{2}\cdot1\cdot1\cdot1-\frac{1}{3}\cdot\frac{1}{4}\cdot1\cdot1\cdot1-\frac{1}{3}\cdot\frac{1}{4}\cdot1\cdot(-1)\cdot2\\[2mm] &=&-\frac{1}{6}-\frac{1}{12}+\frac{1}{6}\\[2mm] &=&-\frac{1}{12} \end{array}")
Keen-eyed readers will note that this looks nothing like 1+2+3+… and indeed, it’s not.
(Update: 11/24/17)
A commenter pointed out that it’s a pain to find a proof for why Euler’s sum works. Basically, this comes down to showing that 
You can prove this by counting how often each term, 
![\begin{array}{rl} &\sum_{k=n}^\infty{k\choose n}\frac{1}{(1+y)^{k+1}}\\[2mm] =&{n\choose n}\sum_{k=n}^\infty\frac{1}{(1+y)^{k+1}}+\sum_{k=n}^\infty\left({k+1\choose n}-{k\choose n}\right)\sum_{j=k+1}^\infty \frac{1}{(1+y)^{j+1}}\\[2mm] =&\sum_{k=n}^\infty\frac{1}{(1+y)^{k+1}}+\sum_{k=n}^\infty{k\choose n-1}\sum_{j=k+1}^\infty \frac{1}{(1+y)^{j+1}}\\[2mm] =&\frac{\frac{1}{(1+y)^{n+1}}}{1-\frac{1}{(1+y)}}+\sum_{k=n}^\infty{k\choose n-1}\frac{\frac{1}{(1+y)^{k+2}}}{1-\frac{1}{(1+y)}}\\[2mm] =&\frac{1}{y(1+y)^n}+\sum_{k=n}^\infty{k\choose n-1}\frac{1}{y(1+y)^{k+1}}\\[2mm] =&\sum_{k=n-1}^\infty{k\choose n-1}\frac{1}{y(1+y)^{k+1}}\\[2mm] =&\cdots\\[2mm] =&\sum_{k=0}^\infty{k\choose 0}\frac{1}{y^n(1+y)^{k+1}}\\[2mm] =&\frac{1}{y^n}\sum_{k=0}^\infty\frac{1}{(1+y)^{k+1}}\\[2mm] =&\frac{1}{y^n}\frac{\frac{1}{(1+y)}}{1-\frac{1}{(1+y)}}\\[2mm] =&\frac{1}{y^{n+1}} \end{array}](http://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brl%7D++%26%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%7Bk%5Cchoose+n%7D%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bk%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%7Bn%5Cchoose+n%7D%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bk%2B1%7D%7D%2B%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%5Cleft%28%7Bk%2B1%5Cchoose+n%7D-%7Bk%5Cchoose+n%7D%5Cright%29%5Csum_%7Bj%3Dk%2B1%7D%5E%5Cinfty+%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bj%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bk%2B1%7D%7D%2B%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%7Bk%5Cchoose+n-1%7D%5Csum_%7Bj%3Dk%2B1%7D%5E%5Cinfty+%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bj%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Cfrac%7B%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bn%2B1%7D%7D%7D%7B1-%5Cfrac%7B1%7D%7B%281%2By%29%7D%7D%2B%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%7Bk%5Cchoose+n-1%7D%5Cfrac%7B%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bk%2B2%7D%7D%7D%7B1-%5Cfrac%7B1%7D%7B%281%2By%29%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Cfrac%7B1%7D%7By%281%2By%29%5En%7D%2B%5Csum_%7Bk%3Dn%7D%5E%5Cinfty%7Bk%5Cchoose+n-1%7D%5Cfrac%7B1%7D%7By%281%2By%29%5E%7Bk%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bk%3Dn-1%7D%5E%5Cinfty%7Bk%5Cchoose+n-1%7D%5Cfrac%7B1%7D%7By%281%2By%29%5E%7Bk%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Ccdots%5C%5C%5B2mm%5D++%3D%26%5Csum_%7Bk%3D0%7D%5E%5Cinfty%7Bk%5Cchoose+0%7D%5Cfrac%7B1%7D%7By%5En%281%2By%29%5E%7Bk%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Cfrac%7B1%7D%7By%5En%7D%5Csum_%7Bk%3D0%7D%5E%5Cinfty%5Cfrac%7B1%7D%7B%281%2By%29%5E%7Bk%2B1%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Cfrac%7B1%7D%7By%5En%7D%5Cfrac%7B%5Cfrac%7B1%7D%7B%281%2By%29%7D%7D%7B1-%5Cfrac%7B1%7D%7B%281%2By%29%7D%7D%5C%5C%5B2mm%5D++%3D%26%5Cfrac%7B1%7D%7By%5E%7Bn%2B1%7D%7D++%5Cend%7Barray%7D&bg=ffffff&fg=000&s=0 "\begin{array}{rl} &\sum_{k=n}^\infty{k\choose n}\frac{1}{(1+y)^{k+1}}\\[2mm] =&{n\choose n}\sum_{k=n}^\infty\frac{1}{(1+y)^{k+1}}+\sum_{k=n}^\infty\left({k+1\choose n}-{k\choose n}\right)\sum_{j=k+1}^\infty \frac{1}{(1+y)^{j+1}}\\[2mm] =&\sum_{k=n}^\infty\frac{1}{(1+y)^{k+1}}+\sum_{k=n}^\infty{k\choose n-1}\sum_{j=k+1}^\infty \frac{1}{(1+y)^{j+1}}\\[2mm] =&\frac{\frac{1}{(1+y)^{n+1}}}{1-\frac{1}{(1+y)}}+\sum_{k=n}^\infty{k\choose n-1}\frac{\frac{1}{(1+y)^{k+2}}}{1-\frac{1}{(1+y)}}\\[2mm] =&\frac{1}{y(1+y)^n}+\sum_{k=n}^\infty{k\choose n-1}\frac{1}{y(1+y)^{k+1}}\\[2mm] =&\sum_{k=n-1}^\infty{k\choose n-1}\frac{1}{y(1+y)^{k+1}}\\[2mm] =&\cdots\\[2mm] =&\sum_{k=0}^\infty{k\choose 0}\frac{1}{y^n(1+y)^{k+1}}\\[2mm] =&\frac{1}{y^n}\sum_{k=0}^\infty\frac{1}{(1+y)^{k+1}}\\[2mm] =&\frac{1}{y^n}\frac{\frac{1}{(1+y)}}{1-\frac{1}{(1+y)}}\\[2mm] =&\frac{1}{y^{n+1}} \end{array}")
That “…” step means “repeat n times”. It’s worth mentioning that this only works for |1+y|>1 (otherwise the infinite sums diverge). Euler summations change how a summation is written, and can accelerate convergence (which is really useful), but if the original sum converges, then the new sum will converge to the same thing.
Maple plots, right? I love Maple…
I widely disagree with you, the sum is not at all about “math enthusiasts being so (justifiably) excited about ζ(s) that they misapply it, and has nothing to do with what 1+2+3+… actually equals.” The issue here is how we define summation, not what the “actual value” is, such a thing does not exist (it always relies on axioms and, well, we can use other axioms for addition).
Ramanujan once derived the same formula without using ζ (yet I must say the demonstration was not rigorous), and Euler once basically said there’s no big deal with this kind of sums being equal to nonsensical values, as long as we take a wider definition of what a sum is (“Mais j’ai déjà remarqué dans une autre occaſion, qu’il faut donner au mot ſomme une ſignification plus étendue, & entendre par là une fraction, ou toute autre expreſſion analytique”, http://eulerarchive.maa.org//docs/originals/E352.pdf, second page, pardon my french). Terence Tao also wrote about this (disclosure alert, I got quickly lost in the maths): https://terrytao.wordpress.com/2010/04/10/the-euler-maclaurin-formula-bernoulli-numbers-the-zeta-function-and-real-variable-analytic-continuation/
My point is, with the usual definition of what a sum is, then yes, 1 + 2 + 3 +… = ∞. However, when we take a wider definition of the sum, with some new assumptions and new considerations, then 1 + 2 + 3 + … = -1/12.
And that’s not illogical! We’ve done it many times before. For instance, the usual definition of the sum does not allow infinite sums. That’s preposterous, we would say, to imagine one can add an infinite number of elements. The sum cannot exist as we continuously add new terms, and the partial sum is always changing! (see Zeno’s paradoxes). Then we introduced the concept of limits, and said: “welp, now infinite sums are sometimes equal to a real number, and 1 + 1/2 + 1/4 + … = 2. Now you can tell jokes about a bar and an infinite number of mathematicians coming in, no need to thank me”. And that was only 200 years ago.
I mean, we’ve redefined addition many times by now. At first, addition was exclusively between positive numbers, and subtraction could only yield positive numbers (how can you remove 8 apples from 5 and a half apples? Well you can’t, that does not make any sense). Then, and not necessarily in that order, we redefined addition so we could add negative numbers, and even complex numbers. Even though each time, it did not make any sense. Then we also redefined addition so that we could add an infinite amount of numbers and shut Zeno’s mouth once and for all, even though that did not make any sense. But we would not redefine the addition for divergent series because it does not make any sense? Come on.
In a nutshell (I got a bit carried away, sorry), it all depends on your definition of what summation is. So as I said before:
* 1 + 2 + 3 + … = -1/12 if you like divergent series theory or analytic prolongations;
* 1 + 2 + 3 + … = ∞ if you don’t but still like infinite summations;
* 1 + 2 + 3 + … = Error if you don’t like infinite summations (or infinity).
And that’s okay. We don’t always need divergent series, but there’s no need to ban them just because they look so weird.
What I usually say on math forums when I see highschool students posting about this is “it’s technically true, but not with the sum you are used to.” This way I feel I’m not lying to them and they won’t try and drive their teachers crazy.
That’s just my opinion, feel free to disagree or argue with me!
Another example that proves mathematicians work in the realm of fantasy and not reality.
Why are you dividing by zero?
zeta(s) = sum( {n = 0 … infinity} (1/n)^s )
@Shawn H Corey
Good catch!
I should not have and it is fixed.
@Traruh Synred
Mathematica.
Cesaro summation provides another, more intuitive path to reach the same -1/12 result that doesn’t involve the analytic continuation of the zeta function. It’s essentially just taking the limit as N->infinity of the average of all partial sums up to N (rather than just taking the limit of partial sums, as we normally define infinite summation.)
When a physicist uses “sum(n) for n from 1 to infinity = -1/12”, as they very rarely do, they are usually doing so in the context of a perturbation theory where they’ve written down a series of terms which are diverging linearly, and they can argue that Cesaro summation is the physically meaningful interpretation of their infinite sum.
https://en.wikipedia.org/wiki/Ces%C3%A0ro_summation
https://en.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_%E2%8B%AF#Summability
I hate to be the one disputing this, but this post has several inaccuracies.
ς(s) = Σ[n = 1, Infinity](n^(-s)) is true by definition, not by coincidence. Thus, you’re wrong that the Riemann-Zeta function is a function which happens to agree with the given sum whenever Re(s) > 1. No, this is false: the function is DEFINED as the sum, so the function is inherently undefined wherever the sum is undefined.
It is also wrong to say that the function is the summation if Re(s) > 1, and the analytical continuation otherwise. The Taylor series of the natural exponential function, which is its analytical continuation, is not different from the function itself and not different from the expression which defines the function. Similarly, the analytical continuation of the factorial function, which is the Gamma function, it is not different from the shifter factorial function. Rather, they are equal everywhere in the complex plane. The analytical continuation of a function is equal to this function everywhere, because all this continuation does is extend the domain on which the function is defined. However, the issue is that the analytic continuation of a function can be represented by multiple expressions, and these can sometimes be not valid in certain regions of the domain. The advantage is that whenever one expression does not apply, one can use a different expression to compensate, and the reason it works is because the analytical continuation is unique AND the analytical continuation is not defined as one of these expressions we use to represent it. A satisfactory representation of the analytical continuation of a function will agree with the function in every region of the domain where the function had been previously defined, but then it’ll provide outputs for inputs where the function was not previously defined, thus extending the domain. This is how it works with every other example I mentioned previously, there is no reason the Riemann-Zeta function would be any different. This is also how the notion of half-iterations was extended to the complex numbers in fractional calculus. Hence, because the analytical continuation agrees with the function everywhere, and since the function is DEFINED as the sum everywhere, then this means that the analytical continuation extends the domain on which these sums are defined, which is perfectly logical, consistent, and acceptable in mathematics.
This being said, there are other comments I have:
1. You cannot say the sum is infinity, because infinity is not a number. You cannot talk about numerical expressions being equal to infinity. You can only say that the limit as the input approaches infinity of a certain parameter of a relation or sequence is infinity, but this is different from the expression itself. The sequence of the triangular numbers approaches infinity, but this says nothing about whether the “completed” summation is infinite or not. You can only say that the limit of the sequence of partial sums of a series is equal to the series itself in cases of convergence. If there is no convergence, then it is incorrect to say that this limit equals the series, so it is incorrect to say that any diverging series is strictly equal to infinity. Otherwise, you get contradictions.
2. Historically, the result that 1 + 2 + 3 + … = -1/12 is older than number theory and than the analytical continuation. Euler and other mathematicians of the 19th and even 18th century had already made their conjectures that this equation was true, and they had their justifications for it.
3. There are several other methods to prove this equation true aside from the Riemann-Zeta function. There is Ramanujan Summation, Abel Summation, stronger iterations of Cèsaro’s theorems and iterations, and there’s are even modern methods which areextra rigorous which allow us to say the equation is true, and these methods serve actually a generalization to the definition of convergence. For more info, check this: https://terrytao.wordpress.com/2010/04/10/the-euler-maclaurin-formula-bernoulli-numbers-the-zeta-function-and-real-variable-analytic-continuation/#comment-489088
Okay, what about how the series 1 – 2 + 3 – 4 + … is usually stated to “sum” to 1/4?
You don’t even need super abstract number theory stuff to arrive at that conclusion; you can simply add 4 copies of it together using nothing but shifting and term-by-term addition, and arrive at 1 (meaning each version of it is 1/4), as demonstrated at https://en.wikipedia.org/wiki/1_%E2%88%92_2_%2B_3_%E2%88%92_4_%2B_%E2%8B%AF#Stability_and_linearity. And although it can be argued that doing so isn’t mathematically rigorous, more rigorous methods of summing infinite series do agree with this answer, so it feels like there’s something to it.
Hi,
great article. How that Euler summation works? – I din’t find a proof of it…
Thank you
@Ángel Méndez Rivera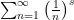
as you approach Re[s]=1. Maybe I should do that.
I sincerely appreciate your comments.
It is true that the Taylor expansion of e^x is the same as e^x, but only because that Taylor polynomial converges globally. I included that “1/(1-x)=1+x+x^2+…” example to underscore exactly that. If you plug “2” into the fraction you get “-1”, but if you plug it into the sum you get “undefined”. Within the radius of convergence, the expressions are interchangeable, but outside they’re not.
1) Of course you’re right. I should say “the partial sum increases monotonically without bound”, but if you ask ten people on the street what that means (after explaining it), nine of them will say “you mean infinity?”. I figured that the people who already know about this subtlety will understand what I’m saying, and the folk who don’t, don’t need another thing to bog them down. It’s already a really dense post. The alternative was a more in-depth discussion of the divergence of
2-3) The -1/12 thing is definitely very old, and you don’t need continuation to get to it. That’s why I tried to describe continuation in terms of continuing the function “exactly as you’d expect”. Continuation produces results that are both reasonable and unique, and correspond with the sort of conclusion you might stumble upon in any number of ways. For example, the continuation of any polynomial on the reals is just the same polynomial on the complex numbers. Totally reasonable. Generally speaking, if you can find a nice, simple extension that continues to make sense, it will (often) be the analytic continuation.
Hey,
Just though I would point this out i = sqrt(-1) can be a bit misleading(and at times give a wrong understanding), wouldn’t it be better to define it as i^2 = -1? To avoid the inherent issues.
Cheers
@Hari Seldon
You’re right! I guess if I could see the future of entire civilizations, I would have seen that too Mr. Seldon.
Fixed.
Yes there are many ways to get this result, but they all make the same blunder. This -1/12 result is simply one huge mistake!
The mistake is one of taking a function that applies to just positive whole numbers, manipulating it in ways that bring fractions and negative numbers into play (such as by using division and subtraction operations), and then interpreting the result as though it still relates to positive whole numbers.
Consider the endless sum 1 + 2 + 3 + 4 + … In order to add up the first four terms we substitute n=4 into the formula n(n+1)/2. If we pretend this does not just apply to positive integers, we might plot this as the graph for y = x(x+1)/2 as I’ve done here: https://tinyurl.com/y9ukc84k
To the right of the origin, the area under the curve represents the increasing partial sum. We can see that it is equal and opposite to the area to the left of the line x= -1 and if we cancel these two areas, then the ‘sum’ that remains is the area under the curve between 0 and minus 1. This corresponds to the mysterious minus one twelfth value (& can be calculated as the definite integral between -1 and 0).
Just as -1/12 is supposedly the sum of all natural numbers, it is claimed that the ‘sum of the squares of natural numbers’ (and indeed any even power) is supposedly zero, and the ‘sum of the cubes of the natural numbers’ is supposedly equal to or related to 1/120. Again these values are the simply the limit of the area of the respective partial sum expressions between -1 and 0.
If we want a function for the nth sum of positive or negative numbers then we can use n(|n|+1)/2. Here we are simply taking the absolute value of the second n. If we pretend this does not just apply to integers, we might plot this as the graph for y = x(sqrt(x*x)+1)/2 as I’ve done here: https://tinyurl.com/y8ekwj82
This graph is exactly the same as the other graph for the positive values, but now it is symmetrical about the axis and so there is no longer any way to manipulate the areas under the curves (the ‘sums’) to get a resulting ‘sum’ of -1/12.
Similarly, if the Zeta function had been expressed using absolute values where required, then the analytic continuation might have produced a graph something like this: http://www.extremefinitism.com/zeta_fixed_value.png
Often the Casimir Effect is cited as a real-world example of where weird summation results like this -1/12 actually occur. This is all misinformation (or Fake News if you prefer). We are on a long and slippery road once we start to assume that if some mathematics appears to describe a physical effect, then that mathematics correctly models the physical reality.
Consider the ptolemaic model of the universe, where the earth was considered to be at the centre of the whole universe. The mathematics that described the path of the planets, sun and moon gave the correct answers and enabled their future positions to be predicted. But these objects were not really doing weird loop-the-loop paths around the planet earth, even though the maths appeared to work.
The value used in the derivation of the Casimir effect is the supposed sum of the cubes of natural numbers, which is claimed to be positive 1/120. Again this value is simply the limit of the area (on the graph of the respective partial sum expression) between -1 and 0. It has nothing to do with ‘infinity’.
Physicists have demonstrated the Casimir Effect using water waves (although alcohol works better than water). Only waves of a certain range of wavelengths can fit between the plates, but a wider range of wavelengths can occur outside of the two plates. There is a huge danger in assuming that ‘an infinite amount of different waves must be possible’. When the effect is produced using a fluid like water or alcohol, these fluids have a finite number of molecules and during the experiment they produce a finite number of waves. The effect provides no basis for the assumption that actual infinities must exist in the real world, or even that the maths is somehow using ‘infinity’; it isn’t.
I have a video about this minus one twelfth topic on YouTube, but I won’t link to it here as that might be considered spammy.
I agree with Karma Peny:
Maths can easily be misused: Like the misuses of infinity, since
inf * inf = inf, and inf * k = inf, if you divide both sides by inf
( you can’t and this is a misuse ),
you get inf/inf ( which is infinity, because infinity is indivisible, even by itself, ) = k. Now, let k = -1/12.
Keep in mind that math is a simple and elegant tool to understand the universe, and if setting k = -1/12 gives you a new tool for understanding quantum chromodynamics, then by all means…
Regarding the 1 – 2 + 3 – 4 + … =1/4 series, I wonder what is the case when the terms are grouped as below.
1 – 2 + 3 – 4 + 5 – 6 + ….
=(1 – 2) + (3 – 4) + (5 – 6) + ….
=(-1) + (-1) + (-1) + ….
=-(1 + 1 + 1 + …)
=1/4 ?
This is a contradiction if 1 + 1 + 1 + … diverges to infinity. But where is the fallacious reasoning?